5.4. Критерий согласия Пирсона

О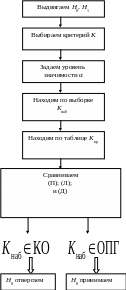 . 1. Критерий проверки гипотезы о предполагаемом законе распределения называется критерием согласия. Структурная схема алгоритма проверки статистических гипотез представлена на рис. 18.

Рис. 18. Структурная схема алгоритма проверки статистических гипотез

Критерий согласия Пирсона или критерий согласия χ² (хи-квадрат) является важным критерием математической статистики. Он может употребляться при решении задач инженерно-техно-логического, биологического, экономического и другого характера.

Суть метода основана на сравнении эмпирических и теоретических частот. Критерий Пирсона отвечает на вопрос: случайно ли расхождение этих частот.

Мерой сравнения (критерием согласия) служит величина

,

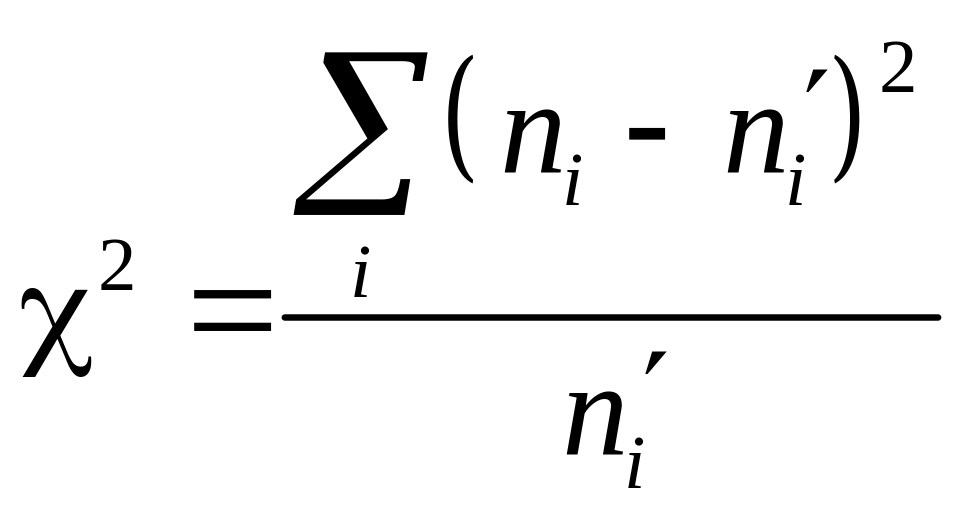где n_i – эмпирические или наблюдаемые частоты (частота попадания значений выборки в i-ый интервал); – теоретические или ожидаемые частоты (частота попадания с.в., распределенной по предполагаемому закону, в i-ый интервал).

Очевидно, чем меньше разница между n_i и , тем меньше величина критерия χ².

Методика расчета теоретических частот

Пусть Н₀ – «ГС имеет нормальное распределение». Центри-руем и нормируем с.в. Х, вводя в рассмотрение теоретическую с.в.

,

значения которой вычисляются по формулам

,

при этом полагают .

Тогда вероятность попадания с.в. Z в i-ый интервал согласно предположению о нормальном распределении ГС равна

,

где Ф(z) – интегральная функция Лапласа (см. табл. П. 1).

Теоретические частоты вычисляются по формуле

,

где n – объем выборки.

Для контроля правильности вычислений используют условие

.

О. 2. Величина K = L – 1 – r называется числом степеней свободы. Здесь L – количество интервалов разбиения; r – количество параметров предполагаемого распределения.

Например, если проверяется гипотеза о том, что с.в. распределена по показательному закону (с одним параметром λ), то r = 1, если же проверяется гипотеза о нормальном распределении с.в. (с двумя параметрами a и σ), то r = 2.

По числу степеней свободы K (поскольку нормальное распределение двухпараметрическое, то число степеней свободы равно K = L – 3) и по заданному уровню значимости α для правосторонней критической области определяют (см. табл. П. 4).

Вычисляем (расчетную таблицу см. в образце выполнения типового расчета).

Тогда при выполнении условия гипотеза Н₀ принимается (говорят, что данные выборки не противоречат выдвинутой гипотезе), а при выполнении условия гипотеза Н₀ отвергается (говорят, что данные выборки не подтверждают выдвинутой гипотезы).

Алгоритм проверки гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона представлен на рис. 19.

5.5. Решение типовых задач (типового расчета)

Дана выборка объема n = 150. Для заданного массива чисел провести следующую статистическую обработку:

1. Построить интервальный статистический ряд из 11 интервалов.

2. Построить гистограмму и эмпирическую функцию плотности распределения.

3. Используя метод условных вариант, найти точечные статистические оценки: выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную выборочную дисперсию, исправленное выборочное среднее квадратическое отклонение, асимметрию и эксцесс.

Р

нет да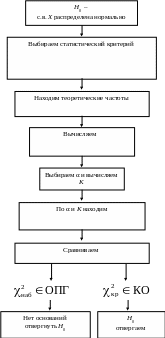

ис. 19. Алгоритм проверки гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона

4. Найти и построить эмпирическую функцию распределения.

5. При уровне надежности 0,99 найти доверительные интервалы для математического ожидания генеральной совокупности при неизвестном среднем квадратическом отклонении и для среднего квадратического отклонения нормальной генеральной совокуп-ности.

6. Проверить гипотезу о нормальном распределении генеральной совокупности по критерию Пирсона с уровнем значимости 0,05.

Дана выборка значений с.в. Y:

1) 259,829	26) 253,778	51) 270,081	76) 268,955	101) 296,778	126) 263,433
2) 267,64	27) 244,805	52) 262,457	77) 238,353	102) 268,218	127) 252,37
3) 312,899	28) 252,102	53) 271,951	78) 230,743	103) 246,303	128) 272,148
4) 272,813	29) 281,438	54) 252,563	79) 265,646	104) 264,015	129) 264,112
5) 261,48	30) 256,436	55) 278,693	80) 248,897	105) 246,601	130) 259,992
6) 254,038	31) 253,982	56) 265,864	81) 253,174	106) 290,478	131) 270,929
7) 293,042	32) 280,877	57) 299,315	82) 271,471	107) 279,664	132) 267,557
8) 269,126	33) 279,755	58) 290,393	83) 272,24	108) 291,862	133) 270,364
9) 252,017	34) 283,098	59) 271,525	84) 275,873	109) 288,168	134) 270,38
10) 265,058	35) 288,484	60) 254,038	85) 285,553	110) 286,977	135) 257,347
11) 277,691	36) 293,042	61) 268,573	86) 268,041	111) 284,058	136) 301,452
12) 263,848	37) 296,622	62) 269,352	87) 261,765	112) 306,836	137) 303,342
13) 266,344	38) 278,231	63) 269,864	88) 269,778	113) 279,049	138) 287,113
14) 264,323	39) 265,336	64) 267,378	89) 257,85	114) 263,771	139) 272,685
15) 256,36	40) 270,418	65) 257,906	90) 297,077	115) 263,101	140) 276,359
16) 283,28	41) 252,985	66) 262,670	91) 300,167	116) 256,203	141) 256,993
17) 272,843	42) 278,86	67) 258,501	92) 295,17	117) 292,483	142) 246,415
18) 266,4	43) 278,146	68) 259,151	93) 276,384	118) 270,714	143) 257,282
19) 264,603	44) 257,155	69) 270,366	94) 257,538	119) 266,169	144) 278,083
20) 267,741	45) 273,997	70) 256,433	95) 255,497	120) 283,157	145) 264,89
21) 269,272	46) 257,56	71) 242,25	96) 266,39	121) 303,556	146) 252,727
22) 255,611	47) 252,481	72) 238,538	97) 252,693	122) 300,772	147) 282,907
23) 266,835	48) 253,816	73) 279,923	98) 248,381	123) 308,472	148) 293,569
24) 259,814	49) 261,213	74) 271,084	99) 259,567	124) 306,441	149) 275,939
25) 270,127	50) 250,429	75) 270,526	100) 306,935	125) 286,887	150) 259,687

I. Построение интервального статистического ряда

1. Упорядочим данный числовой массив, т. е. построим вариационный ряд.

2. Число задаваемых интервалов K = 11.

3. Находим наименьшую и наибольшую варианты в выборке

Y_min = 230,743, Y_max = 312,899.

4. Находим длину интервала статистического ряда

.

5. Вычисляем крайние границы статистического ряда

;

.

Следующие границы подсчитываем по итерационной формуле

y_i+1 = y_i + Y,

считая у_лев = у₀.

Столбцы 1, 2, 3 табл. 1 и представляют интервальный статистический ряд для данной с.в. Y.

А столбцы 1, 3, 4 могут рассматриваться как дискретный статистический ряд. В силу плотности значений с.в. Y здесь середина интервала может считаться общим для всех вариант данного интервала.

Таблица 1

№	(yi; yi+1)	ni		ui	uini
1	2	3	4	5	6	7	8	9
1	226,6352; 234,8508	1	230,743	– 5	– 5	25	– 125	625
2	234,8508; 243,0664	3	238,9586	– 4	– 12	48	– 192	768
3	243,0664; 251,282	7	247,1742	– 3	– 21	63	– 189	567
4	251,282; 259,4976	30	255,3898	– 2	– 60	120	– 240	480
5	259,4976; 267,7132	31	263,6054	– 1	– 31	31	– 31	31
6	267,7132; 275,9288	30	271,821	0	0	0	0	0
7	275,9288; 284,1444	20	280,0366	1	20	20	20	20
8	284,1444; 292,36	9	288,2522	2	18	36	72	144
9	292,36; 300,5756	10	269,4618	3	30	90	270	810

Окончание табл. 1

1	2	3	4	5	6	7	8	9
10	300,5756; 308,7912	8	304,6834	4	32	128	512	2048
11	308,7912; 317,0068	1	312,899	5	5	25	125	625
		150			– 24	586	222	6118

II. Построение гистограммы частот и эмпирической функции плотности распределения

Для интервального статистического ряда построим его геометрический аналог – гистограмму частот, по которой строится эмпирическая функция плотности распределения.

Гистограмма частот и эмпирическая функция плотности распределения представлены на рис. 20.

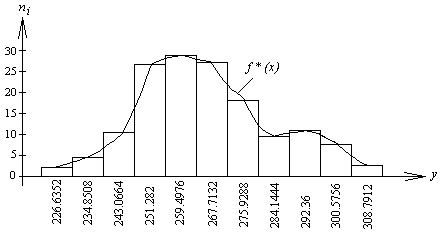
Рис. 20. Гистограмма частот и эмпирическая функция плотности распределения

III. Расчет точечных статистических оценок

Для удобства расчетов перейдем к условным вариантам

,

где с – «ложный нуль» – выбирается из середины статистического ряда и в нашем случае c = 271,821.

1. Вычислим выборочную среднюю по формуле

.

Получим

.

2. Вычислим выборочную дисперсию

,

где – условные статистические моменты k-го порядка.

Вычислим статистические моменты 1, 2, 3 и 4-го порядков:

, ,

, .

Тогда выборочная дисперсия равна

.

Вычислим исправленную выборочную дисперсию

.

3. Вычислим выборочное среднее квадратическое отклонение по формуле

.

Тогда

.

Исправленное СКО вычислим по формуле

.

Получим

.

4. Найдем числовые характеристики деформации.

Асимметрию найдем по формуле

,

где ; m₃ – центральный эмпирический момент 3-го порядка, m₃ = = .

Статистические моменты были вычислены ранее. Тогда центральный эмпирический момент 3-го порядка равен

.

Вычислим асимметрию

.

Эксцесс найдем по формуле

,

где ; m₄ – центральный эмпирический момент 4-го порядка, m₄ = = .

Статистические моменты были вычислены ранее. Тогда центральный эмпирический момент 4-го порядка равен

.

Вычислим эксцесс

.

IV. Эмпирическая функция распределения

По определению

График эмпирической функции распределения представлен на рис. 21.

1

149/150

141/150

131/150

122/150

102/150

72/150

41/150

11/150

4/150

1/150

Рис. 21. График эмпирической функции распределения

V. Расчет доверительных интервалов

1. Доверительный интервал для математического ожидания.

Выбираем формулу для случая, когда σ неизвестно:

.

А. Задаем надежность γ = 0,95.

Находим по табл. П. 2

t_γ = t(0,95,150) = 1,96.

Тогда

;

;

.

Здесь длина интервала |а – b| = 2,599.

Б. Пусть теперь надежность γ = 0,99.

Соответственно, t_γ = t(0,99,150) = 2,576.

Тогда доверительный интервал примет вид

;

;

.

Видим, что с увеличением надежности интервал расширяется. Здесь длина интервала |a – b| = 3,416.

2. Доверительные интервалы для среднего квадратического отклонения.

Доверительные интервалы для СКО вычисляются по формуле .

А. Выбираем надежность γ = 0,95, тогда значение q = q(0,95,150) = 0,115 (табл. П. 3)

.

Б. При надежности γ = 0,99 получаем значение q = q(0,99,150) = 0,16

и

.

Вычислив длины интервалов, опять убеждаемся в том, что чем выше надежность, тем шире интервал.

VI. Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона

Судя по гистограмме и значениям асимметрии и эксцесса (близким к нулю), можно выдвинуть гипотезу Н₀ – «ГС распределена нормально». Проверим эту гипотезу по критерию Пирсона.

Пересчитаем границы интервалов

.

В силу того что нормальное распределение охватывает всю числовую ось, полагают

, .

Все промежуточные значения вычисляются по указанной формуле:

;

;

;

;

;

;

;

;

;

.

Вероятность попадания величины в i-ый интервал рассчитывается по формуле

,

где – интегральная функция Лапласа (см. табл. П. 1).

Теоретические частоты рассчитываются по формуле

.

Составим расчетную таблицу (табл. 2) для наблюдаемого значения критерия Пирсона.

Таким образом, наблюдаемое значение критерия .

Таблица 2

zi	zi+1	Ф(zi)	Ф(zi+1)	pi
	–2,203	–0,5	–0,4861	0,0139	2	–1	0,5
–2,203	–1,695	–0,4861	–0,4549	0,0311	5	–2	0,8
–1,695	–1,188	–0,4549	–0,383	0,0719	11	–4	1,455
–1,188	–0,68	–0,383	–0,2517	0,1313	20	10	5
–0,68	–0,173	–0,2517	–0,0694	0,1822	27	4	0,593
–0,173	0,335	–0,0694	0,1312	0,2006	30	0	0
0,335	0,843	0,1312	0,3009	0,1697	25	–5	1
0,843	1,35	0,3009	0,4115	0,1106	17	–8	3,765
1,35	1,858	0,4115	0,4686	0,0571	9	1	0,111
1,858	2,365	0,4686	0,491	0,0224	3	5	8,333
2,365		0,491	0,5	0,009	1	0	0
				1	150		21,577

По уровню значимости и числу степеней свободы (S – количество интервалов) находим критическое значение критерия (табл. П. 4)

.

Поскольку , следовательно, гипотеза о нормальном распределении ГС по критерию Пирсона отвергается.