4. Статистические оценки параметров генеральной совокупности и их классификация

Пусть в распоряжении исследователя имеются данные выборки. Очевидно, что в иной ситуации выборка может выглядеть по-другому и разные выборки будут давать разные результаты изучаемого параметра. Следовательно, нельзя говорить о том, что с помощью выборки находят истинный параметр генеральной совокупности, и можно утверждать, что найдено приближенное его значение или оценка.

О. 1. Статистической оценкой неизвестного параметра ГС  называют функцию от наблюдаемых случайных величин значений выборки, построенную по тому же закону, что и оцениваемый параметр ГС.

Пусть  – неизвестный параметр. Тогда есть статистическая оценка параметра.

Для того чтобы найденная по выборке оценка была «хорошей», необходимо, чтобы она была

• несмещенной;

• эффективной;

• состоятельной.

О. 2. Оценка называется несмещенной, если , смещенной, если , т. е. оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, в противном случае оценка называется смещенной.

Возможные значения могут быть сильно рассеяны вокруг параметра .

О. 3. Оценка называется эффективной, если среди всех оценок она обладает наименьшей дисперсией, т. е.

.

О. 4. Оценка называется состоятельной, если при увеличении объема выборки вероятность того, что оценка мало отличается от истинного значения, приближается к единице, т.е.

.

О. 5. Оценки, представленные одним числовым значением, называются точечными.

О. 6. Оценки, представленные двумя числами – концами интервалов, называются интервальными.

Статистические оценки параметров ГС, с одной стороны, получаются из отдельных элементов ГС, а с другой – позволяют сформировать представление о всей ГС (рис. 13).

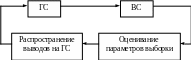
Рис. 13. Схема изучения ГС

4.1. Точечные оценки

Прежде чем рассматривать оценки, необходимо знать, как строится сам параметр.

О. 1. Среднее арифметическое значений признака ГС называется генеральной средней (х_г).

Формулы для вычисления х_г следующие:

, если x_i различны.

, если данные сгруппированы (x_i имеют частоты N_i).

Пусть для изучения ГС извлечена выборка объема n.

О. 2. Среднее арифметическое значений признака выборочной совокупности (выборки) называется выборочной средней ( ).

Для дискретного ряда

, если все x_i различны,

или , если данные сгруппированы (x_i имеют частоты n_i).

Для интервального ряда

.

Выборочную среднюю принимают в качестве оценки для ГС, и эта оценка является несмещенной, т. е. . Она является также и состоятельной. При увеличении объема выборки , и для разных выборок значения примерно будут равны между собой.

О. 3. Генеральной дисперсией (D_г) называется среднее арифметическое квадратов отклонений значений признака ГС от генеральной средней.

Формулы для вычисления D_г следующие:

, если x_i различны;

, если значения сгруппированы (x_i имеют частоты N_i).

О. 4. Генеральным средним квадратическим отклонением (σ_г) называется корень квадратный из генеральной дисперсии:

.

Для выборки вводят аналогичные понятия, формулы которых определяются по тем же законам.

О. 5. Выборочной дисперсией (D_в) называется среднее арифметическое квадратов отклонений наблюдаемых значений от среднего значения.

Для дискретного ряда

, если x_i различны,

или

, если данные сгруппированы (x_i имеют частоты n_i).

Для интервального ряда

, где – середины i-х интервалов.

О. 6. Выборочным средним квадратическим отклонением (σ_в) называется корень квадратный из выборочной дисперсии:

.

Вычисление D_в можно упростить:

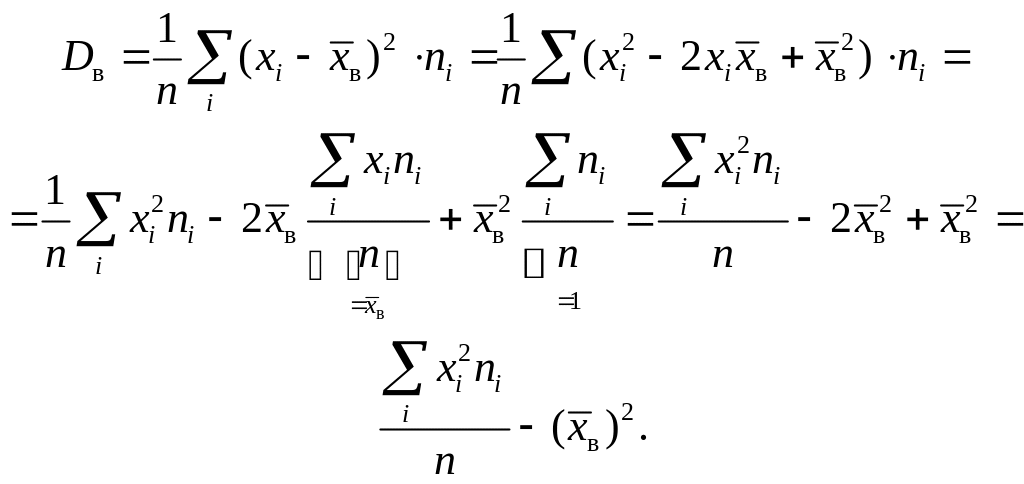
Итак,

Примечание. Эта формула может быть использована для контроля верности вычислений.

К сожалению, D является смещенной оценкой, т. к. .

И хотя в некоторых случаях ее можно использовать, для более тонких исследований вводят понятие несмещенной или исправленной выборочной дисперсии ( ):

.

Выражение есть исправленное среднее квадратическое отклонение (СКО).

Способы вычисления точечных оценок

I. Если первоначальные варианты x_i большие числа, то для упрощения расчетов переходят к условным вариантам u_i, где , – «ложный» нуль, т. е. число, близкое к выборочной средней, выбирается «на глаз» в середине ряда.

В этом случае .

Дисперсия при этом не изменится. Действительно, по свойствам дисперсии D(x) = D(u + c) = D(u). Тогда

.

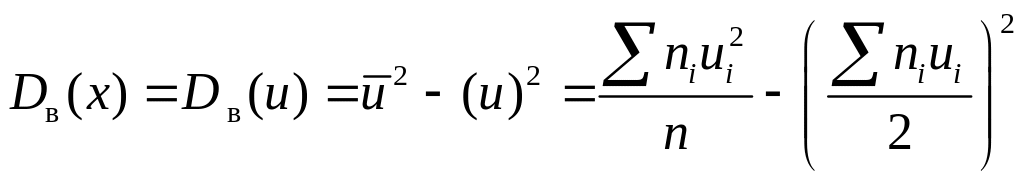II. Для равномерного ряда удобно использовать метод произведений, когда выборочная средняя и выборочная дисперсия находятся по формулам

,

,

где u_i = (x_i – C)/Δx – условная варианта; и D_в(u) – выборочная средняя и дисперсия этой варианты, вычисляемые по известным формулам (см. образец выполнения типового расчета, п. 5.5).