7.2. Однофакторный дисперсионный анализ Одинаковое число испытаний на всех уровнях

Пусть на количественный, нормально распределенный признак Х воздействует фактор F, который имеет р постоянных уровней. На каждом уровне произведено по q испытаний. Результаты наблюдений – числа (i – номер испытания, i = 1, 2, 3, …, q; j – номер уровня фактора, j = 1, 2, 3,…, р) – записывают в виде таблицы (табл. 4).

В последней строке табл. 4 вычислены средние значения измерений для каждого уровня.

Ставится задача: при уровне значимости  проверить нулевую гипотезу о равенстве групповых средних при допущении, что групповые генеральные дисперсии хотя и не известны, но одинаковы.

Таблица 4

Номер испытания	Уровни фактора
i			…
1			…
2			…
…	…	…	…	…
q			…
Групповая средняя			…

Для решения этой задачи вводятся следующие определения.

О. 1. Общей средней является величина, равная

.

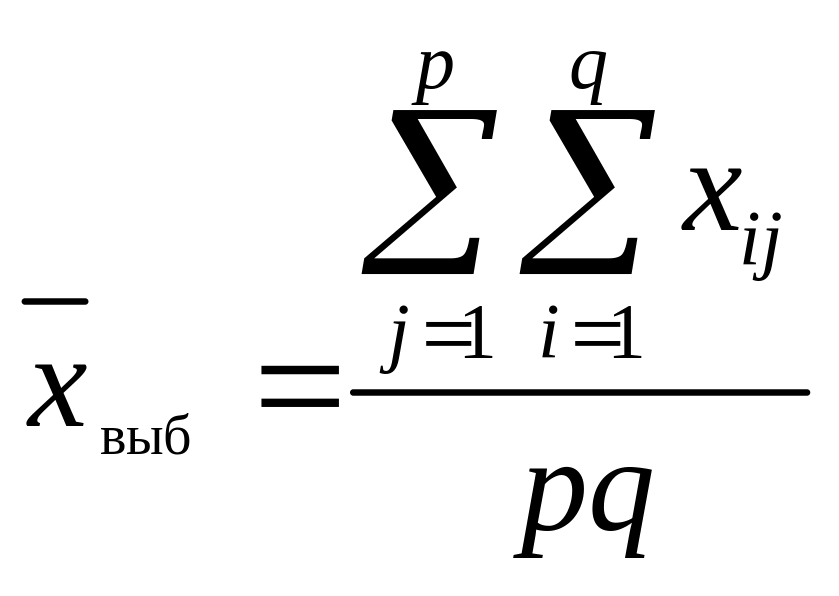О. 2. Общей суммой квадратов отклонений измеренных значений от общей средней называется выражение

.

О. 3. Факторной суммой квадратов отклонений групповых средних от общей средней называется выражение

.

О. 4. Остаточной суммой квадратов отклонений наблюдаемых значений от групповых средних является сумма

.

Примечание. Обычно остаточную сумму находят как разность общей и факторной сумм:

.

Полученная формула является основным тождеством дисперсионного анализа.

Выдвигаем гипотезу H₀: групповые средние равны. Конкурирующая гипотеза H₁: групповые средние не равны.

Для проверки нулевой гипотезы используем критерий Фишера-Снедекора, то есть случайную функцию :

,

где и являются несмещенными оценками соответствующих дисперсий, которые получаются делением сумм квадратов отклонений на соответствующее число степеней свободы:

, .

Число степеней свободы определяется как общее число наблюдений минус число связывающих их уравнений. Поэтому в первом случае число степеней свободы равно (р – 1), так как при его расчете используют р групповых средних, связанных между собой одним уравнением. А во втором случае число степеней свободы равно (pq – p) = p(q – 1), так как при его расчете используют все pq наблюдений, связанных между собой р уравнениями.

Затем по таблице распределения Фишера-Снедекора (табл. П. 6) по заданному уровню значимости  и числу степеней свободы и находим величину .

Если , то гипотеза о равенстве групповых средних отвергается (т. е. влияние фактора на количественный признак Х значимо).

Если , то гипотеза о равенстве групповых средних принимается (т. е. фактор на количественный признак Х не влияет).

Неодинаковое число испытаний на различных уровнях

Пусть на количественный, нормально распределенный признак Х воздействует фактор F, который имеет р постоянных уровней. Но на каждом уровне число испытаний различно (общее число испытаний ). Результаты наблюдений – числа (i – номер испытания, i = 1, 2, 3, …, q; j – номер уровня фактора, j = 1, 2, 3, …, р) – записывают в виде таблицы (табл. 5).

Таблица 5

Номер испытания	Уровни фактора
i			…
1			…
2	–		…
…	…	…	…	…
i		-	…	…
i + 1	…		…	–
…	…	…	…	…
q			…
Количество испытаний на i-ом уровне			…
Групповая средняя			…

Пусть результаты наблюдений составляют p независимых вы­борок (групп), полученных из p нормально распределенных ге­неральных совокупностей, которые имеют, вообще говоря, раз­личные средние и равные дисперсии.

Проверяется нулевая гипотеза Н₀ о равенстве групповых средних.

На практике такая задача возникает при исследовании влияния, которое оказывает изменение некоторого фактора на измеряемую величину. Например, если измерения проводятся на р различных приборах, то можно исследовать влияние фактора «прибор» на результаты измерений. В данном случае нас интересует вопрос, имеют ли различные приборы одну и ту же систематическую ошибку (гипотеза Н₀). При двух сериях наблюдений р = 2 для проверки гипотезы Н₀ используется критерий Стьюдента. Если , то для проверки гипотезы о равенстве р средних применяют однофакторный дисперсионный анализ, суть которого состоит в следующем.

Пусть результат наблюдения обозначает i-й элемент k-й выборки, i = 1, 2, …, q; k = 1, 2, …, p.

Обозначим усреднение по какому-либо индексу звездочкой

вместо индекса.

О. 1. Выборочным средним k-й выборки называется величина , вычисляемая по формуле

= .

О. 2. Общей средней называют величину

= ,

где n – общее число наблюдений, n = .

Общая сумма квадратов отклонений наблюдений от общего среднего может быть представлена так:

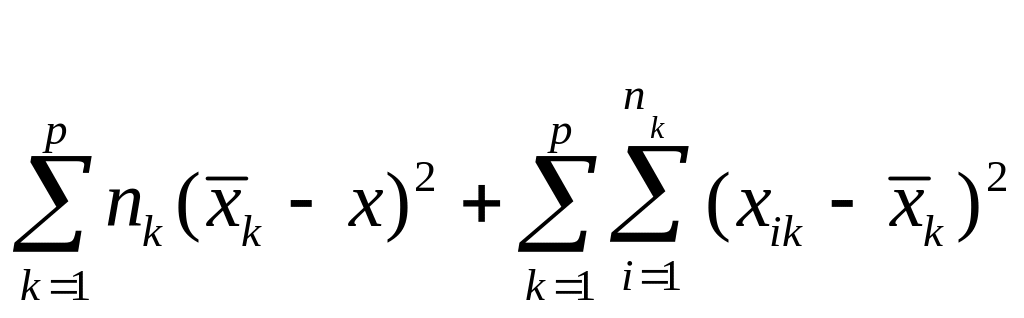) = . (1)

Формула (1) также представляет собой основное тождество дисперсионного анализа.

Если верна гипотеза Н₀, то статистики и явля­ются несмещенными оценками неизвестной дисперсии.

Оценка характеризует рассеяние групповых средних, а оценка – рассеяние внутри групп, которое обусловлено воздействием некоторой случайной величины (неучтенный фактор).

Если окажется меньше , то отсюда следует справедливость гипотезы о равенстве групповых средних.

В противном случае проверку нулевой гипотезы проводят по критерию Фишера-Снедекора, т. е. вычисляют :

.

Затем по таблице распределения Фишера-Снедекора (табл. П. 6) по заданному уровню значимости  и числу степеней свободы и находим величину .

Если , то гипотеза о равенстве групповых средних отвергается (т. е. влияние фактора на количественный признак Х значимо).

Если , то гипотеза о равенстве групповых средних принимается (т. е. фактор на количественный признак Х не влияет).

Примечание. На практике для расчетов сумм квадратов часто бывает более удобно использовать следующие формулы:

,

,

.

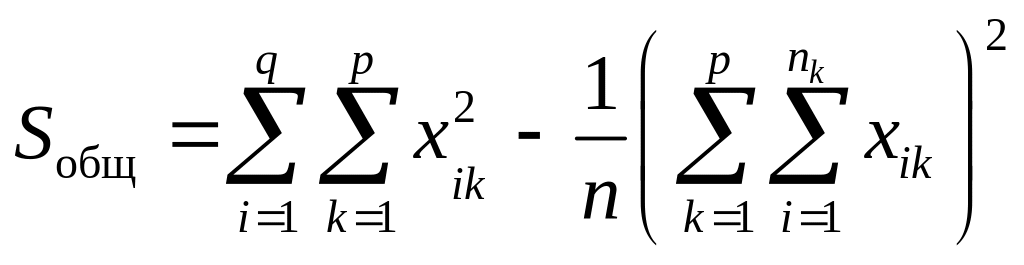Таким образом, сами средние, вообще говоря, находить не обязательно.