6. Элементы корреляционно-регрессионного анализа

Существуют разные типы зависимостей между случайными величинами X и Y, например, функциональная и статистическая (стохастическая).

О. 1. Связь признака Y с X называется функциональной (жестко детерминированной), если каждому возможному значению независимого признака X соответствует единственное значение зависимого признака Y, т. е. .

В реальной социально-экономической ситуации ввиду неполноты информации, как правило, нет указаний на характер функции, связывающей разные случайные величины. В этом случае между признаками может существовать стохастическая (вероятностная) связь.

О. 2. Зависимость величины Y от X называется стохастической или статистической, если каждому значению независимого признака X соответствует не одно, а множество значений переменной Y, причем заранее неизвестно, какое из них переменная Y примет при каждом конкретном значении Х.

О. 3. Корреляционная зависимость – зависимость случайных величин (признаков), при которой изменение статистического распределения одной случайной величины вызывает изменение среднего значения другой случайной величины.

Основной задачей корреляционного анализа является вопрос: существует ли между признаками X и Y корреляционная зависимость.

О. 4. Показатель тесноты связи между признаками (с.в.) X и Y

называется коэффициентом корреляции.

Примечание. Коэффициент корреляции . Знак коэффициента характеризует направление взаимосвязи, а абсолютная величина – степень тесноты рассматриваемой взаимосвязи. Причем если

X и Y не коррелированы;

связь между X и Y практически отсутствует;

корреляционная связь слабая;

корреляционная связь достаточно сильная (коэффициент корреляции значим);

высокая степень корреляционной зависимости (коэффициент корреляции значим);

наличие строгой функциональной связи, а не статистической.

Кроме того, значимость коэффициента корреляции можно выявить проверкой соответствующей гипотезы.

Если , то X и Y называются коррелированными.

О. 5. Функция , описывающая изменения среднего группового значения переменной Y при изменении значений x переменной X, называется функцией регрессии Y на X.

О. 6. График функции регрессии называется линией регрессии.

Основной задачей регрессионного анализа является определение типа связей между признаками X и Y.

Для двух ГС существуют следующие виды связей: линейная связь (представляется уравнениями первой степени) и криволинейная (представляется, например, степенной, гиперболической, показательной, логарифмической и другими функциями).

О. 7. Если обе линии регрессии Y на X и Х на Y – прямые, то корреляцию называют линейной.

Выборочные уравнения прямой линии регрессии имеют вид

Y на X ,

X на Y .

Здесь r_в – выборочный коэффициент корреляции, который определяется по формуле

,

где x, y – наблюдаемые варианты признаков X и Y; σ_x, σ_y – выборочные СКО; – выборочные средние; – частота пары вариант (x; y); n – объем выборки.

6.1. Решение типовых задач (типового расчета)

На 55 полей агропромышленного комплекса были внесены удобрения в разных количествах (с.в. Y, ц/га). После уборки хлеба была изучена урожайность каждого поля (параметр X, ц/га). Получена корреляционная таблица. Определить значение коэффициента корреляции, в случае его значимости найти выборочные уравнения прямых линий регрессии Y на X и X на Y. Построить эти линии на плоскости.

Y	X						ny
	65	95	125	155	185	215
30	5						5
40	4	12					16
50		8	5	4			17
60		1	5	7	2	1	15
70					1	1	2
nx	9	21	10	11	3	2	n = 55

Решение. Для удобства арифметических расчетов перейдем к условным вариантам u и v по формулам

, ,

где С₁ = 155 – «ложный нуль» для варианты u; С₂ = 50 – «ложный нуль» для варианты v; h₁ = 30, h₂ = 10 – длина интервала соответствующей варианты.

Составим корреляционную таблицу для условных вариант u и v.

v	u						nv
	–3	–2	–1	0	1	2
–2	5						5
–1	4	12					16
0		8	5	4			17
1		1	5	7	2	1	15
2					1	1	2
nu	9	21	10	11	3	2	n = 55

Найдем выборочные средние условных вариант u и v.

Выборочное среднее для варианты u находим по формуле

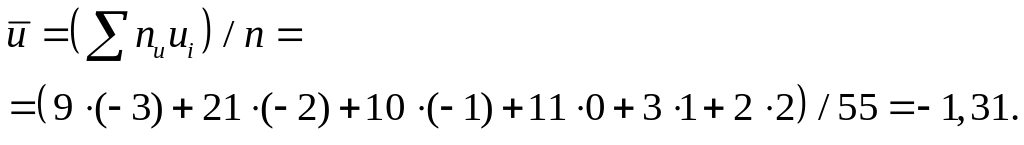
Найдем вспомогательные величины :

Найдем СКО для условных вариант:

Составим расчетную таблицу (табл. 3) для нахождения выборочного коэффициента корреляции.

Суммируя числа последнего столбца расчетной таблицы, находим

.

Для контроля вычислений находим сумму чисел последней строки:

.

Совпадение свидетельствует о правильности вычислений.