4.2 Метод множителей Лагранжа.
Другой способ определения условного экстремума осуществляется с построения вспомогательной функции Лагранжа, которая достигает max для тех же х1,х2,…,хn, что и целевая функция z.
Пусть решается задача определения условного экстремума функции z=f(x) при ограничении
φ(х)=0.
Составим функцию, которая называется функция Лагранжа
m
L(x)=f(x)+∑λiφi(x)
i=1
λi – постоянные множители (множитель Лагранжа).
Определение стационарных точек приводит к решению системы уравнений:
∂L(x)/ ∂Xj=0, j=1,2,…n.
∂L(x)/ ∂λi =0, i=1,2,…m. отсюда видно, что
L′λi(x)= φi(x)
Таким образом, задача нахождения условного экстремума функции z=f(x) сводится к нахождению локального экстремума функции L(x). Если стационарная точка найдена, то вопрос о существовании экстремума решается на основании достаточного условия экстремума.
Пример:
Найти наибольшее и наименьшее значения
функции z=9x12+4x22+x32-(3x12+2x22+x32)
при условии, что х1 х2 х3
удовлетворяют уравнению х12+х22+х32=1,
которое опр
еделяет
сферу единичного радиуса.
Согласно теореме Вейерштрасса, функция достигает на этой сфере свое наибольшее и наименьшее значение. Находим условный глобальный экстремум. Запишем уравнение связи в виде: х12+х22+х32-1=0;
Составим функцию Лагранжа:
L=9x21+4x22+x23-(3x21+2x22+x23)+λ(x21+x22+x23-1)
Найдем частные производные этой функции по х1, x2, x3, λ и приравняем их к 0.
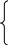
L′(x1)=х1((9+λ)-6(3 х12+2х22+х32))=0
L′(x2)=х2((4+λ)-4(3 х12+2х22+х32))=0
L′(x3)=х3((1+λ)-2(3 х12+2х22+х32))=0
Lλ′= х12+2х22+х32)) =1
Решая систему, получим стационарные точки(6 точек), в которых найдем значения функции z наибольшее=1 и z наименьшее=0
Однако применение классических методов в исследовании операций весьма ограничено, так как задача определения условного экстремума функции n переменных весьма трудоемка.
Поэтому разработаны приближенные методы решения нелинейных задач программирования, например, для выпуклых(вогнутых) функций.
5. Методы направленного поиска экстремумов.
Это пошаговые методы, на каждом шаге используется информация предыдущих шагов.
5.1 Методы определения экстремума унимодальной функции.
Унимодальная функция – функция, в интервале исследования имеющая только один экстремум.
А) Методы определения экстремума функции одной переменной.
И
дея
методов:
На каждом шаге выбирается 2 точки X1 и X2 в них определяются значения целевой функции, они сравниваются.
На рис. 1 f(X1)< f(X2), тогда из дальнейшего рассмотрения удаляется интервал [a, X1], т.к. там не будет экстремума.
На рис. 2 f(X1)> f(X2), тогда в интервале [X2, b] не может быть экстремума, если функция унимодальная.
На рис. 3 f(X1)= f(X2), тогда исключаются [a, X1] и [X2, b].
Б)Метод половинного деления (дихотомии).
Дана целевая функция, она унимодальна.
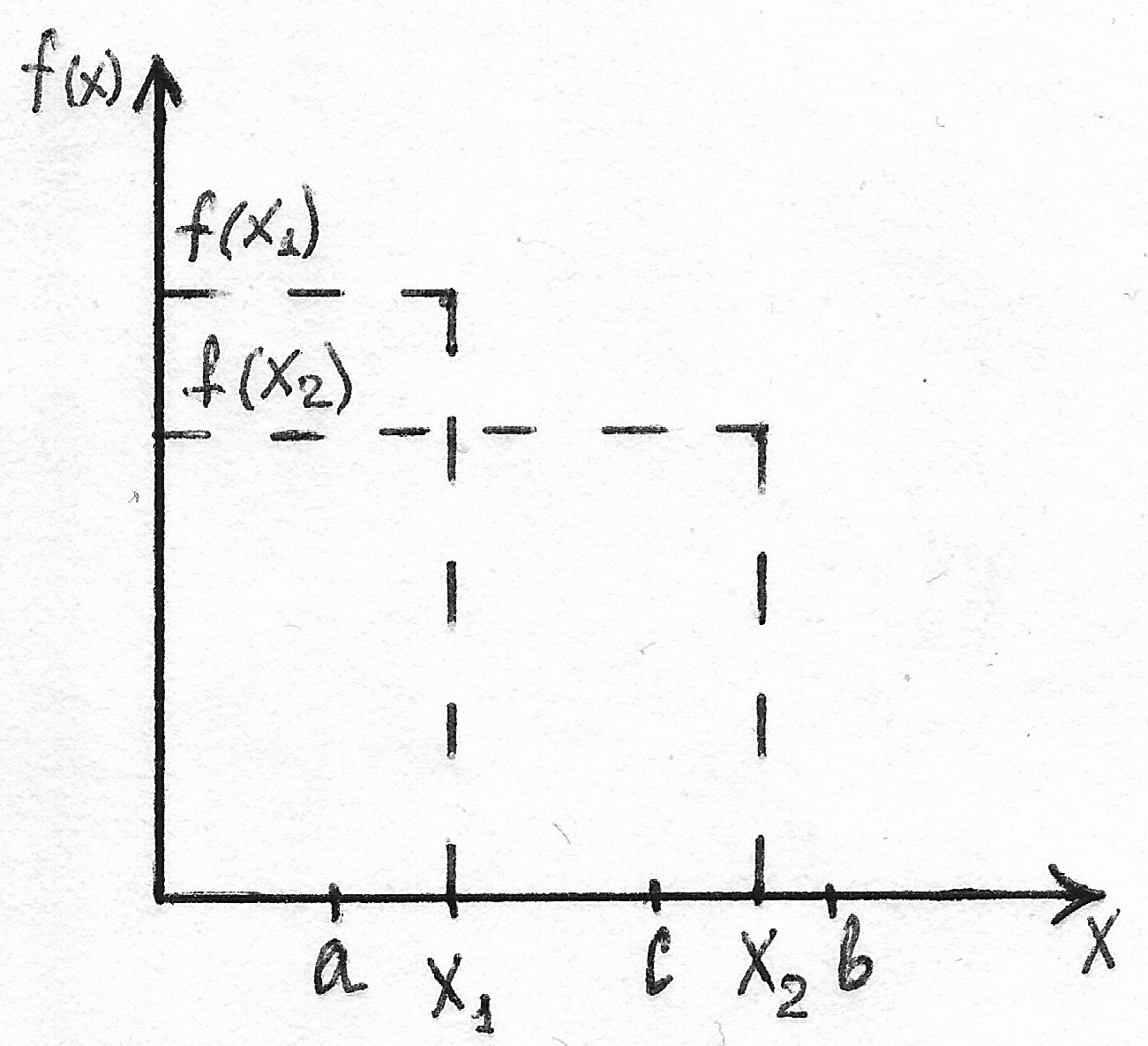
1. Если область изменения переменной неограниченна, то ее надо ограничить.
2. Интервал исследования делится пополам. Выбирается точность получения результата (интервал, внутри которого будет находится экстремум).
3. Заданный интервал делится пополам ∆Х/2, полученные величины откладываются от т. С влево и вправо. Получаем две точки X1 и X2.
4. В т. X1 и X2 вычисляется значение целевой функции.
5. Затем, используя свойство унимодальности целевой функции удалить из рассмотрения один из полученных интервалов и перейти на шаг 2.
В) Метод Фибоначчи.
В основе метода лежат числа Фибоначчи.
-
N
0
1
2
3
4
5
6
FN
1
1
2
3
5
8
13
N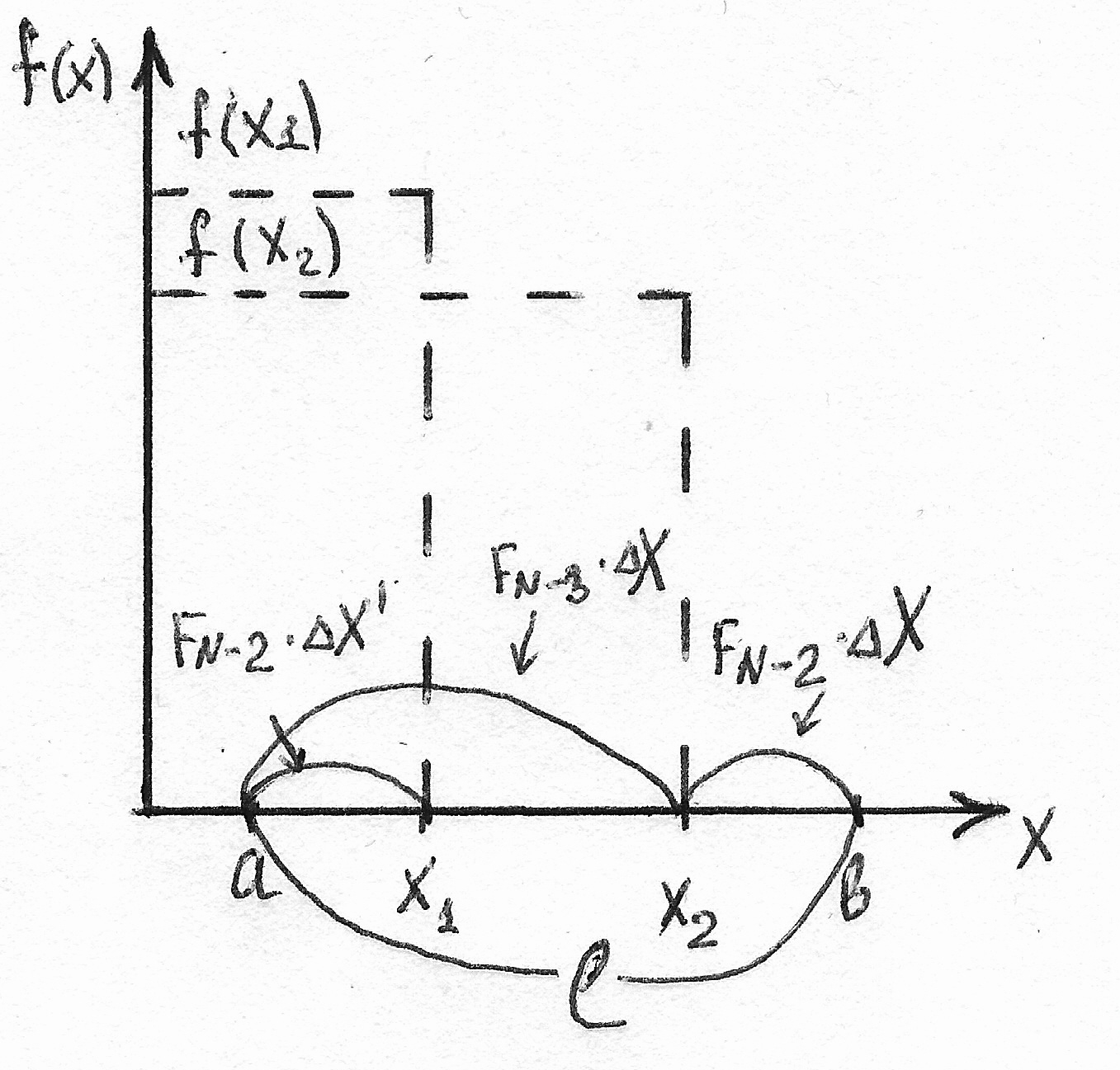
– порядковый номер;
F0= F1=1; FN= FN+1+ FN-2
Задана целевая функция f(X) и точность ∆Х.
Алгоритм метода.
1. Находится некоторое число F=l/∆Х, допустим F′ = 10(9)
2. Выбирается ближайшее наибольшее число Фибоначчи (FN = 13, N = 6)
3. Находится новая точность получения результата ∆Х′ = l/FN.
4. Зафиксировать 2 точки X1 и X2 следующим образом:
X1 = а + FN-2 * ∆Х’
X2 = b - FN-2 * ∆Х’
5.Вычисляется значения f(X1) и f(X2).
6. Используя свойство унимодальности – удалить из дальнейшего рассмотрения один из интервалов, в данном случае [X2, b].
Переход к новому циклу:
Анализируется интервал [a, X2]. От его концов откладываются новые точки X3 и X4. Их величина FN-3 * ∆Х’ (∆Х′ – то же порядковое число Фибоначчи ↓ на 1)
Причем из двух точек, полученных на каждой следующей итерации – одна известна, то есть нужно вычислить значение целевой функции только в одной оставшейся неизвестной точке.
Преимущество метода:
Нет необходимости вычислять два новых значения Х, а только одно значение аргумента и целевой функции. Метод Фибоначчи работает быстрее метода дихотомии.
Недостаток метода:
Подготовительная работа по заготовке таблиц Фибоначчи.
Г) Метод золотого сечения.
Задана целевая функция f(X), ограничения [a,b], точность получения результата ∆Х.
Если выполняется условие аb/ас=ас/ cb, то это золотое сечение.
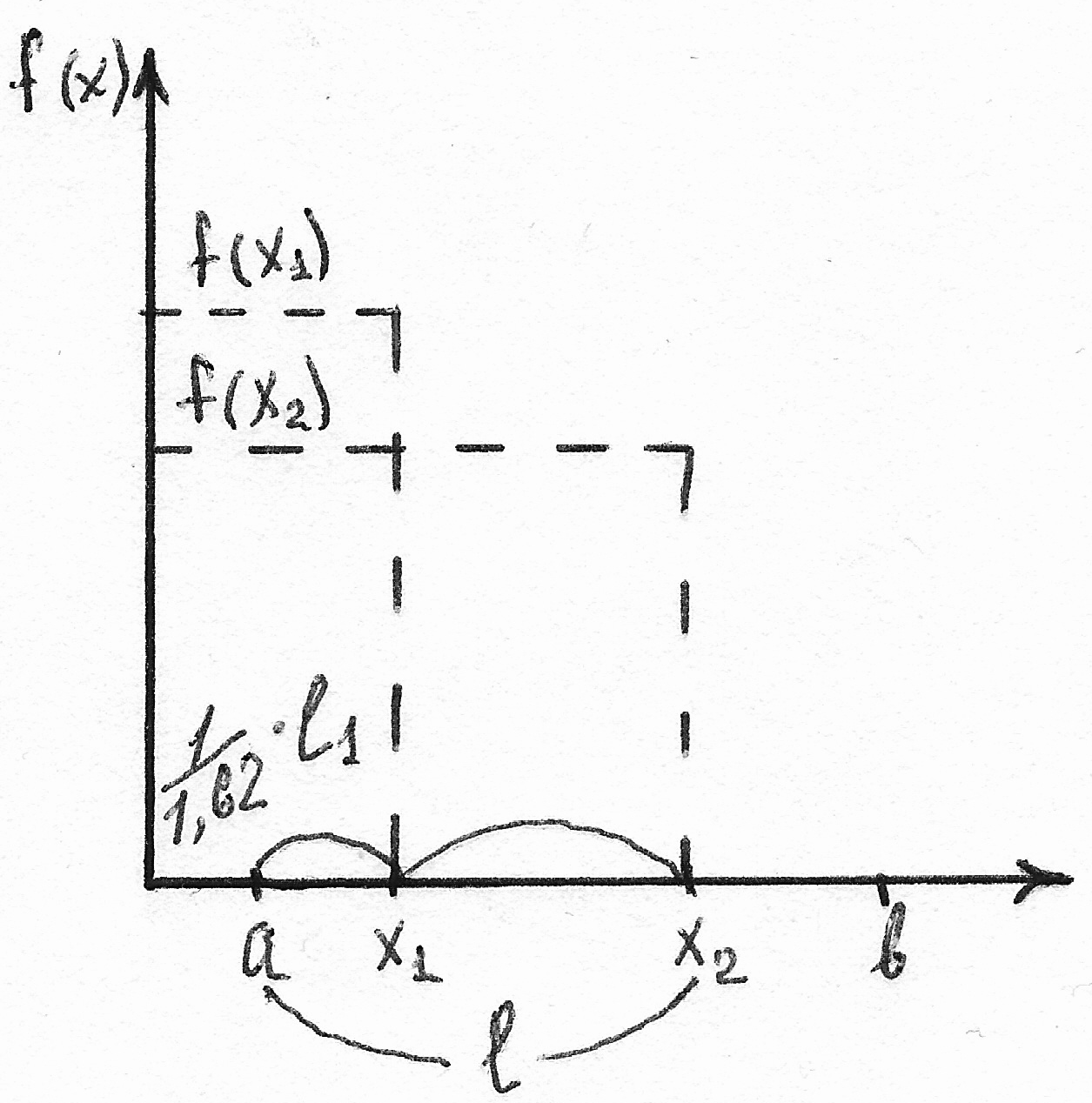
1) от концов интервала l откладываем интервалы aX2= bX1 = (1/1,62)∙l получаем точки X1 и X2.
2) определяются значения f(X1) и f(X2).
3)используя свойство унимодальности, удалить из рассмотрения один из крайних отрезков (в случае поиска max - [X2, b]). Остался интервал [a, X2] длинойl1. От его концов откладываются отрезки длиной (1/1,62)∙ l1. При этом одна из точек совпадает с одной из точек, оставшейся от предыдущей итерации.