4. Нелинейное программирование.

Во многих экономических моделях исследования зависимости между постоянными и переменными факторами не всегда оказываются линейными. В этом случае возникает задача нелинейного программирования. В нелинейном программировании существует несколько методов определения экстремумов. Основным из них является:

- классические методы оптимизации

4.1Классические методы оптимизации.

Различают локальные, глобальные и условные экстремумы.

а) Локальный экстремум.

Необходимые условия экстремума: если в точке х* функция z=f(x) имеет экстремум, то частные производные в этой точке равны 0.

fx_i(x*)=0, i = 1,2..n ( количество переменных).

Точка х* , в которой все частные производные функции z=f(x) равны 0, называется стационарной точкой.

Достаточные условия экстремума:

Для функции 2-х переменных z=f(x₁,x₂) cсуществуют 4 частные производные II порядка, из них две смешанные производные равны.

f′′х₁²(x₁,x₂);

f′′х₁х₂(x₁,x₂);

f′′х₂х₁(x₁,x₂);

f′′х₂²(x₁,x₂);

Найдем значения частных производных II порядка в стационарной точке х⁰(х₁⁰,х₂⁰)

а₁₁=f′′х₁²(х⁰)

а₁₂=f′′х₁х₂(х⁰)

а₂₁=f′′х₂х₁(х⁰)

а₂₂= f′′х²₂(х⁰)

Составим определитель, составленный из а_ij

∆= а₁₁ а₁₂ =а₁₁а₂₂-а₂₁а₁₂

а₂₁ а₂₂

Тогда достаточные условия экстремума функции 2х переменных имеют вид:

а)Если ∆>0 и а₁₁<0 (а₂₂<0), то функция в точке х⁰ имеет max.

Если ∆>0 и а₁₁>0 (а₂₂>0), то функция в точке х⁰ имеет min.

б)Если ∆<0, то экстремума нет.

в)Если ∆=0, то вопрос об экстремуме остается открытым.

Пример: Исследовать на экстремум функцию

Z=x₁⁴+x₂⁴-x₁²-2x₁x₂-x₂²

Находим частные производные:

Z ^′(x₁)= 4x₁³- 2x₁-2x₂

( * )

Z ^′(x₂) = 4x₂³- 2x₁-2x₂

Приравниваем частные производные к 0

4x₁³- 2x₁-2x₂=0 (1)

4x₂³- 2x₁-2x₂=0 (2)

Вычитая из (1)-(2) получим 4x₁³-4x₂³ =0 х₁=х₂ из (1) x₁³-x₁=0, х₁=0 и х₁= ±1

Имеем 3 стационарные точки х¹=(0,0), х²=(1,1),х³=(-1,-1)

Найдем вторые частные производные, используя(*)

Z^″ x₁²=(4x₁³- 2x₁-2x₂)^′_х1 =12x₁²-2

Z^″ x₁x₂=(4x₁³- 2x₁-2x₂)^′ _x2 = -2

Z^″ x₂x₁=(4x₁³- 2x₁-2x₂)^′ _x3 = -2

Z^″x₂ ² =(4x₁³- 2x₁-2x₂)^′_x4 = 12x₂ -2

В т.x^′1=(0,0), a₁₁= -2, a₁₂= a₂₁= -2 , a₂₂= -2

∆ = -2 -2 =0

-2 -2

Вопрос об экстремумах остается открытым (такая точка называется седловиной)

Вт. x^′2=(1,1) и В т x³=(-1,-1)

a₁₁= 10, a₁₂= a₂₁= -2 , a₂₂= 10

∆ = 10 -2 =96

-2 10

функция в этих точках имеет min, так как ∆>0, a₁₁>0 z_min= 1⁴+1⁴-1²-2∙1∙1-1²= -2

б)Глобальный экстремум (наибольшее, наименьшее значение функции).

Если область D замкнута и ограничена, то дифференцируемая функция z=f(x) достигает в этой области своего наибольшего и наименьшего значения в стационарной точке или в граничной точке области (теорема Вейерштрасса) следовательно, чтобы найти глобальный экстремум функции z в области D необходимо:

1)Найти все стационарные точки внутри области D и вычислить функции в них.

2)Исследовать функции на экстремум на границе области D.

3)Сравнить значения функции, полученные в пункте 1 и 2. Наибольшее или наименьшее из этих чисел и будет глобальным экстремумом.

в)Условный экстремум.

Пусть необходимо найти экстремум функции z=f(х₁,х₂,…,х_n) при условии, что эти переменные (х₁,х₂,…,х_n) удовлетворяют уравнению φ(х₁,х₂,…,х_n)=0, которое называется уравнением связи. Говорят, что в точке х⁰(х⁰₁,х⁰₂,…,х⁰_n), удовлетворяющему уравнению связи, функция z=f(x) имеет условный max (min), если f(х⁰)≥ f(x) (f(х⁰)≤ f(x)) имеет место для всех точек х, координаты которых удовлетворяют уравнению связи.

Пример.

Дана производственная функция z=x₁²x₂²(4-x₁-x₂) (1).

Цены С₁=1, С₂=2 и издержки b=4.

Необходимо найти х₁ и х₂, удовлетворяющие уравнению х₁+2х₂=4 (2) (уравнение связи) превращающее производственную функцию (1) в max.

x₂

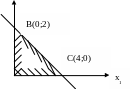
Уравнение (2) и условие неотрицательности на плоскости х₁Ох₂ образуют замкнутую ограниченную област. (см. рис.)

Согласно теореме Вейерштрасса max функции может быть достигнут либо внутри этого отрезка , либо в граничных точках А(4;0) и В(0;2).Следовательно необходимо найти условный экстремум функции (1), если уравнение связи(2).

Из (2) находим:

х₁=4-2х₂ тогда z=(4-2х₂)²x₂(4-4+2x₂-x₂), z=4(2-х₂)²x₂²

Найдем глобальный экстремум z′=16(2-x₂)x₂(1-x₂)=0, стационарная точка x₂=0; x₂=1; x₂=2; значение функций в этих точках z(0)=0; z(1)=4; z(2)=0;

Максимальный объем производства z_max=4 единицы, достигается при условии, что затраты х₁=2 и х₂ = 1 ед.