3.7.2 Распределительный метод нахождения оптимального плана тз

Выводы из 3.7.1 по существу являются алгоритмом распределительного метода для нахождения оптимального плана ТЗ.

Рассмотрим этот алгоритм на примере:

bj ai	22	34	41	20
31	10 22	7 9	6	8
48	5	6 25	5 23	4
38	8	7	6 18	7 20

1. Расставим опорный план методом северо-западного угла и найдем стоимость перевозок при данном первоначальном плане.

Z₀^с-з=10*22+7*9+6*25+5*23+6*18+7*20=796 д.е.

2. Находим цены свободных клеток:

Нашли клетку с отрицательной ценой ₂₁=-4, для которой будем строить цикл пересчета, т.к. отрицательная цена означает, что при перевозке одной единицы груза по данному циклу общая стоимость перевозок уменьшится на 4 единицы, а перевозится k-единиц груза.

3. Находим величину k, как минимум из отриц. вершин

k=min{22;25}=22

k* ₂₁=22*(-4)=-88

Это означает, что перевозка 22 единиц груза по данному циклу уменьшит общую стоимость перевозок на 88 д.е.

Z₁^ож=796-88=708 д.е.

При правильной переброске груза по данному циклу Z₁^ож должно совпасть с результатом первой проделанной итерации, что служит контролем хода вычислений.

Проделаем первую итерацию.

4. bj ai	22	34	41	20
   31	10	7 31	6	8
   48	5 22	6 3	5 23	4
   38	8	7	6 18	7 20

m+n-1=6

Z₁=7*31+5*22+6*3+5*23+6*18+7*20=708 д.е.

5. Циклически повторяем п.2, т.е. снова ищем свободную клетку с отрицательной ценой.

k=min{20;23}=20

k* ₂₄=20*(-2)=-40

Z₂^ож=708-40=668 д.е.

6. Проделаем вторую итерацию.

bj ai	22	34	41	20
31	10	7 31	6	8
48	5 22	6 3	5 3	4 20
38	8	7	6 38	7

m+n-1=6

Z₂=7*31+5*22+6*3+5*3+4*20+6*38=668 д.е.

7. Снова проверяем план на оптимальность, т.е. находим цены всех свободных клеток.

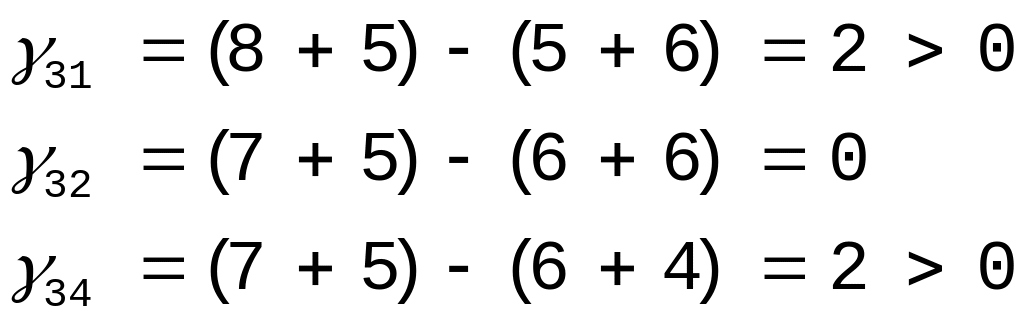
8. Для полного доказательства оптимальности плана пересчитывают цены всех оставшихся свободных клеток.

Свободных клеток с отрицательной ценой нет, значит план оптимальный и выписываем ответ.

9. Ответ:

x^*=

Z^*=668 д.е.

Замечание:

- при проверке цен свободных клеток, т.е. при доказательстве оптимальности плана мы получили две нулевые цены для клеток (1,3) и (3,2). Это означает, что оптимальный план не единственный и существует ещё два плана с той же общей стоимостью перевозок 668 д.е. При необходимости можно найти эти планы, пересчитав циклы с нулевой ценой.

- достоинством распределительного метода является простота и наглядность, и тот факт, что при доказательстве оптимальности плана видно, единственный он или нет.

- распределительный метод обладает одним, но существенным недостатком: для того, чтобы доказать оптимальность плана нужно отыскать циклы для всех свободных клеток и просчитать их цены. Если таких клеток много, то процесс становится трудоёмким.