Формулы Тейлора для важнейших элементарных функций
Если положить в этой формуле х=1, то
Таким образом, выбирая соответствующее число членов ряда n, можно вычислить число е с любой требуемой точностью.
2)
Если
nчетное
число, то
Остаток
для любого х
стремится к нулю при
.
2.11. Раскрытие неопределенностей. Правило Лопиталя
Теорема 1.
Пусть
функции f
и
непрерывны и имеют производные в
окрестности точки а
( а
– число или
),
за исключением, может быть, точки а,
при этом
не равны нулю в указанной окрестности
и
.
Тогда, если существует предел
(конечный
или бесконечный), то существует также
равный ему предел
В частности, здесь может идти речь о правом или левом пределе, и тогда под окрестностью точки а понимается правая или левая ее окрестность.
Доказательство (для случая а – конечного).
Полагая
доопределим
функции f(x)
и
так, чтобы они были непрерывны в точке
х=а.
Тогда функции f(x)
и
удовлетворяют условиям теоремы Коши и
для любой точки х
из рассматриваемой окрестности найдется
между а
и х
точка
такая,
что
Замечание 1.
Обратное утверждение неверно. Именно из существования предела
следует
наличие предела
,
но не наоборот!
Замечание 2.
Если
и производные
удовлетворяют тем условиям, которые
наложены на f
и
, то
Формула (1) называется правилом Лопиталя по имени французского математика, применившего ее для весьма простых случаев. Впрочем, до Лопиталя это правило было известно швейцарскому математику Бернулли.
Примеры использования правила Лопиталя:
В
последнем случае правило Лопиталя было
применено трижды, т.к. неопределенность
вида
получалась как для функций, так и для
первых и вторых производных.
Теорема 2.
Пусть
функции
непрерывны и имеют производные
в
окрестности (в частности, в левой или
правой окрестности) точки а
(конечной или бесконечной), за исключением
самой точки а.
При
этом
в указанной окрестности и
.
Тогда, если
существует предел
то существует равный ему предел
(без
доказательства).
Пример 1.
Легко доказать, что для любого натурального n
Пример 2.
Мы
рассмотрели примеры раскрытия
неопределенностей вида
или
.
Встречаются неопределенности вида:
Путем подходящих замен переменных они, как правило, сводятся к неопределенностям вида или .
Пример 3.
Пример 4.
2.12. Исследование функции одной переменной
2.12.1. Отыскание участков монотонности функции
Мы уже установили ряд условий, обеспечивающих возрастание, убывание, невозрастание и неубывание функции. Для удобства еще раз сформулируем эти условия:
1) Для того, чтобы дифференцируемая на интервале (a,b) функция f(x) возрастала, необходимо, чтобы ее производная всюду на интервале была строго положительна. Если же всюду отрицательна, то функция f(x) убывает на этом интервале.
2) Если функция f(x) дифференцируема на интервале (a,b) и ее производная неотрицательна, то функция не убывает на этом интервале. Если производная не положительна, то функция не возрастает.
Таким образом, вопрос об участках монотонности дифференцируемой функции f(x) сводится к исследованию знака первой производной этой функции.
Пример.
Отыскать участки монотонности функции
x
0
2
+
–
+
О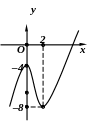
твет:
функция возрастает на интервалах
и убывает на интервале (0,2).
Ее график имеет вид.