1.3.7. Эквивалентные бесконечно малые функции и их

применение для вычисления пределов

Определение.

Бесконечно малые функции называются эквивалентными бесконечно малыми при , если

Пишут так: при .

Теорема.

Пусть в окрестности точки , за исключением, быть может, ее самой, задана функция и бесконечно малые функции . Тогда

Это равенство понимается в смысле: если существует предел его правой части, то существует равный ему предел левой части (и обратно). Отсюда же следует, что если один из пределов не существует, то не существует и другой.

Доказательство.

Пусть тогда

Аналогично доказывается обратное утверждение.

Пары эквивалентных бесконечно малых, которые используют при вычислении пределов:

9) при

1.3.8. Монотонные функции. Теорема о существовании

и непрерывности обратной функции

Определение.

Функция называется неубывающей (невозрастающей) на отрезке , если для любых

выполняется неравенство .

Неубывающие и невозрастающие функции называются монотонными.

Если неравенства строгие, то функция называется возрастающей (убывающей) на отрезке. Возрастающие и убывающие функции называются строго монотонными.

Теорема.

Рассмотрим непрерывную строго возрастающую функцию на отрезке , причем Тогда существует обратная к f функция , однозначная, строго возрастающая и непрерывная на .

Доказательство существования.

Поскольку каждому значению соответствует только одно значение , то любому значению y из можно поставить в соответствие именно то значение x, для которого обозначим это соответствие так: . Тем самым определена обратная функция.

Доказательство возрастания.

Из условия возрастания следует: если Верно и обратное утверждение: если

Но и получаем: если т.е. обратная функция – возрастающая.

Доказательство непрерывности обратной функции.

Докажем непрерывность обратной функции в произвольной точке . Обозначим и выберем произвольное , такое, что . Пусть

Выберем Тогда, очевидно,

а . (*)

Пусть теперь , т.е. .

С учетом (*) можно записать, что .

В силу возрастания функции следует, что

Но , поэтому или А это и означает, что функция непрерывна в точке

1.3.9. Разрывы первого и второго рода

Определение. Пусть функция определена на интервале (a, b), кроме, быть может, точки . Точка с называется точкой разрыва функции , если функция f не определена при , или если она определена в этой точке, но не является в ней непрерывной.

O

Рассмотрим график . Кружок в точке А означает, что эта точка входит в область значений , т.е. . Стрелка в точке В означает, что точка В в область значений функции не входит. Поскольку , функция имеет разрыв в точке с.

Другие возможные случаи разрывов.

c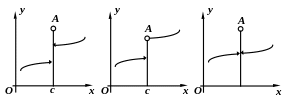

Если функция f имеет конечные пределы и , но , то функция имеет в точке разрыв I рода.

Если , то в точке устранимая особенность.

y

Если доопределить так, что , то получим непрерывную функцию.

Пример разрывной функции (функция Кронекера):

Точка является точкой разрыва I рода.

Если у функции не существует ни левого, ни правого предела, либо одного из них, либо эти пределы бесконечны в точке С, то функция имеет разрыв II рода.

Пример 1.

;

–точка разрыва II рода.

Пример 2.

Ее график имеет вид:

y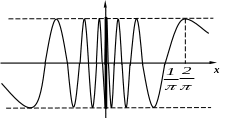

Эта функция не имеет в точке ни левого, ни правого предела. – точка разрыва II рода.

Пример 3.

Точки , – точки разрыва II рода. В них не определена, а пределы слева и справа бесконечны.

1.3.10. Функции, непрерывные на отрезке

Определение.

Функция называется непрерывной на отрезке , если она непрерывна во всех точках интервала , непрерывна справа в точке a, слева в точке b.

Теорема 1.

Если функция непрерывна на отрезке , то она ограничена на нем, т.е. существует число , такое, что для всех .

Теорема 2 (теорема Вейерштрасса).

Если функция непрерывна на отрезке , то она достигает минимума и максимума на , т.е. существуют точки , такие, что для всех .

Теорема 3.

Если функция непрерывна на и числа не равны нулю и имеют противоположные знаки, то на интервале имеется по крайней мере одна точка c, такая, что .

2.ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

2.1. Производная. Ее физический и геометрический

смысл

Пусть функция определена на интервале . Возьмем какое-либо значение и дадим аргументу x произвольное приращение , такое, что .

Назовем приращением функции величину .

Мы уже раньше выяснили, что если при , то функция непрерывна в точке х:

если , то функция непрерывна. Будем считать функцию непрерывной.

Будем также считать, что и составим отношение .

Т.к. величина аргумента x фиксирована, а произвольное приращение аргумента, то отношение представляет собой функцию от . Это отношение определено при небольших (в окрестности точки ) за исключением точки . Мы имеем право рассматривать вопрос о существовании предела этого отношения при .

Определение.

Производной функции в точке х называется предел (если он существует) отношения приращения функции к приращению аргумента, когда последний стремится к нулю.

Обозначение: .

Отметим, что если определена на и если при всех имеется производная, то эта производная является функцией и эта функция также определена на интервале .

Физический смысл производной

Пусть функция описывает закон движения точки по прямой линии, причем х представляет собой время, а у – путь, пройденный за это время точкой от начала отсчета пути. Тогда – средняя скорость движения за промежуток времени от х до , а – мгновенная скорость в момент времени х. В этом и заключается физический смысл производной (точнее говоря, механический).

Точно так же можно считать, что х – время, а функция определяет количество электричества, прошедшее через поперечное сечение некоторого проводника за время х. В этом случае определяет скорость изменения во времени количества электричества, т.е. представляет собой силу тока в проводнике в момент времени х.

Геометрический смысл производной

Р ассмотрим график функции на интервале . Пусть , а – произвольное приращение аргумента. Пусть М и Р – точки графика, соответствующие значениям аргумента х и .

Проведем , . Тогда Проведем секущую MP. Обозначим угол ее наклона к оси x .

Тогда, очевидно, . (*)

Теперь устремим к нулю. Очевидно, точка Р на графике будет приближаться к точке М, а секущая МР будет поворачиваться относительно точки М. При этом угол будет изменяться. Поскольку в равенстве (*) правая часть имеет предел при , равный значению производной , это означает, что существует предельное значение угла при . В этом случае говорят, что график имеет в точке x касательную, тангенс угла наклона этой касательной к оси Ох равен производной в точке х. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом этой прямой. Таким образом, геометрический смысл производной состоит в следующем: производная равна угловому коэффициенту касательной к графику функции в точке х.

Понятие правой и левой производной

Определение.

Правой(левой) производной функции в точке х называется .

Обозначается: правая, левая произ-водные.

Если функция имеет в точке х производную, то она имеет в этой точке и левую и правую производные, причем они совпадают. Если функция имеет в точке х и правую и левую производные, и они совпадают, то функция имеет в этой точке производную.

Пример функции, имеющей левую и правую производную, но не имеющей производной.

Пусть

Правая производная

Левая производная

Производной нет, т.к. нет касательной!

График:

Теорема о непрерывности функции, имеющей производ-

ную

Если функция f имеет производную в точке х, то она непрерывна в этой точке.

Доказательство.

Из существования предела при следует, что , где при . Отсюда

Перейдем к пределу при .

Это и означает непрерывность функции.

Обратное утверждение, вообще говоря, не верно.

Непрерывная функция может не иметь производной. Пример мы уже имели:

В точке х=0 функция непрерывна, но произ-водной не имеет.