
Свойства:
1) Если в систему столбцов входит нулевой столбец, то они ЛЗ.
2) Если в системе столбцов имеется два равных столбца,то она ЛЗ.
3) Если в системе столбцов имеется два пропорциональных столбца( Aj=лAj), то она ЛЗ.
4) Система из k>1 столбцов ЛЗ тогда и только тогда,когда хотя бы один из столбцов есть ЛК остальных.
5)Любые столбцы, входящие ЛНЗ систему, образуют ЛНЗ подсистему.
6) Система столбцов, содержащих ЛЗ подсистему, ЛЗ.
7) Если система столбцов А1…Аk – ЛНЗ, а после присоединения к ней столбца А – оказывается ЛЗ, то столбец А можно разложить по столбцам A1,...,Ak и притом единственным образом,т.е. с коэффициентом разложения находящимся однозначно.
Доказательство: 1A1+...+kAk+A=0 не все 1..k, =0 пусть =0 => 1A1+..+kAk=0, тогда все 1..k, = 0, противоречие. Ч.Т.Д.
10 -----------------------------------------
Базисный минор матрицы:
Пусть А- матрица m x n, k- натуральное число, не превосходящее m и n.
Минором k-го порядка матрицы А называется определитель матрицы k-го порядка, образованный элементами, стоящими на пересечении произвольно выбранных k строк и k столбцов матрицы А.
В матрице А размером m x n минор r-го порядка называется базисным,если он отличен от нуля,а все миноры (r+1)-го порядка равны нулю или их вообще не существует. Столбцы и строки, входящие в базичный минор ленейно независимы.
Теорема о базисном миноре: В произвольной матрице А каждый столбец(строка) является ЛК столбцов(строк),в которых расположен базисный минор.
Действительно, без ограничения общности предполагаем, что в матрице А размеров m x n базисный минор расположен в первых r строках и первых r столбцах.

Получим определитель,путем приписывания к базисному минору матрицы А соответствующих элементов s-й строки и k-го столбца. При 1=<s=<m , 1=<k=<n, D=0.
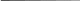
D=
Если s=<r или k<=r D содержит две одинаковые строки или два одинаковых столбца
Если s>r , k>r ;D=0, т.к является минором r+1-го порядка.
Раскладываем определитель по последней строке, получаем
as1* Dr+1 1 +… + asr * Dr+1 r +ask * Dr+1 r+1 =0, где Dr+1 j – алгебраическое дополнение элементов последней строки. Заметим,что Dr+1 r+1 не= 0, т.к. это базисный минор.
Поэтому ask= л1* as1+…+лr* asr, где
Лj= - (Dr+1 j/ Dr+1 r+1), j= 1,2,3…r/
Записываем последнее равенство для s=1,2,3…m, получаем
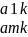 =
л1*
=
л1*
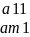 +…+
лr
*
+…+
лr
*
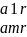
Т.е k-й столбец (при любом 1=<k=<n) есть ЛК столбцов базисного минора.
11 -----------------------------------------
Ранг матрицы – порядок базисного минора, 0Rgmin(m,n). (m,n-размерность матрицы).
(Если матрица нулевая, то и ранг, соответственно, =0). У матрицы может быть несколько базисных миноров.
Ранг матрицы равен наибольшему порядку отличного от нуля минора этой матрицы.
Если квадратная матрица невырожденная-ранг равен порядку, иначе меньше порядка.
Ранг блочной матрицы определяется как ранг обычной матрицы.При этом rg(A|B)>=rgA
Теорема о ранге матрицы: Ранг матрицы равен максимальному числу линейно независимых строк. Доказательсто: 1)Пусть rgA=r. Тогда в матрице А имеется r ЛНЗ строк. Строки в которых расположен базисный минор. Если бы они были ЛЗ, то этот минор был бы равен нулю, а ранг матрицы А не равнялся бы r.
2)Покажем,что r – максимальное число ЛНЗ строк,т.е. любые p строк матрицы ЛЗ при (p>r). Из них составим матрицу B. Поскольку матрица В-часть матрицы А, то rgB=<rgA. => Есть строка матрицы В, не принадлежащая базисному минору, тогда, по теореме о базисном миноре она равна ЛК строк, в которых расположен базисный минор=> строки матрицы В ЛЗ. Таким образом, в матрице А не более, чем r ЛНЗ строк.
Следствие:
Максимальное число ЛНЗ строк в матрице равно максимальному числу ЛНЗ столбцов
rgA=rgAT
При элементарных преобразованиях строк матрицы ЛЗ или ЛНЗ любой системы столбцов этой матрицы сохраняется.
12 -----------------------------------------
Теорема о ранге произведения матриц:
C=AB, тогда RgC Rg A. RgC Rg B. Любой столбец C – линейная комбинация столбцов A. Rg C Rg (A|B).
Доказательствоя: rg(A*B)=rg(A)*rg(B), причем A(mxp), B(pxn);C(mxn)=AB, тогда RgC<= RgA. Любой столбец C – линейная комбинация столбцов A. Rg C <= Rg (A|С). Аналогично для B. ч.т.д.
13 ------------------------------------------
Необходимое и достаточное условие равенства нулю определителя:
Определитель квадратной матрицы равен нулю тогда, когда один ее столбец
равен линейной комбинации остальных. (Det A=0; Anxn, rg A<n)
Именно он является линейной комбинацией базисного минора, => и столбцов
Матрицы. Если какая-либо строка является линейной комбинацией остальных,
то ее можно вычеркнуть, при этом ранг не изменится.
14 -----------------------------------------
Алгоритмы нахождения ранга матрицы:
Метод окаймляющих миноров: Находим M11(минор первого порядка).Если M110, то rgA>1. Находим минор второго порядка. Если 0, rgA>=2. Находим минор r-го порядка. Если 0, тогда rgA > r. Если нет миноров, => rgA=r(r линейно-независимых столбцов).
Метод Гаусса: Элементарными преобразованиями приводим матрицу к ступенчатому виду. Количество ненулевых строк и будет рангом матрицы.
15 -----------------------------------------
Cистемой
m
линейных алгебраических уравнений с n
неизвестными называется система
уравнений вида
Числа aij ,i=1,..,m ; j=1,...,n называются коэффициентами системы.
b1,b2,…bn-свободные члены
x1,x2,…xn-неизвестные
Решение системы – упорядоченная совокупность n чисел (α1, α2,… αn) такая, что после замены неизвестных x1,x2,…xn соответствубщими числами α1, α2,… αn каждое уравнение превращается в верное числовое равенство.
Система совместна- хотя бы одно решение
Система несовместна- нет решений
Система однородная- свободные члены равны нулю
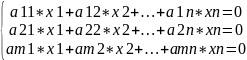
А=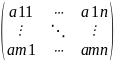 – матрица системы
– матрица системы
b=
( столбец свободных членов
столбец свободных членов
х=
( столбец
неизвестных
столбец
неизвестных
Матричная запись системы уравнений имеет вид Ах=b, у однородной Ах=0
