Векторное произведение:

Векторным произведением векторов a и b называется число равное произведению длин этих векторов на синус угла между ними.

Вектор с называется векторным произведением неколлинеарных векторов a и b,если:

1)его длина равна произведению длин векторов а и b на синус угла между ними

2)вектор с ортогонален векторам а и b

3)векторы a,b,c( в указанном порядке)образуют правую тройку.

Свойства:

1)[a,b]=-[b,a] антисимметричность

2)[a+b,c]=[a,c]+[b,c]аддитивность,

однородность

3)[ *a,b]= *[a,b] аддитивность,однородность

c=[a;b]=|a||b|sinA=(матрица 3x3: i, j, k, x1, x2, x3, y1, y2, y3).

S_#a,b=|[a, b]|

S_{треугольника}= (S_#a,b)/2

h=|[a;b]|/SQRT(a;a)

Если a||b, то [a;b]=0

26 -----------------------------------------

Смешанное произведение:

Смешанным произведением векторов а,b,c называется число (а,[b,c]),равное скалярному произведению вектора а на векторное произведение векторов b и с.

Геометрические свойства:

1)Смешанное произведение – число равное объему параллелепипеда, построенного на векторах a, b, c, взятого со знаком “+”, если векторы образуют правую тройку.

2)Смешанное произведение (a,b,c) равно нулю тогда и только тогда,когда векторы a,b,c компланарны.

Алгебраические свойства:

1)При перестановке двузх множителей смешанное произведение меняет свой знак на противоположный,а при циклической перестановке – не изменится

2) Смешанное произведение линейно по любому сомножителю:

(a + b; c; d) = (a + b; [c; d])= (a; [c; d])+(b; [c; d]).

=(a; c; d)+(b; c; d).

(a;b;c)=(a; [b;c]) = (матрица 3x3: x₁, x₂, x₃; y₁, y₂, y₃; z₁, z₂, z₃)

h=|(a;b;c)|/|[a;b]|

Если (a;b;c)>0, то это правая тройка.

Если (a;b;c)<0, то это левая тройка.

Если (a;b;c)=0, то a,b,c – компланарны.

V_{a, b, c}= |(a;b;c)|

27 -----------------------------------------

1)Вектор а=0 тогда и только тогда,когда

(а,а)=0  x²+y²+z²=0  x=y=z=0

2)Ненулевые векторы а и b ортогональны тогда и только тогда,когда

(a,b)=0  xa*xb+ya*yb+za*zb=0

3)Векторы a и b коллинеарны тогда и только тогда,когда

[a;b]=0  матрица 3x3: i, j, k, x1, x2, x3, y1, y2, y3) =0  xa/xb=ya/yb=za/zb

4)Векторы a,b,c компланарны тогда и только тогда,когда

(a;b;c)=0  (матрица 3x3: x₁, x₂, x₃; y₁, y₂, y₃; z₁, z₂, z₃)=0

5)Длина вектора а вычисляется по формуле

|a|=SQRT(a,a)=SQRT(x²+y²+z²)

6)Угол fi между ненулевыми векторами a и b вычисляется по формуле:

Сos(fi)=(a,b)/(sqrt(a,a)*sqrt(a,b))= (x_ax_b+y_ay_b+z_az_b)/sqrt(x_a^2+y_a^2+z_a^2)*sqrt(x_b ^2+y_b^2+z_b^2)

7)Алгебраическое значение длины ортогональной проекции вектора а на ось, задаваемую вектором b не=0, находится по формуле:

Пр_ba=(a,b)/|b=(x_ax_b+y_ay_b+z_az_b)/sqrt(x_b^2+y_b^2+z_b^2)

8)Ортогональная проекция вектора а на ось, задаваемую вектором b не=0 :

Пр_ba=((a,b)/(b,b))*b=(x_ax_b+y_ay_b+z_az_b/x_b^2+y_b^2+z_b^2)*(x_b*i+y_b*j+z_b*k)

9)Направляющие косинусы вектора а находятся по формулам:

Cosα=(a,i)/|a|=x_a/(x_a^2+y_a^2+z_a^2)

Cosα=(a,j)/|a|=y_a/(x_a^2+y_a^2+z_a^2)

Cosα=(a,k)/|a|=z_a/(x_a^2+y_a^2+z_a^2)

10)Единичный вектор е,одинаково направленный с вектором а,находится по формуле:

e= a/|a|=i*cosα+ j*cosβ+ k*cosµ

11)Площадь параллелограмма S_#a,b=|[a, b]|

12)Объем параллелепипеда V_{a, b, c}= |(a;b;c)|

13)Тройка некомпланарных векторов a,b,c

Если (a;b;c)>0, то это правая тройка.

Если (a;b;c)<0, то это левая тройка.

14)Высота h параллелограмма h=|[a;b]|/SQRT(a;a)

15)Высота h параллелепипеда h=V_a,b,c/ S_#b,c=|(a;b;c)|/ |[b, c]|

16)Угол ψ между вектором а и плоскостью,содержащей векторы b и с.

sin ψ=|cosu|=|(a;b;c)|/|a|* |[b, c]|

17)Угол ϭ между плоскостями,содержащими векторы a,b и c,d соответственно

cos ϭ = |([a,b],[c,d])|/ |[a,b]|*|[c,d]|

28 -----------------------------------------

Понятие об уравнении линии и поверхности:

Пусть задана система координат. Под уравнением множества M, в этой системе координат, понимается равенство, связывающее координаты точек. например:

а) (x-x₀)²+(y-y₀)²=R² – окружность.

б) (x-x₀)²+(y-y₀)²+(z-z₀)²=R² – сфера.

в) |y|=<1, xIR - прямая.

Уравнение ---:

P(x)=a₁x^k1 + … + a_nx^kn, где k – целое неотр., max(k_n)=степень.

Уравнение линии:

P(x, y) =a₁x^k1y^L1 + … + a_nx^kny^Ln, где k, L – целое неотр., max(k_n + L_n)=степень.

Уравнение поверхности:

P(x, y, z) =a₁x^k1y^L1z^M1 + … + a_nx^kny^Lnz^Mn, где k, L, m – целое неотр., max(k_n + L_n+ m_n)=степень.

Алгебраические линии и поверхности:

Алгебраической линией(поверхностью) называется множество точек на плоскости(в пространстве), которое к какой-либо системе координат может быть задано уравнением вида P(x;y)=0 (P(x;y;z)=0), где P – многочлен.

Порядком линии называется степень данного многочлена.

Пример:

P(x;y;z)=x2+y2+z2-1=0 – алгебраическая поверхность.

y – sin(x)=0 – не алгебраическая поверхность, т.к. не может быть задана уравнением P.

Теорема об инвариантности порядка алгебраической поверхности(линии):

Пусть уравнение имеет вид P(x;y)=0, тогда в любой другой аффинной системе координат это уравнение будет иметь уравнение того же вида и того же порядка.

29 -----------------------------------------

Прямая на плоскости:

Ненулевой вектор перпендикулярный прямой(плоскости) называется нормальным(нормаль обозначается n) по отношению к этой прямой(плоскости).

M₀M перпендикулярно n;

((M₀M), n) = 0

(r-r₀, n)=0 – уравнение прямой. => (r, n)+C=0, где C=(r₀, n);

Ax + By + C=0 – общее уравнение прямой.

Любая прямая на плоскости может мыть задана этим уравнением.

Если A = 0 , то уравнение не содержит x и представляет собой прямую, параллельную оси Ox.

Если B = 0 , то уравнение не содержит y и представляет собой прямую, параллельную оси Oy и преобразуется к виду:

y=kx+b, где k(k=-A/B) - тангенс угла наклона, а b(b=-C/B) – начальная ордината.

Нормальное уравнение прямой:

cos(a)=A/+-sqrt(A²+B²)

cos(b)=B/+-sqrt(A²+B²)

xcos(a)+ycos(b)-p=0

Каноническое уравнение прямой:

(x-x0)/a=(y-y0)/b

Уравнение прямой,проходящей через 2 заданные точки:

x-x0/x1-x0=y-y0/y1-y0

Уравнение прямой в отрезках

x/x1+y/y1=1

Параметрическое уравнение

x=x0+a*t

y=y0+b*t , t прин R

Угол между двумя прямыми:

Угол между их направляющими векторами

Если прямые заданы:

y=k₁x+b₁

y=k₂x+b₂, то угол между ними равен: tg()=(k₁-k₂)/(1+k₁k₂).

Если прямые заданы:

A₁x + B₁y + C₁=0

A₂x + B₂y + C₂=0, то угол между ними равен: tg()=(A₁B₂-A₂B₁)/(A₁A₂+B₁B₂).

Cos(u)=(p1,p2)/|p1|*|p2|=(a1*a2+b1*b2)/(sqrt(a1^2+b1^2)* sqrt(a2^2+b2^2))

Расстояние от точки до прямой:

M₁(x₁;y₁) и Ax + By + C=0, то h = |(Ax₁ + By₁ + C)|/SQRT(A²+B²);

h=(S_#P,MoM)/|P|

30 -----------------------------------------

Плоскость и уравнения ее задания:

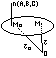
((M₀M), n) = 0

(r-r₀, n)=0 – уравнение плоскости. => (r, n)+D=0, где D=(r₀, n);

Ax + By + Cz + D =0 – общее уравнение плоскости.

Любая плоскость в пространстве может мыть задана этим уравнением.

Параметрическое уравнение

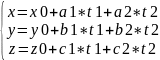,t1,t2 принадлеж R

Плоскость, проходящая через две точки M₀(x₀;y₀;z₀), M₁(x₁;y₁;z₁) и перпендикулярная плоскости, заданной уравнением Ax+By+Cz+D=0:

| x-x₀ y-y₀ z-z₀ |

|x₁-x₀ y₁-y₀ z₁-z₀|=0

| A B C |

Плоскость, проходящая через точку M₀(x₀;y₀;z₀) и перпендикулярная двум плоскостям, заданным уравнениями Ax₁+By₁+Cz₁+D₁=0 и Ax₂+By₂+Cz₂+D₂=0:

| x-x₀ y-y₀ z-z₀ |

| a₁ b₁ c₁ |=0

| a₂ b₂ c₂ |

xcos()+ycos()+zcos()-p=0 - нормальное уравнение плоскости.

x/a+y/b+z/c=1 - уравнение плоскости в отрезках.

Расстояние от точки до плоскости:

Если M₁(x₁;y₁;z₁) и Ax + By + Cz + D = 0, тогда

h=(|Ax₁ + By₁ + Cz₁ + D|)/SQRT(A² + B² + C²);

Угол между двумя плоскостями:

A₁x + B₁y + C₁z +D₁ = 0 и

A₂x + B₂y + C₂z +D₂ = 0, тогда

cos()= (A₁A₂+B₁B₂+C₁C₂)/(SQRT(A₁²+B₁²+C₁²) SQRT(A₂²+B₂²+C₂²));

31 -----------------------------------------

Прямая линия в пространстве и виды ее записи.

- общее уравнение прямой в пространстве, задаваемой двумя пересекающимися плоскостями:

П₁ не параллельно П₂.

Параметрический вид:

x=x₀ + at,

y=y₀ + bt,

z=z₀ + ct, tR.

Канонический вид:

(x-x₀)/a=(y-y₀)/b=(z-z₀)/c

Если a=0, то x=x_0, (y-y₀)/b=(z-z₀)/c

Если a=b=0, то x=x_0, y=y_0, z=z₀

Запись через координаты двух точек:

P=M₀M (x-x₀)/(x₁-x₀)= (y-y₀)/(y₁-y₀)= (z-z₀)/(z₁-z₀)

Угол между двумя прямыми:

Если прямые заданы:

y=k₁x+b₁

y=k₂x+b₂, то угол между ними равен: tg()=(k₁-k₂)/(1+k₁k₂).

Если прямые заданы:

A₁x + B₁y + C₁=0

A₂x + B₂y + C₂=0, то угол между ними равен: tg()=(A₁B₂-A₂B₁)/ (A₁A₂+B₁B₂).

Cos(u)=|(p1,p2)|/|p1|*|p2|=|a1*a2+b1*b2+c1*c2|/sqrt(a1^2+b1^2+c1^2)* sqrt(a2^2+b2^2+c2^2)

Расстояние от точки до прямой:

M₁(x₁;y₁,z1) и l: (x-x₀)/a=(y-y₀)/b=(z-z₀)/c

, то d =|[m,p]|/|p|=

Sqrt(( )^2+( )^2+ )^2)/sqrt(a^2+b^2+c^2)

p=a*i+b*j+c*k

m=M0M1=(x1-x0)*i+(y1-y0)*j+(z1-z0)*k

Расстояние между скрещивающимися прямыми:

d =|(m,p1,p2)|/|[p1,p2]|

m=M1M2=(x2-x1)*i+(y2-y1)*j+(z2-z1)*k

p1=a1*i+b1*j+c1*k

p2=a2*i+b2*j+c2*k

| x2-x₁ y1-y₂ z1-z₂ |

| a₁ b₁ c₁ |=(m,p1,p2)

| a₂ b₂ c₂ |

Угол между прямой и плоскостью:

Ax + By + Cz +D=0

sin(a)=|(n,p)|/|n||p|=|a*A+b*B+c*C|/sqrt(a^2+b^2+c^2)*sqrt(A^2+B^2+C^2)

32 -----------------------------------------

Условие параллельности и совпадения прямых:

Если прямые заданы:

y=k₁x+b₁

y=k₂x+b₂, то они параллельны, если k₁=k₂;

Если же: k₁=k₂ и b₁=b₂, то они совпадают.

Если же k₁*k₂=-1, то они перпендикулярны.

Две прямые называются коллинеарными,если они параллельны или совпадают.

Если прямые заданы:

A₁x + B₁y + C₁=0

A₂x + B₂y + C₂=0, то они параллельны, если A₁B₂=A₂B₂=0;

Если же: A₁/A₂=B₁/B₂=C₁/C₂, то они совпадают.

Прямые параллельны или совпадают,если существует такое число л не=0,что

n1=л*n2 

Если же A₁A₂+B₁B₂=0, то они перпендикулярны.

Условие параллельности и совпадения двух плоскостей:

A₁x + B₁y + C₁z +D₁ = 0, n₁=(A₁, B₁, C₁);

A₂x + B₂y + C₂z +D₂ = 0, n₂=(A₂, B₂, C₂);

A₁/A₂=B₁/B₂=C₁/C₂не=D1/D2- плоскости параллельны, т.е. n₁ и n₂ коллинеарны.

A₁/A₂=B₁/B₂=C₁/C₂=D₁/D₂- плоскости совпадают.

Плоскости параллельны или совпадают,если существует такое число л не=0,что

n1=л*n2 

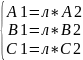
Прямые в пространстве

-прямые скрещиваются, т.е не лежат в одной плоскости:

-прямые пересекаются, лежат в одной плоскости и имеют одну общую точку

-прямые параллельны, лежат в одной плоскости и не пересекаются

-прямые совпадают.

33.----------------------------------------

Oe1e2 - “старый базис”; Oe1’e2’ – “новый базис”

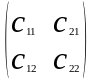
Поворот – осуществляется с помощью матрицы перехода (квадратная матрица второго порядка). 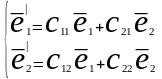где с₁₁ и с₂₂ это cos , с₂₁ – sin , а с₁₂ - -sin 

При параллельном переносе из координат точки вычитают координаты нового базиса в старом, матрица перехода не нужна, так как она единичная.

При изменении названий надо применить матрицу перехода .

При изменении направления оси координат (прим Х) надо применить матрицу перехода .

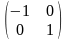34. ----------------------------------------

(*) Ax₂+Bxy+Cy²+Dx+Ey+F=0 – формула линии второго порядка.

x²/a²-y²/b²=0 – каноническое ур-ние двух пересекающихся прямых.

F<>0 то x²/a²-y²/b²=1 – каноническое ур-ние гиперболы.

Если A*C>0 то

AF>0 то x²/a²+y²/b² = -1 – каноническое уравнение мнимого эллипса.

AF<0 то x²/a²+y²/b² = 1 – каноническое уравнение эллипса.

F=0 то x²/a²+y²/b² = 0 – каноническое уравнение двух мнимых пересек. прямых.

Если C<>0 то

D<>0 то y²=2px каноническое уравнение параболы.

D=0 т.е. Cy²+F=0

CF>0 т.е. y²+a²=0 – каноническое уравнение двух мнимых параллельных прямых.

CF<0 т.е. y²-a²=0 - каноническое уравнение двух параллельных прямых.

F=0 т.е. y²=0 пара совпадающих прямых.

35. ----------------------------------------

Эллипс – геометрическое место точек плоскости, расстояние от каждой до двух заданных (F1, F2) есть, постоянная величена (2А). 2С – фокусное расстояние равное F1F2.

Малая полу ось В=|A²-C²|^0.5. Большая полуось – А.

Эксцентриситет – величина равная отношению половины фокусного расстояния к половине заданной величины, у эллипса всегда от 0 до 1, у гиперболы больше 1.

Гипербола – геометрическое место точек на плоскости, модуль разности расстояний от каждой до двух заданных (F1 и F2) есть постоянное число (2А).

Парабола - геометрическое место точек на плоскости, равно удаленных от данной точки (фокуса) и прямой (директриса).

36.

1. уравнение эллипсоида;

2. уравнение мнимого эллипсоида;

3. уравнение мнимого конуса;

4. уравнение однополостного гиперболоида;

5. уравнение двуполостного гиперболоида;

6. уравнение конуса;

7. уравнение эллиптического параболоида;

8. уравнение гиперболического параболоида;

9. уравнение эллиптического цилиндра;

10. уравнение мнимого эллиптического цилиндра;

11. уравнение пары мнимых пересекающихся плоскостей;

12. уравнение гиперболического цилиндра;

13. уравнение пары пересекающихся плоскостей;

14. уравнение параболического цилиндра;

15. уравнение пары параллельных плоскостей;

16. уравнение мнимых пары параллельных плоскостей;

17. уравнение пары совпадающих плоскостей.

37. ----------------------------------------

Координатное пространство Rⁿ – множество упорядоченных наборов из n действительных чисел.

Всякий вектор может быть разложен по базису, причём единственным образом.

Rⁿ e₁=(e₁₁,e₂₁,…,e_n1),…e_n=(e_1n,e_2n,…,e_nn); x=(x₁,x₂,…,x_n);

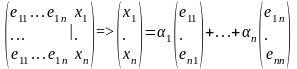
Док-во единственности: x=₁e₁+…+_ne_n; x=₁e₁+…+_ne_n => 0=(₁-₁)e₁+…+(_n-_n)e_n , т.к. e₁,…e_n – линейно не зависимы, то ₁=₁ и т.д.

Линейных операций над столбцами НЕТ!!!

38. ----------------------------------------

e^|=e*C где C матрица перехода. Матрица перехода от базиса e к базису e^| называется матрица, в i столбце которой находятся координаты нового базис вектора e^|_i в старом.

39. ----------------------------------------

Пусть дана квадратная матрица А размером MxN и не нулевой столбец Х, он называется собственным вектором этой матрицы, если выполняется равенство АХ=ЕХ. Число  называется собственным значением этой матрицы. (А-Е)Х=0, det(А-Е)Х=0 –характеристическое ур-ние.

Алгоритм нахождения собственного значения матрицы

1. Составить характеристическое уравнение det(А-Е)Х=0

2. Решить его и получить несколько 

3. Для всех собственных значений надо решить уравнение (А-₁Е)Х=0 Фундаментальная Система Решений – это все линейно не зависимые векторы принадлежащие собственным значениям ₁.

   

4. Для собственных значений ₂ и т.д.

А = 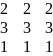А-Е=

1=..

2=…

1) 

Х= а( ) + b( )

Совокупность собственных значений – спектр матрицы. Если все n собственных значений матрицы различны, то говорят, что матрица имеет простой спектр.

40. ----------------------------------------

Две квадратные матрицы A и B называются подобными, если существует не вырожденная матрица C такая, что B=C^-1AC. A~A т.е. A=E^-1AE. A~B то B~A т.е. B=C^-1AC, A=CBC^-1, A=D^-1BD (меняем C на D^-1). A~B и B~D то A~D т.е. B=C^-1AC, D=F^-1BF, D=F^-1C^-1ACF, D=G^-1AG (меняем F^-1C^-1 на G^-1).

Для того чтобы привести матрицу к диагональному виду при помощи преобразования подобие необходимо и достаточно, чтобы она имела n линейно независимых собственных векторов.

(1) =C^-1AC (2) AC=C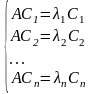 (1)~(2)

Необходимость: из =C^-1AC ( - диагональная) следует (2) след. C₁,C₂,…,C_n – Свободные векторы; Ax=x линейно не зависимые принадлежащие C^-1.

Достаточность: n линейно не зависимых свободных векторов, C₁,C₂,…,C_n (2) С=( C₁,C₂,…,C_n), C^-1 существует значит (1). Ч.Т.Д.

41. ----------------------------------------

Характеристические многочлены подобных матриц совпадают P_A=|A-E|; P_B=|B-E|=|C^-1 AC-C^-1EC|=|C^-1(A-E)C|=|C^-1|P_A|C|=P_A (B=C^-1AC).

Собственные значения подобных матриц совпадают.

Характеристический многочлен матрицы имеет вид: P_A=(-1)ⁿⁿ+(-1)^n-1S_pA^n-1+(-1)^n-2^n-2 *{сумму главных миноров второго порядка}+…+(-1) *{сумму главных миноров n-1 порядка}+det(A). Главные миноры порядка m – это миноры порядка m с одинаковыми номерами строк и столбцов.

Подобные матрицы имеют: равные определители, равные следы, равные суммы миноров 2-го порядка и т.д.

Собственные векторы при равных собственных значениях линейно не зависимы.

Определитель матрицы равен произведению её собственных значений. Det(A)= ₁₂…_n; P_A()=|A-E|=det(A); P_A()=(-1)ⁿ(-₁)…(-_n)=(-1)²ⁿ₁₂…_n =₁₂…_n (при =0).

Если спектр матрицы простой, то она приводиться к диагональному виду при помощи преобразования подобие. Раз спектр матрицы простой, то всё собственные значения различны, то у матрицы есть n различных собственных векторов.

Линейная комбинация собственных векторов, принадлежащих одному собственному значению, является собственным вектором, если он не нулевой.

42. ----------------------------------------

Не пустое подмножество Rⁿ называется линейным подпространством, если оно с любыми двумя векторами содержит их линейную комбинацию. Подпространство L имеет размерность K, если есть K линейно не зависимых векторов и K+1 линейно зависимых.

Множество решений однородной системы уравнений является подпространством Rⁿ и наоборот. Нет Док-ва.

43. ----------------------------------------

Не пустое подмножество Rⁿ называется аффинным подпространством, если с любыми двумя элементами оно содержит все их аффинные комбинации. Любая аффинная оболочка является плоскостью. Подпространство L имеет размерность K, если есть K линейно не зависимых векторов и K+1 линейно зависимых. Множество решений однородной системы уравнений, является аффинным подпространством (линейным многообразием) в Rⁿ.

Необходимость: x=xⁿ+c₁₁+…+c_n-2_n-2; x=xⁿ+e, eLin(ФСР).

Достаточность: П => x₀П: П=x₀+C (П - плоскость), L подпространство Rⁿ, e₁,…,e_k – Базис в L. Дополним его до базиса всего пространства: e₁,…,e_k,e_k+1,…,e_n – базис в Rⁿ. xП => x-xⁿL; x-xⁿ=₁l₁+…+klk+0lk₊₁+…+0l_n; (x-xⁿ)=C(x-xⁿ); (e старый)(e новый) (xⁿ – X новый) 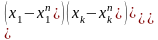(в новом базисе…в старом базисе); 0=A(x-xⁿ); b=Axⁿ; Ax=b.

Гиперплоскостью в Rⁿ называют множество решений уравнения a₁x₁+…+a_nx_n=b.

Любая плоскость может быть задана пересечением гиперплоскостей.

45. ----------------------------------------

Если P₀,…,P_r – геометрически не зависимые векторы в r мерной плоскости П, то любая точка P может быть представлена виде: ₀ P₀+..+_r P_r, где сумма всех  равна 1 и все  определены единственным образом.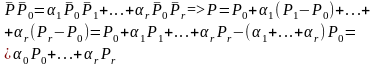

₀=1-₁-…-_r Коэффициенты  называют барицентрическими координатами т. P.

Механический смысл: Если в точках P₀,…, P_r разместить массы ₀,…, _r, то точка P будет центром масс. Если P₀,…, P_r – ГНЗ, то их выпуклая комбинация называется r мерным симплексом.