Аффинная система координат:

Аффинная система координат на плоскости задается точкой О (начало координат) и парой приложенных к ней неколлинеарных векторов e₁ и e₂, данных в определенном порядке. 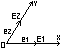Аффинная система координат необязательно прямоугольна.

Первая ось называется осью абсцисс(OX), а вторая ординат(OY). Сама система координат обозначается через Oe₁e₂ или Oxy.

Проекции векторов OM_x и OM_y называются соответственно первой и второй координатами точки M=(x;y).

Аффинная система координат в пространстве строится приблизительно так же как и на плоскости, только в данном случаи базис состоит из трех некомпланарных векторов e₁, e₂, e₃(ось Оz называется осью аппликат). Каждые две оси координат задают проходящую через них координатную плоскость. Каждая упорядоченная тройка чисел x, y, z однозначно определяет точку M.

22 -----------------------------------------

Выражение линейных операций над векторами через их координаты:

Сложение векторов: a₁ = (x₁, y₁, z₁); a₂ = (x₂, y₂, z₂); a=a₁+a₂=(x₁+x₂, y₁+y₂, z₁+z₂)

вычитание аналогично.

Умножение вектора на число: m₂=m₁, то m₂ = (x₁;y₁;z₁);

деление аналогично.

Деление отрезка в заданном отношении:

Если отношение AC к CB представить в нормированном виде, т.е. +=1, то OC = OB + OA.

23 -----------------------------------------

Прямоугольная система координат.

Ортом называется вектор длинна которого равна 1.

Аффинная система координат называется прямоугольной, если базис нормирован, т.е. |i|=|j|=|k|=1 и эти орты взаимно перпендикулярны.

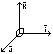
Вектор идущий от точки О – начала базиса к выбранную вами точке М называется радиус вектором к этой точке М и обозначается буквой r.

Прямоугольными координатами вектора m называются алгебраические проекции данного вектора на оси координат. m(x;y;z) или m = (x;y;z);

Выражение длин сторон вектора через его координаты:

Каждый вектор равен сумме его компонент по трем осям координат:

m=Пр_oxm + Пр_oym + Пр_ozm

Длинна вектора(|AB|) равна: |AB|=SQRT((x_a-x_b)²+(y_a-y_b)²+(z_a-z_b)²);

24 -----------------------------------------

Скалярное произведение:

Скалярным произведением двух ненулевых векторов a и b называется число равное произведению длин этих векторов на косинус угла между ними. Если косинус угла равен нулю, то и скалярное произведение равно нулю. Если хотя бы один из двух векторов нулевой, то угол между ними не определен,а скалярное произведение считается равным нулю.

(a, b)=|a||b|cosA=(x₁x₂+y₁y₂+z₁z₂)

Скалярное произведение ненулевых векторов а и b и равна произведению длины вектора b на алгебраическое значение длины ортогональной проекции вектора а на ось, задаваемую вектором b.

(a,b)=пр_ba|b|

Пр_ab=(a,b)/|a|

пр_ea=|a|cosA=(a;e)

a=(x, y, z); x=пр_ia=(a;i); y=пр_ja=(a;j); z=пр_ka=(a;k);

e=a/|a|=(cosA, cosB, cosY)

|a|=SQRT(a,a)=SQRT(x²+y²+z²)

Свойства:

1.(a,b)=(b,a) симметричность

2.(a+b,c)=(a,c)+(b,c) аддитивность,однородность

3.(*a,b)= *(a,b) аддитивность, однородность

4.(a,a)>=0, причем из равества (а,а)=0 => а=0 неотрицательность скалярного квадрата

(a;a)=|a|²

(a;b)=0, если вектор a перпендикулярен вектору b.

Замечание: скалярное произведение нельзя распространить на случай трех сомножителей.

Формула вычисления координат в ортонормированном базисе В ортонормированном базисе скалярное произведение векторов равно сумме произведений одноименных координат векторов:

Если векторы а и b относительно ортонормированного базиса плоскости имеют координаты xa,ya и xb, yb соответственно,то скалярное произведение этих векторов вычисляется по формуле (а,b)=xa*xb+ya*yb

Если векторы а и b относительно ортонормированного базиса плоскости имеют координаты xa,ya,za и xb,yb,zb соответственно,то скалярное произведение этих векторов вычисляется по формуле (а,b)=xa*xb+ya*yb+za*zb

25 -----------------------------------------