
======= ТЕМА 1 ========
1. Матрицы, виды матриц, операции над ними и их свойства:
Матрица mxn – прямокугольная таблица чисел, состоящая из m строк и n столбцов.
Виды:
Квадратная, где m=n(m – порядок матрицы).
Диагональные:
a) Просто диагональная - все элементы, кроме диагональных, = 0
b) Еденичная - диагональная, но все диагональные элементы = 1
c) Нулевая - все элементы = 0
d) Верхняя треугольная - все элементы над диагональю = 0
e) Нижняя треугольная - все элементы под диагональю = 0
f) Блочная.
Операции над матрицами:
1) A=B равенство (присваивание), одинаковые элементы
2) Сложение: C=A+B. cij=aij+bij. (i=1..m, j=1..n);
3) Умножение на число z0: B=z*A, bij=aij*z;
4) Умножение: C=A*B. [Amxp*Bpxn = Cmxn]. cij=aip*bpj, где p=MIN[m(A), n(B)];
5) Транспонирование: Amxn=Bnxm =AT (Bji=Aij);
Свойства: (A+B)T= AT+BT; (AB)T=BT*AT; (AT)T=A;
Свойства:
1) Ассоциативность [A(BC)=(AB)C];
2) Дистрибутивность [A(B+C)=AB+AC];
3) z(AB)=(zA)B;
4) ABBA;
2 ------------------------------------------
Блочные матрицы:
Если матрицу при помощи горизонтальных и вертикальных линий разбить на несколько частей, то эти части будут блоками, а матрица, составленная из этих блоков будет называться блочной матрицей(||A||). Элементы блочной матрицы, тоже матрицы, записываются при помощи больших букв с индексами, которые им даются по тем же правилам, что и индексы простых элементов.
Теорема о произведении блочных матриц:
Cik=Ai1B1k+…, где Ai1 и B1k блоки матриц A и B. Доказываеться перемножением.
Теорема:
Прямая сумма блочных квадратных матриц A и B: C=AB и C=||матрица 2x2: A,0;0,B||;
(AmAn)+(BmBn)=(Am+Bm)(An+Bn);
(AmAn)(BmBn)=AmBmAnBn;
3 ------------------------------------------
Индуктивное определение det A. Миноры и алгебраические дополнения.
1) Det A – это число,которое ставится в соответствие матрице А и вычисляется по ее элементам согласно следующим правилам.
1. Определителем матрицы А= (а11) порядка n=1 называется единственный элемент этой матрицы det( a11)=a11
2.
Определителем матрицы А порядка n>1
называется число detA=(-1)1+1
*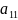 *
*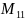 +(-1)
1+2*
+(-1)
1+2*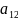 *
*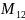 +…+(-1)
1+n*
+…+(-1)
1+n*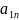 *
*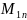
где Мij – дополнитльный минор элемента аij-определитель матрицы порядка n-1, полученной из матрицы А вычеркиванием i-й строки и j-ого столбца.
Алгебраическим дополнением Аij элемента aij матрицы А называется дополнительный минор Мij этого элемента, умноженный на (-1) i+j
Индуктивное определение позволяет вычислять определить любого порядка.
Матрица вырожденная,если ее определитель равен нулю, иначе- невырожденная.
Теорема о разложении определителя по элементам строки, столбца:
Определитель матрицы А равен сумме произведений элементов произвольной строки(столбца) на их алгебраическое дополнение.
detA=
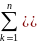 – разложение по i-ой
строке
– разложение по i-ой
строке
detA= – разложение по j-му столбцу
4 ------------------------------------------
Свойства определителей:
1) det AT = det A. Это означает равномерность строк и столбцов.
2) Если в определителе поменять местами 2 строки(столбца), то он поменяет знак.
3) Если в определителе имеются 2 одинаковые(пропорциональные) строки (столбца), то он равен 0.
4) Если элементы какой-либо строки (столбца) умножить на z, то определитель
умножится на z.
5) Если все элементы какой-либо строки (столбца) равны нулю, то он сам равен нулю.
6) Если к элементам какой-либо строки (столбца) прибавить соответственно элементы
другой строки (столбца), умноженные на z0, то определитель не изменится.
7) Сумма произведений элементов любой строки(столбца) определителя на соответствующие алгебраические дополнения этой строки(столбца) равна этому определителю.
8) Сумма произведений какой-либо строки(столбца) определителя на соответствующие алгебраические дополнения элементов любой другой строки(столбца) равна нулю.
5 ------------------------------------------
Элементарные преобразования матриц:
1) Перестановка двух столбцов(строк) определителя приводит к изменению его знака на противоположный.
2) Умножение всех элементов одного столбца(строки) определителя на одно и то же число, отличное от нуля, приводит к умножению определителя на это число.
3) Прибавление к элементам одного столбца(строки) определителя соответствующих элементов другого столбца, умноженных на одно и то же число, не изменяет определитель.
Лемма: При помощи элементарных преобразований только над строками(столбцами)
можно привести любую квадратную матрицу к теугольному виду.
Методы вычисления определителей:
Метод приведения к треугольному виду.
1. При помощи элементарных преобразований привести определитель к треугольному виду.
2. Вычислить определитель треугольного вида, перемножая его элементы, стоящие на главной диагонали.
Метод понижения порядка.
1. При помощи элементарных преобразований 3го типа нужно в одном столбце сделать равными нулю все элементы, за исключением одного.
2. Разложить определитель по этому столбцу(строке) и получить опеределитель меньшего порядк, чем исходный. Если его порядок > 1, то пункт 1, иначе закончить вычисления.
Метод изменения всех элементов определителя.
При вычислении определителя бывает полезно изменить все его элементы, умножив их на одно и то же число, не равное нулю, либо прибавить к каждому элементу одно и то же число.
Так же можно воспользоваться правило Сарриуса для матрицы порядка 3x3.
6 ------------------------------------------
Теорема о определителе произведения матриц:
Определитель произведения двух квадратных матриц равен произведению их определителей Доказательство: приведем матрицы к верхне треугольному виду, их детерминант стал равен произведению диаганальных элементов,теперь перемножим их, получили верхне диаганальную матрицу в которй элементы по диаганали равны произведению элементов стоящих на тех-же местах, т.е.(a11*a22*…*ann)*(b11*b22*…*bnn)=(a11*b11)*(a22*b22)*… (ann*bnn)
Следствие об определителе блочно-диагональной матрицы:
Определитель блочно-диаганальной матрицы равен произведению определителей блоков. (По диаганали стоят не нулевые матрицы)
7 ------------------------------------------
Обратная матрица:
Матрица
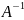 ,
удовлетворяющая вместе с заданной
матрицей А равенствам: А-1*А=А*А-1
,
удовлетворяющая вместе с заданной
матрицей А равенствам: А-1*А=А*А-1
=Е называется обратной.
Матрицу называют обратимой, если для нее существует обратная, иначе- необратимой.
A-1=1/detA *A+ , где А+ - матрица, транспонированная для матрицы, состоящей из алгебраических дополнений элементов матрицы А.
Матрица А+ называется присоединенной матрицей по отношению к матрице А.
Матрица 1/detA *A+ существует при условии,что detA не = 0.
Теорема о существовании и единственности обратной матрицы:
Теорема: Квадратная матрица nxn, с определителем, не равным нулю, имеет обратную матрицу, и притом только одну.
Доказательство. Надо показать,что А-1 обратная матрице А, т.е. удовлетворяет двум условиям:
1) A* (1/detA * A+)=E
2) (1/detA * A+) *A=E
Докажем первое равенство. Согласно свойству определителя следует, что А*А+=detA*E
Поэтому
A* (1/detA * A+)=1/detA* А*А+=1/detA* detA*E
=Е ч.т.д.
Аналогично доказывается второе равенство=> матрица А имеет обратную А-1=1/detA *A+
Единственность: Пусть кроме А-1 существует еще одна обратная матрица В(В не= А-1) такая, что АВ=Е. Умножим обе части этого равенства слева на матрицу А-1, то получим А-1АВ=А-1Е. Отсюда В=А-1, что противочерит условию=> обратная матрица единствена.
Свойства обратной матрицы: 1) (A-1)-1=A; 2) (AB)-1=A-1B-1; 3) (AT)-1=(A-1)T; 4) E=E-1;
8 ------------------------------------------
Матричные уравнения AX=B, YA=B:
Если определитель матрицы отличен от нуля, то матричное уравнение вида АХ=В имеет единственное решение Х=А-1В
AX=B (A-1*A)X=A-1*B т.к. (A-1*A)=E, то X=A-1*B.
Если определитель матрицы отличен от нуля, то матричное уравнение вида YA=В имеет единственное решение Y=BА-1
YA=B
Y=BA-1
AXB=C
X=A-1CB-1
Алгоритмы нахождения обратной матрицы:
I: 1) Вычислить det A. Если он равен нулю, то A-1 не существует;
2) Составляем матрицу (Aij) состоящую из алгебраических дополнений Aij=(-1)i+j*Mij элементов матрицы A;
3) Транспонируем матрицу (Аij) и получаем присоединенную матрицу А+=(Аij)T;
4) A-1=A+/detA
А-1= 1/detA * A+
II: 1) Запишем расширенную (A|E).
2) Элементарными преобразованиями над строками приведем эту расширенную матрицу к виду (E|B) (т.е. (A|E)(E|B)). Тогда B и будет обратной матрице A.
9 ------------------------------------------
Линейная зависимость и линейная независимость столбцов матрицы:
Столбец А называется ЛК столбцов A1Ak одинаковых размеров, если A=1A1++kAk , где 1k – коэфициенты линейной комбинации(некоторые числа). В этом случае говорят, что столбец А разложен по столбцам А1…Аk, а числа 1k называются коэффициентами разложения. Если коэффициенты разложения равны 0, то ЛК тривиальная.
Набор столбцов А1…Аk одинаковых размеров называется системой столбцов.
Система столбцов A1…Ak называется линейно-зависимой, если существуют числа 1k, не все равные нулю одновременно, такие, что если A=1A1++kAk=0, 0-нулевой столбец.
Система столбцов A1…Ak называется линейно-независимой, если равенство возможно только при 1==k=0, т.е. когда ЛК в левой части тривиальная.
Один столбец А1 тоже образует систему при А1=0 – ЛЗ, А1 не=0 – ЛНЗ
Любая часть системы столбцов называется подсистемой.
