Правило Крамера:

Если определитель ∆ матрицы системы n линейных уравнений с n неизвестными отличен от нуля, то система имеет единственное решение, которое находится по формулам xi=∆i/∆ , i=1,2…,n

Где ∆i- определитель матрицы, полученной из матрицы системы заменой i-го столбца столбцом свободных членов, то есть

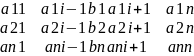
Если det A 0 (A-матрица системы), то система имеет решение X=A^-1b, где А^-1=1/∆ * A⁺

Xi=1/∆*(A1i*b1+A2i*b2+…+Ani*bn)

для нахождения очередного x надо заменить столбец с таким же номеров как у x на столбец b. Тогда x=detD/detA, где D – получившаяся после замены матрица.

16 -----------------------------------------

Теорема Кронекера-Капелли:

Система линейных уравнений совместна тогда и только тогда, когда rg A = rg (A|B). (Следствие: если ранг совместной системы равен числу неизвестных, то она имеет единственное решение, иначе бесконечно много).

Рассмотрим систему m линейных уравнений с n неизвестными. Составим блочную матрицу, приписав к матрице А справа столбец свободных членов и получим расширенную матрицу системы (А|b).

Доказательство: необходимость - Доказательство: x= - реш. сис-мы. Если

Система имеет решения,то столбец свободных членов есть ЛК столбцов матрицы системы. Поэтому при вычеркивании столбца b bp расширенной матрицы(А|b) ее ранг не изменится=> rg(A|b)=rgA

Достаточно: базисный минор A является базисным минором расширенной матрицы поэтому b не входит в базисный минор матрицы по теореме о базисном миноре столбец B является линейной комбинацией столбцов базисного минора матрицы А => всех столбцов матрицы A ч.т.д.

rgA=rg(A|b) система совместна(из ступ. вида)

rg(A|b)=r

a)r=n –единственное решение

б)r<n – бесконечно много решений(система не определена)

Алгоритм (Гаусса) решения неоднородной системы:

Метод Гаусса – последовательное исключение неизвестных. Он происходит в два действия(хода - прямой и обратный). Прямой заключается в привидении матрицы к ступенчатому виду(работа только со строками матрицы). Если RgA=Rg(A|B), то можно приступать ко второму шагу. Обратный ход заключается в выражении неизвестных через другие (начиная с последнего уравнения), подстановке в следующее (верхнее уравнение), тем самым нахождение всех неизвестных по очереди.

1)Составить расширенную матрицу системы

2)Привести к ступенчатому виду матрицу (А|b)

3)Проверить на совместность матрицы А и (А|b), если rgA=rg(A|b) совместна,иначе-нет решений.

4)Привести матрицу (А|b) к простейшему виду

5)Разделить переменные на свободные и базисные

Если все неизвестные х1,х2,…,хn будут базисными,то единственное решение x1=b1,x2=b2,xn=bn

6)Находим частное решение(свободные переменные обнуляются)

7)Находим Общее решение однородной системы(выражаем базисные переменные через свободные)

Находим ФСР(свободные переменные приравниваем к нулю,кроме одной равной 1)

Например х1 х2 х3 х4 х5

h1 1 0

h2 0 1

Ответ: x^ч + с1( )+с2( )

17-----------------------------------------

Однородная система линейных уравнений

или Ах=0

Всегда совместна, т.к. имеет тривиальное решение х1=х2=….=xn=0

Если ранг матрицы равен количеству неизвестных, то решение единственное.

Любая совокупность ЛНЗ решений однородной системы называется ФСР.

Общее решение однородной системы есть любая совокупность столбцов ФСР.

Свойства решений однородной системы

1)Если столбцы u1,u2,…uk- решения однородной системы,то любая их ЛК α1u1+ α2u2+…+ αkuk так же является решением однородной системы.

Если ранг матрицы однородной системы равен r, то она имеет n-r ЛНЗ решений.

Нахождение ОРОС

1)Ступенчатый вид

2)rgA=r=>r базисных перемнных,n-r свободных

3)Найти ФСР u1,u2,…un-r однородной системы.Для этого подставить в последовательность n-r стандартных наборов значения свободных переменных, в которых все свобобные переменные равны нулю,кроме одной,равной 1.

х1 х2 х3 х4 х5

h1 1 0

h2 0 1

х^o = с1( )+с2( )

18 -------------------------------------

ОРНОС=ЧРНОС+ОРОС

Алгоритм решения неоднородной системы

1)(А|b) к ступенчатому виду

2)Пусть ранг (A|b) равен r; б.п. , св.п.

3)ЧР(свободные переменные=0)

4)Ах=> ФСР =х^о

5)х=х^ч+х^о

======= ТЕМА 2 =======

19 -----------------------------------------Векторы:

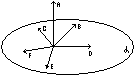
Векторы b, c, d, e, f – компланарны, а вектор а c любыми двумя некомпланарны.

Коллинеарными называются вектора лежащие на одной прямой.

Компланарными называются вектора лежащие в одной плоскости.

Вектор - направленный отрезок – упорядоченная пара точек P и Q пространства, где P – начало направленного отрезка – точка приложения вектора , а Q – его конец(обозначение PQ). Вектор, начало и конец которого совпадают называется нулевым. Направление нулевого вектора не определено. Расстояние между точками A и B называют длинной или модулем вектора(|AB|).

Определение(равенство векторов AB=CD):

A=B и C=D (т.е. AB и CD нулевые векторы)

векторы не единичны, лежат на одной прямой, имеют одинаковую длину и направление.

A, B, C, D – разные точки, никакие три из них не лежат на одной прямой, AB||CD и AC||BD. Обладают следующими свойствами:

Если AB=CD, то CD=AB.

Если AB=CD и CD=EF, тогда AB=EF.

Если AB=CD, то |AB|=|CD|.

Для любых трех точек A, B и C существует единственная точка D такая, что: AB=CD.

Линейные операции над векторами:

A) Сложение векторов: Если u₁ и u₂ два свободных вектора, то приложим их к какой-нибудь точке O. Получившийся вектор OB называется их суммой, т.е. OB=OA+AB.

B) Произведением ненулевого вектора а на действительное число ( не=0) называется вектор *а,удовлетворяющий условиям:

1)длина вектора *а равна ||*|a|, т.е |a|=||*|a|

2)векторы *а и а коллинеарные(*а || a)

3)векторы *а и а одинаково направлены, если  > 0, и противоположно направлены при <0

4)деление ветора на отличное от нуля число u сводится к его умножению на число =1/u

5)при делении ненулевого вектора а на его длину,получается единичный вектор е,одинаково направленный с а.

6)при умножении единичного вектора на число  получаем коллинеарный ему вектор, длина которого равна ||.

Свойства линейных операций

1)а+b=b+a коммутативность

2)(a+b)+c=a+(b+c) ассоциативность

3)а+0=а

4)а+(-а)=0

5)(αβ)*а= α*(βа) ассоциативность

6) (α+β)*а=αа+βа дистрибутивность

7)α(а+b)=αa+αb дистрибутивность

8)1*а=а

Базис на прямой – обыкновенный вектор.

Базис на плоскости – два неколлинеарных вектора e1, e2, данных в определенном порядке и приложенных к точке О – началу базиса.

Базис в пространстве – тройка некомпланарных векторов e1, e2, e3, данных в определенном порядке и приложенных к точке О – началу базиса.

Базис называется ортонормированным, если его векторы попарно ортогональны и по величине равны единицы.

Теорема: В ортонормированном базисе:

Если a=(x_a;y_a;z_a), и b=(x_b;y_b;z_b) тогда c=(a;b)=x_ax_b+y_ay_b+z_az_b;

Доказательство(левое какое-то):

(a;b)=x_ax_b(i;i) + y_ay_b(j;j) + z_az_b(k;k) = x_ax_b+y_ay_b+z_az_b, т.к. (i;i)= (j;j)= (k;k)=1. Ч.Т.Д.

Теорема о разложении вектора по базису:

Любой вектор a может быть единственным образом разложен на сумму трех векторов, параллельным трем данным некомпланарным векторам - по базису.

a=u+v+w, где u,v,w – компоненты, а ,,-коэффициенты этого разложения.

20------------------------------------------

Линейная зависимость и независимость векторов:

Линейной комбинацией векторов u₁,…, u_n с коэффициентами a₁, …, a_n называется вектор a₁u₁+…..+a_nu_n.

Линейная комбинация векторов a₁u₁+…+a_nu_n называется нетривиальной, если в ней хотя бы один из коэффициентов a₁, …,a_n отличен от нуля. В противном случаи она тривиальна и равна нулевому вектору.

Система векторов u₁,…,u_n называется линейно зависимой, если существует хотя бы одна нетривиальная комбинация этих векторов, равная нулю. Утверждения о линейной зависимости:

Если среди векторов u₁,…, u_n есть хотя бы один нулевой вектор, то вся система векторов линейно зависима.

Если среди векторов u₁,…,u_n некоторые образуют линейно зависимую систему, то и вся система u₁,…,_un линейно зависима.

Если система u₁…,u_n линейно зависима, то по крайней мере один из векторов u₁…,u_n равен линейной комбинации остальных.

Геометрический смысл линейно зависимых векторов заключается в следующем:

система, состоящая из двух векторов, линейно зависима тогда и только тогда, когда векторы коллинеарны.

система, состоящая из трех векторов, линейно зависима тогда и только тогда, когда векторы компланарны.

всякие четыре вектора в пространстве линейно зависимы.

Векторное многообразие есть такое непустое множество V векторов, что любая линейная комбинация векторов принадлежит этому множеству. Размерность V может быть ровна 0(состоит из одного нулевого вектора),1(состоит из всех векторов, коллинеарных какой-либо прямой), 2(состоит из всех векторов, ком планарных некоторой плоскости), 3(состоит их всех вообще векторов трехмерного пространства).

Любое семейство векторов, содержащее нулевой вектор, линейно независимо.

21------------------------------------------