
- •Постановка задачи
- •Конечные разности различных порядков
- •Символ будем рассматривать как оператор, ставящий в соответствие функции f(X) разность
- •6. Обобщенной n-степенью числа X с шагом h называют произведение
- •7. Первая интерполяционная формула Ньютона
- •Лекция 3. Вторая интерполяционная формула Ньютона. Формула Лагранжа. Схема Эйткена
- •Вторая интерполяционная формула Ньютона
- •Интерполяционная формула Лагранжа
- •Интерполирование по схеме Эйткена
Лекция 2. Интерполирование функций
Постановка задачи
Пусть на отрезке [a,b]
оси Х заданы (n+1) точка
![]() ,
которые называются узлами интерполяции
и заданы значения
,
которые называются узлами интерполяции
и заданы значения
![]() некоторой функции y=f(x)
в этих точках
некоторой функции y=f(x)
в этих точках
![]() .
.
a
b







![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Требуется построить функцию F(x) (интерполирующую функцию), принадлежащую к определенному классу и принимающую в узлах интерполяции те же значения, что и f(x)
![]()
Геометрическая интерпретация (см. рис.)
В такой общей постановке задача может не иметь решения (например, 3 точки и прямая линия). Задача имеет единственное решение в классе полиномов степени n и много решений в классе полиномов степени выше n:
- практическое значение задачи интерполяции
- отличие экстраполирования от интерполирования.
Сужаем задачу:
а) в качестве интерполирующей функции
примем полином степени n,
проходящий через точки
![]() ;
;
б)
![]()
Конечные разности различных порядков
Пусть y=f(x),
![]()
![]() - первая конечная разность функции f(x)
- первая конечная разность функции f(x)
![]()
Например,
![]()
Пример 1
![]()

Пример 2
Для
![]() получим таблицу
получим таблицу
x |
y |
|
|
|
x |
|
(e-1) |
|
|
x+1 |
|
(e-1) |
|
|
x+2 |
|
(e-1) |
|
|
x+3 |
|
|
|
|
Символ будем рассматривать как оператор, ставящий в соответствие функции f(X) разность
Свойства оператора
а)
![]()
б)
![]()
в)
![]()
г)
![]() - по определению
- по определению
![]() ,
где Е – символ
,
где Е – символ


4.
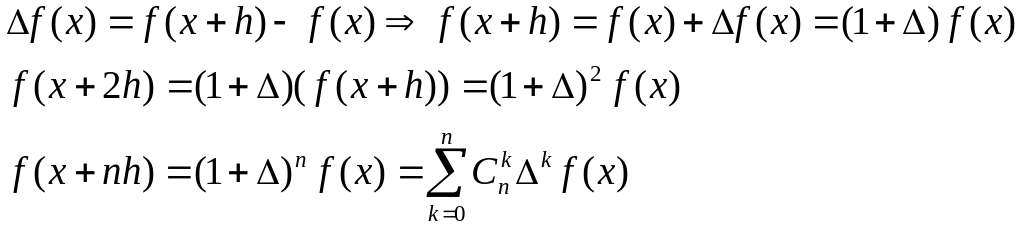 (4) (последовательные
значения)
(4) (последовательные
значения)
Последовательные значения f(x) формулой (4) выражаются конечными разностями последовательных порядков функции f в точке x.
5.
![]()
![]()
![]() (5)
(5)
Последовательные разности функции f(x) в точке x формулой (5) выражаются через ее последовательные значения
6. Обобщенной n-степенью числа X с шагом h называют произведение
![]()
Если h=0, то обобщенная n – степень равна обычной
![]()
Найдем последовательные разности обобщенной степени


![]() конечная разность 1-го
порядка
конечная разность 1-го
порядка
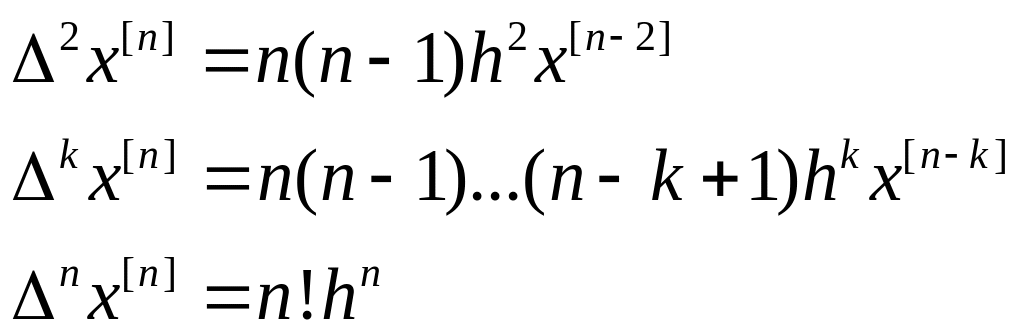
![]() ,
если m > n
,
если m > n
7. Первая интерполяционная формула Ньютона
Дано
![]()
Требуется найти полином
![]() степени n, для которого
степени n, для которого
![]()
При этом
![]()
Ищем полином в виде
![]()
=![]()
![]()
![]()

![]()
![]()
Отсюда
![]()
Пусть
![]() ,
,
тогда 1-ая интерполяционная формула Ньютона
![]()
8. Пример
x |
y |
|
|
|
3,50 |
33,115 |
1,698 |
0,087 |
0,005 |
3,55 |
34,813 |
1,785 |
0,092 |
0,003 |
3,60 |
36,598 |
1,877 |
0,095 |
- |
3.65 |
38,475 |
1,972 |
- |
- |
3,70 |
40,447 |
- |
- |
- |
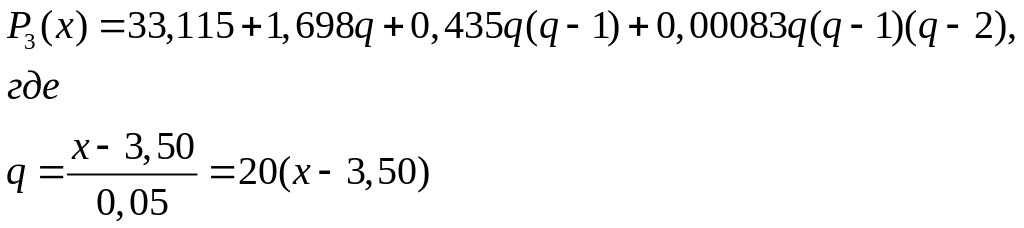
Пусть q=0,4, что соответствует x=3,52
x |
q |
|
|
|
|
3,52 |
0,40 |
33,784 |
33,79420 |
33,78376 |
33,78408 |
