Лекция 3. Вторая интерполяционная формула Ньютона. Формула Лагранжа. Схема Эйткена

Напомним 1-ую интерполяционную формулу Ньютона

Первую интерполяционную формулу Ньютона используют для интерполирования вперед или экстраполирования назад, если x между и ( ).

Вторая интерполяционная формула Ньютона

Дано

Будем искать интерполяционный полином в виде

, (3)

где - неопределенные коэффициенты

Будем искать из условия

Для этого достаточно чтобы

или

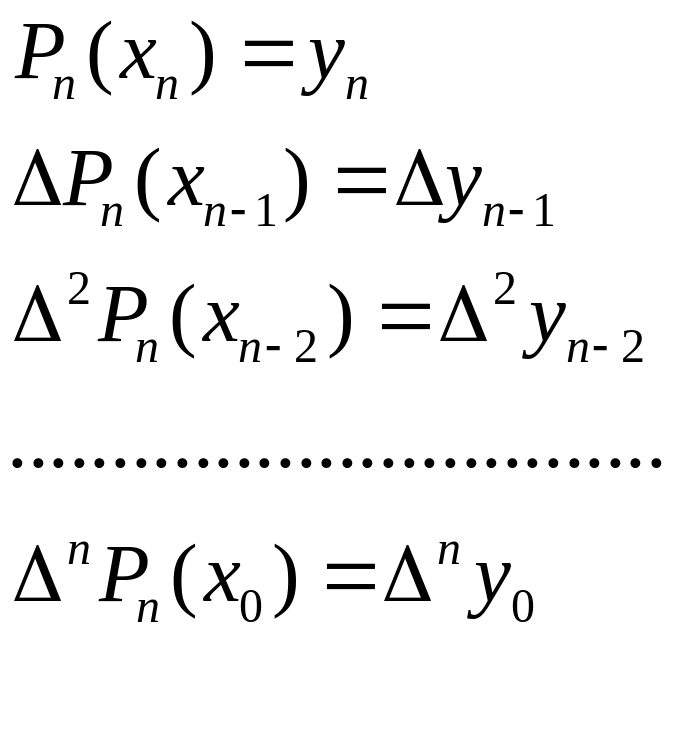
Положим в (3) , тогда

Возьмем разность 1-го порядка от левой и правой частей

Положим , тогда

Найдем разность 2-го порядка

Положим , тогда

П о аналогии

Вторая интерполяционная формула Ньютона:

Пусть

Тогда

Вторую интерполяционную формулу Ньютона используют для интерполирования назад или экстраполирования вперед.

Пример построения интерполирующего полинома для функции y=lg x,

x	y(x)
1000	3,0000000	0,0043214	-0,0000426	0,0000008
1010	3,0043214	0,0042788	-0,0000418	0,0000009
1020	3,0086002	0,0042370	-0,0000409	0,0000008
1030	3,0128372	0,0041961	-0,0000401
1040	3,0170333	0,0041560
1050	3,0211893

3,0211893 + 0,0041560q - 0,0000200q(q+1) + 0,0000001q(q+1)(q+2)

Пусть x=1044, тогда

x	lg x
1044	3,0187005	3,0186957	-0,0000048	3,0187005	0

Интерполяционная формула Лагранжа

(для равно- и неравноотстоящих значений аргумента)

Дано

Требуется построить полином

Решим сначала частичную задачу

Построить полином n-го порядка |

- символ Кронкера

Так как - корни ( ) полинома , то

- (теорема Виета)

Из условия , найдем

Следовательно

i=0,1,…,n

Тогда

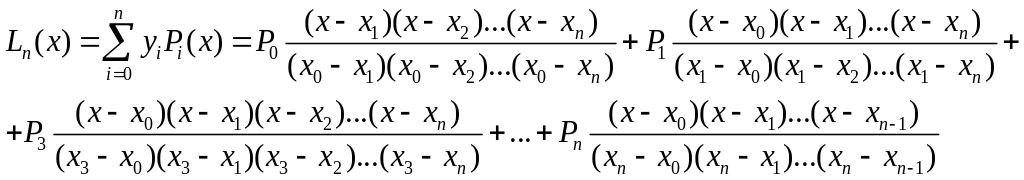
Если аргументы равноотстоят

, то формула Лагранжа, для имеет вид

Для коэффициентов составим таблицы

Оценка погрешности интерполяции

Интерполирование по схеме Эйткена

Это один из современных способов решения задачи интерполирования, реализуемый на ЭВМ.

Работает, как при равномерной так и не равномерной сети значений аргумента x таблично заданной функции.

Обозначим - интерполяционный полином степени n с графиком, проходящим через (n+1) точку ,

В этой записи имеется в виду, что

(1)

Нас будет интересовать значения интерполяционного полинома при произвольном не табличном значении x.

Основные рабочие формулы Эйткена имеют вид:

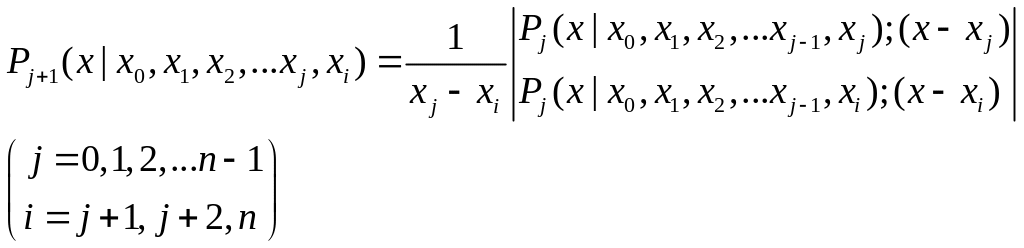(2)

В правой части (2) стоит определитель 2-го порядка одной и той же структуры для всех значений i и j.

Рассмотрим работу формул Эйткена для случая j=0. В этом случае с учетом (1) формула (2) приобретает вид

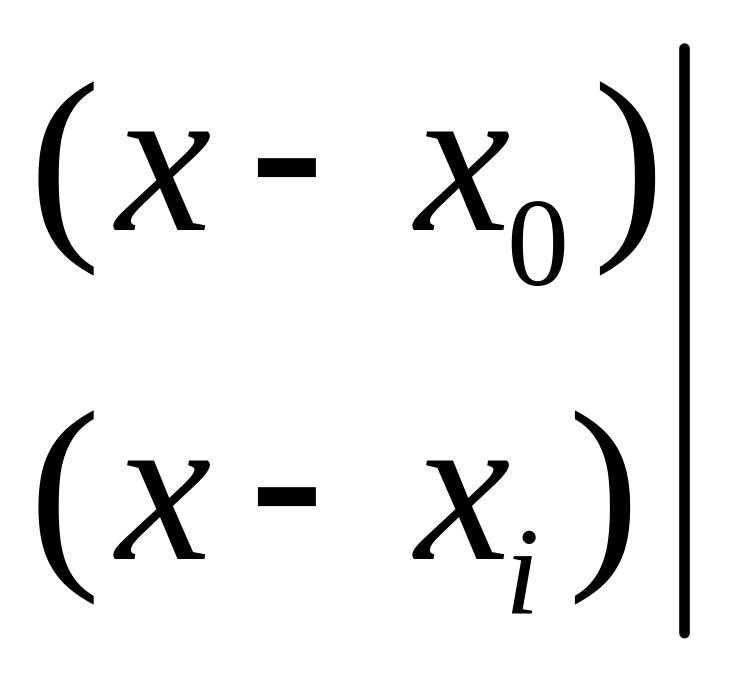
(3)

Правая часть (3) показывает, что полином действительно является некоторым полиномом 1-го порядка. Его значение при равно

Его значение при i=1,2,..n равно

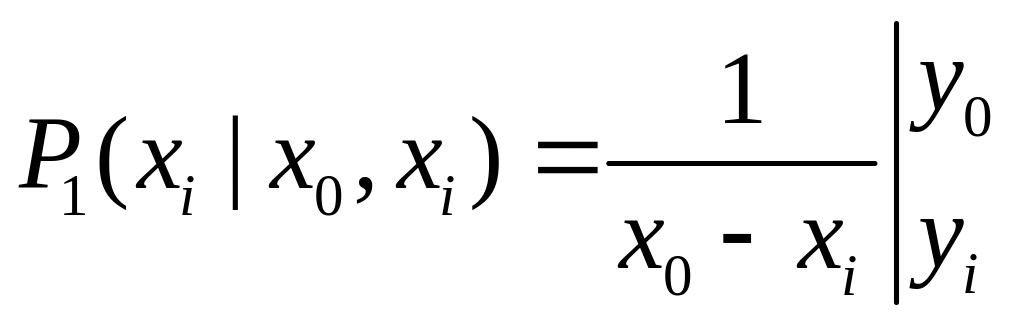
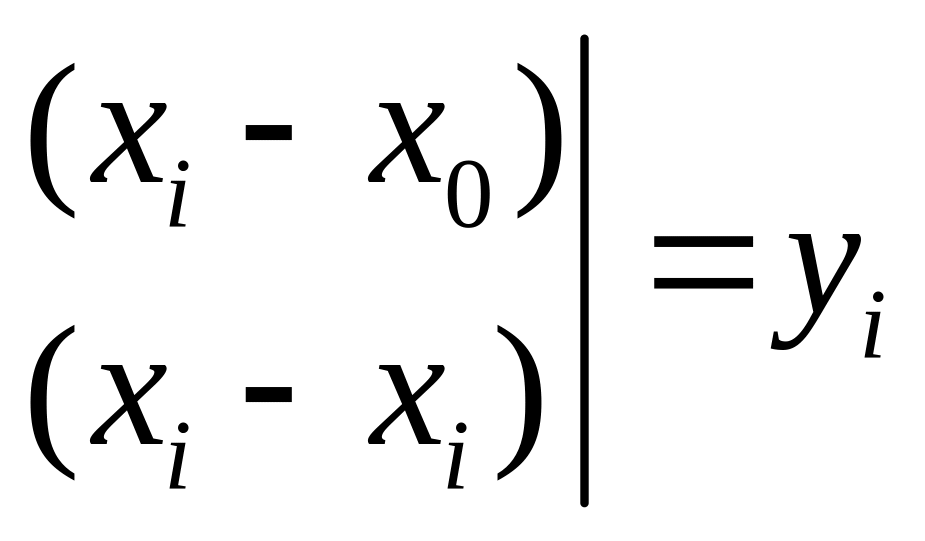
Следовательно, полином действительно является интерполяционным полиномом 1-й степени, график которого проходит через две точки и , ( ).

Выполнив вычисления по формуле (3) циклом по , мы получим значения 1-го столбца в определителе правой части формулы (2) для случая j=1.

Пусть теперь j=1. В этом случае формулы (2) приобретают вид:

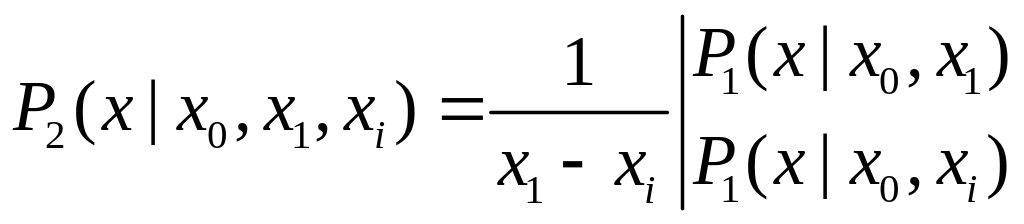
(4)

Заметим, что первый столбец в правой части (4) заполнен числами, которые уже вычислены на предыдущем этапе работы алгоритма при j=0.

Из (4) видно, что является некоторым полиномом 2-й степени. Его значение, при равно

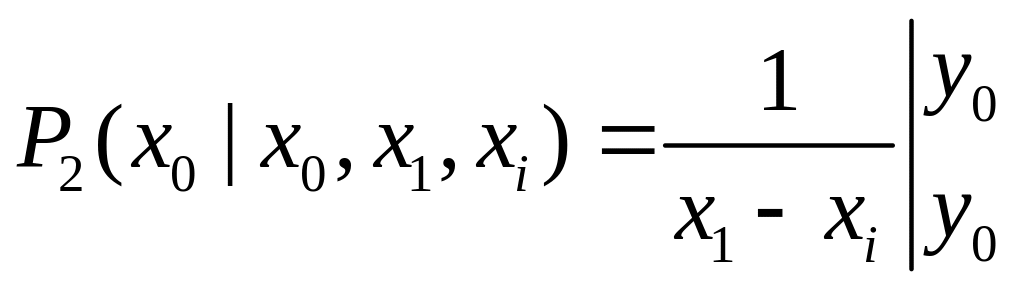
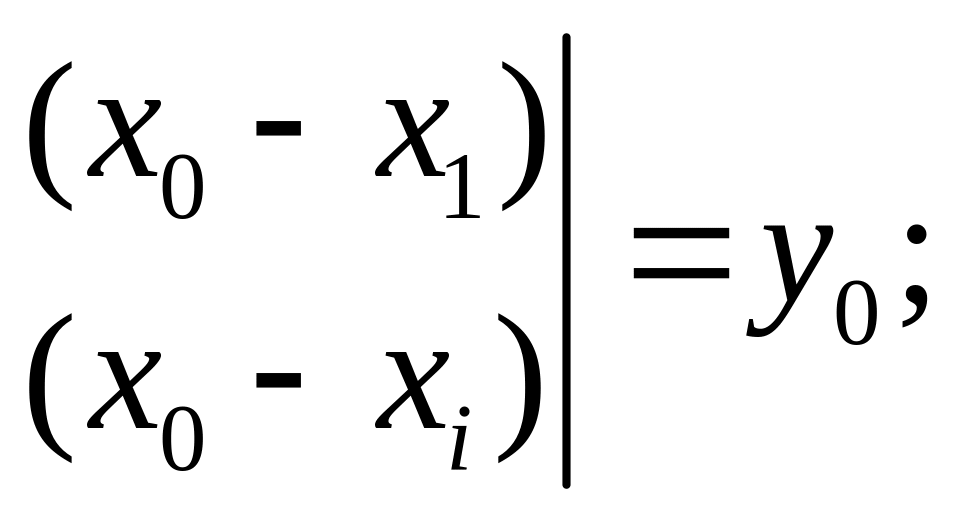
При

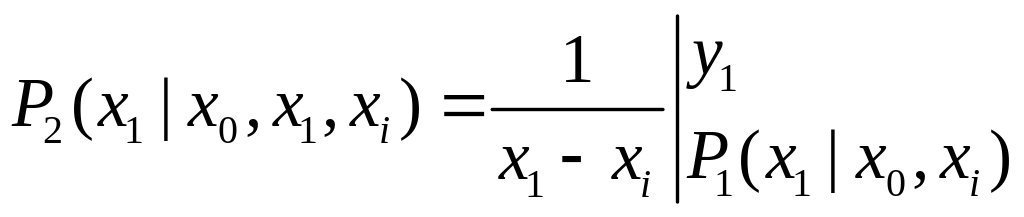
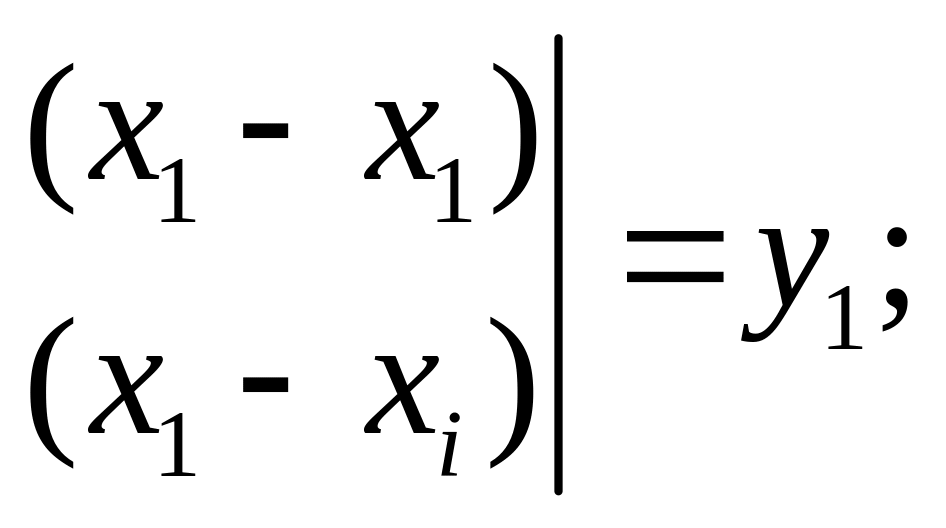
При

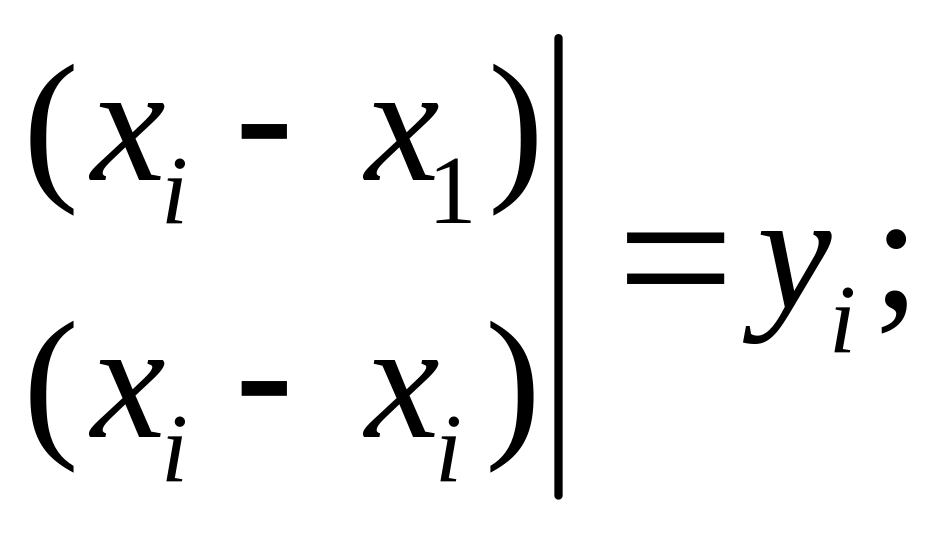
Следовательно, полином действительно является интерполяционным полиномом 2-го порядка, график которого проходит через три табличные точки , и , ( ). Выполнив по формулам (4) цикл при , мы получим значения 1-го столбца в определителе правой части формулы (2) для случая j =2.

Продолжим рост индекса j. Пусть мы уже нашли для всех предыдущих значений j величины

Тогда формулы Эйткена для общего случая имеют вид:

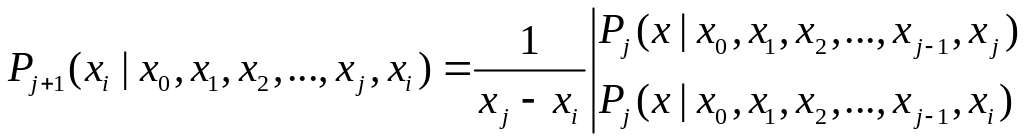
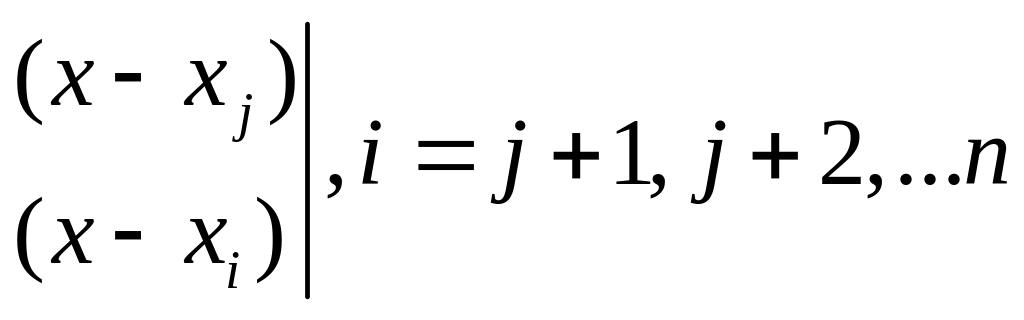
Из этой формулы видно, что полином является некоторым полиномом степени (j+1), как произведение полиномов степени j на биномы 1-й степени. Его значения при равны

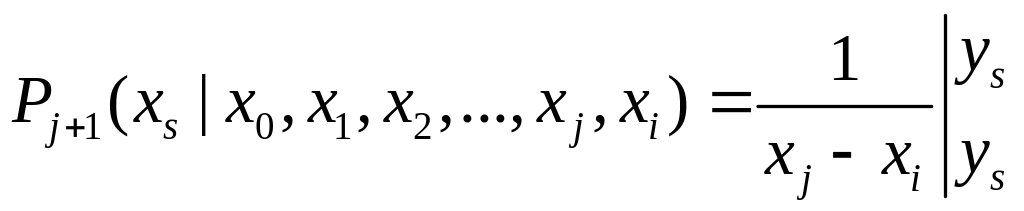
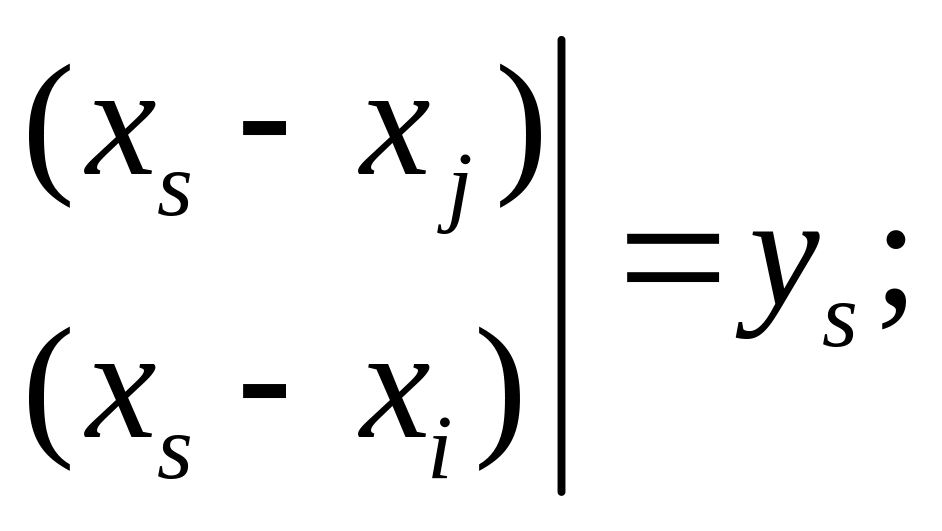при

Его значение, при

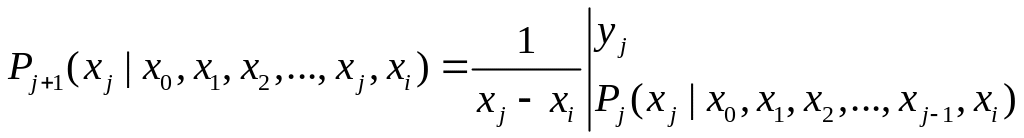
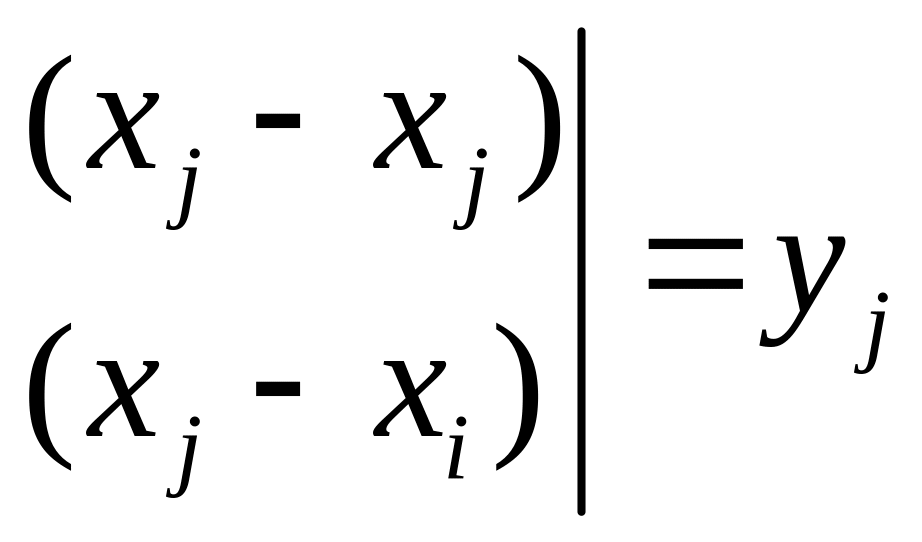
Его значение, при

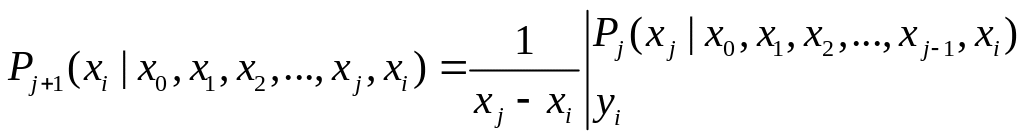
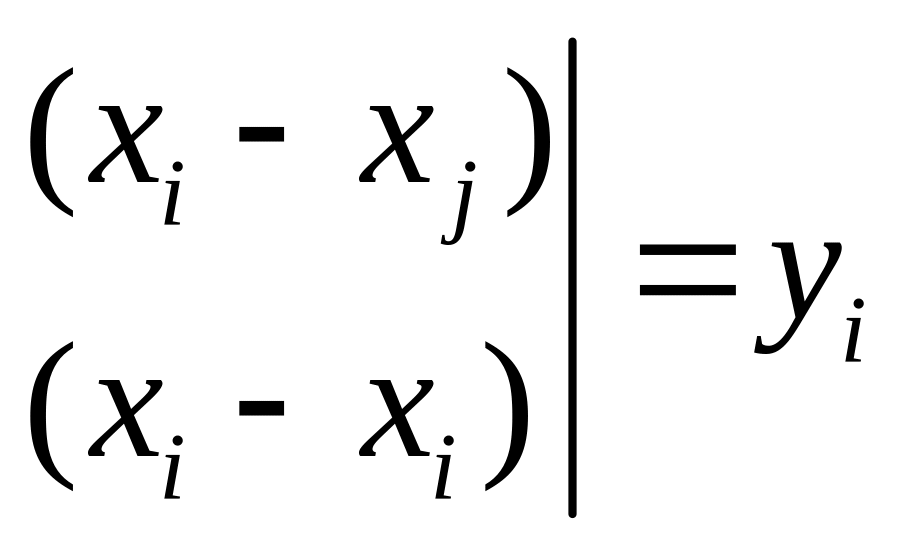
Следовательно, полином действительно является интерполяционным полиномом, график которого проходит через (j+2) точки

, , …, , ,

Выполнив двойной цикл вычислений по формуле (2) сначала по индексу , а затем внутри по циклу , мы получим искомое значение полинома степени , которое является решением поставленной выше задачи интерполирования.

Таким образом, все вычисления для решения задачи интерполирования таблично заданной функции сводятся к одному оператору двойного цикла с вычислением по одной и той же формуле, у которой всякий раз первый столбец определителя 2=го порядка заменяется на ранее вычисленные значения.

Перейдем к обсуждению способов решения задачи обратной интерполяции.

Эта задача ставится следующим образом:

Задана табличная функция и не табличное значение y.

Требуется найти такое значение x, при котором не табличное значение интерполяционного полинома равно заданному значению y (найти ).

Рассмотрим случай равномерной сети табличных значений аргумента x.

В этом случае интерполяционный полином может быть представлен одной из интерполяционных формул Ньютона. Для определенности, пусть это будет 1-ая

интерполяционная формула Ньютона. Пусть степень полинома будет n=4 (из практических занятий вы уже знаете, что рациональная степень интерполяционного полинома редко превышает n=4).

Тогда

(5)

Здесь величина y известна, а значение является неизвестным. Уравнение (5) относительно переменной q является нелинейным алгебраическим уравнением 4-й степени, и поиск его корней является весьма сложной задачей.

Будем искать корень этого уравнения методом итераций. После деления уравнения (5) на , преобразуем его к виду:

(6)

В качестве начального приближения к корню уравнения (6) примем значение

(7)

а все последующие приближения будем получать итерациями:

(8)

Если процесс итераций сходится, то корень получится как предел

(9)