14.2. Линейная модель обмена (модель международной торговли)

Рассмотрим n стран (n N): S₁, S₂, ..., S_i, ..., S_n с известным национальным доходом x₁, x₂,..., x_i, ..., x_n соответственно.

Пусть a_ij - запланированная доля национального дохода страны S_j на покупку товаров у страны S_i, ( ). Числа a_ij можно записать в виде матрицы

.

В этой задаче квадратную матрицу А называют структурной матрицей торговли.

Будем считать, что весь национальный доход каждой страны S_i используется только на закупку товаров либо внутри самой страны ( ), либо на импорт из других стран ( ) . Естественно, что в матрице А элементы неотрицательны и в каждом столбце сумма всех элементов равна единице.

Из перечисленных выше условий следует, что сбалансированная торговля возможна только при условии . При получим систему линейных уравнений, которую в матричной форме можно записать как (*) , где А -структурная матрица торговли, а 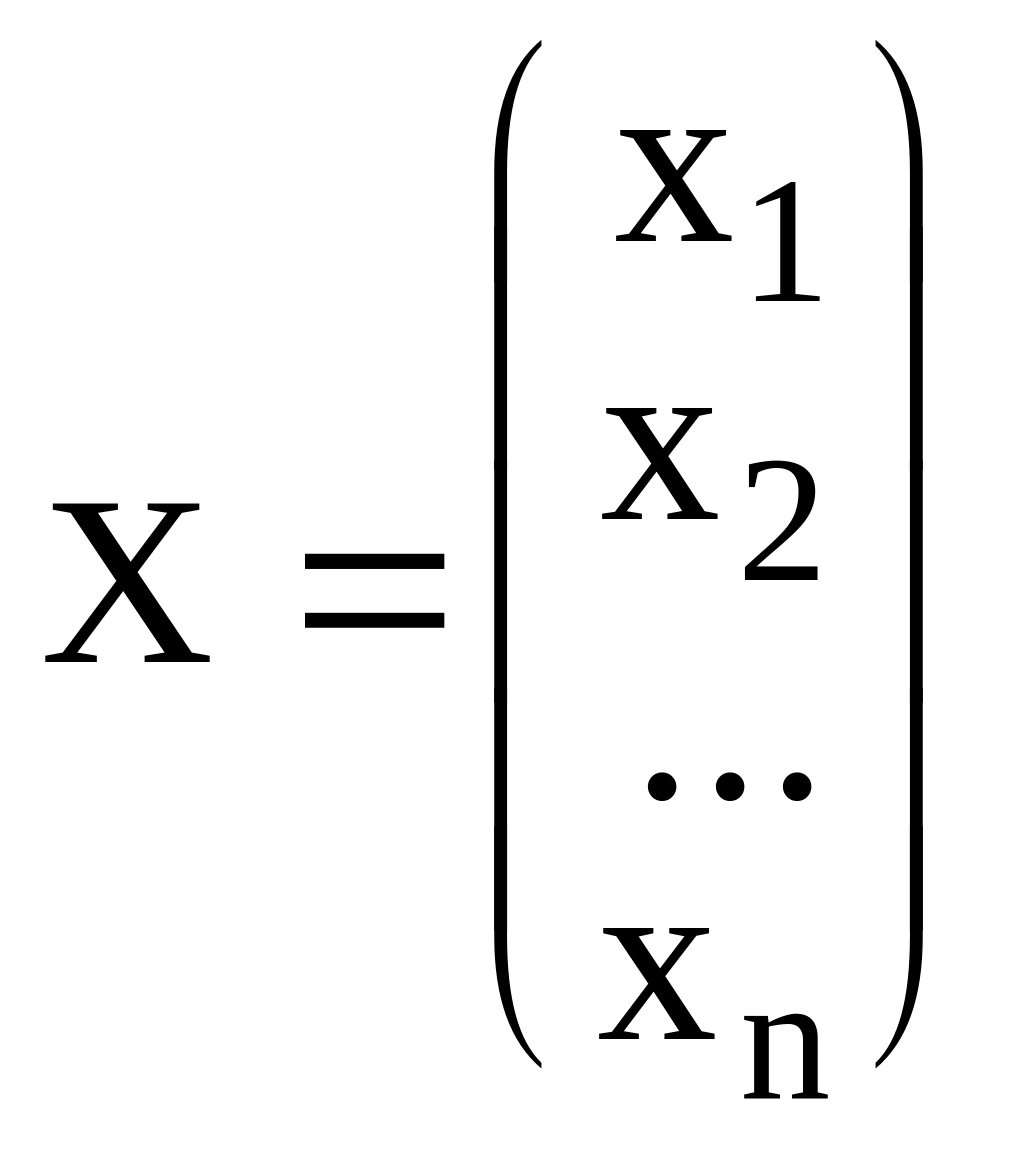- вектор национальных доходов по странам.

Из уравнения следует, что вектор Х можно рассматривать, как собственный вектор матрицы А с собственным числом . Следовательно, только собственный вектор структурной матрицы торговли с собственным числом даст национальные доходы стран, обеспечивающие сбалансированность торговли.

Пример.

Дана структурная мат рица торговли трех стран: .

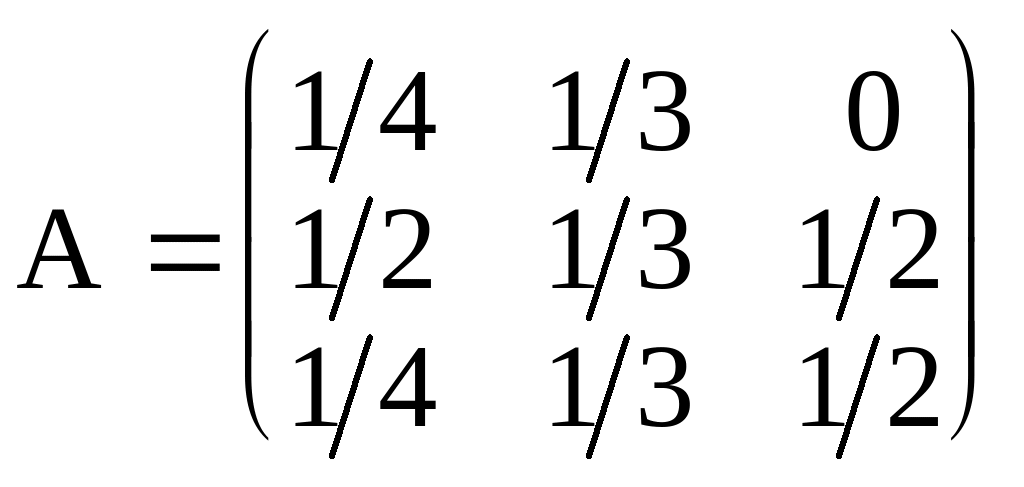Определить, при каких национальных доходах этих стран торговля между ними будет сбалансированной.

Найдем собственный вектор матрица А при . Для этого достаточно найти вектор Х из матричного уравнения . .

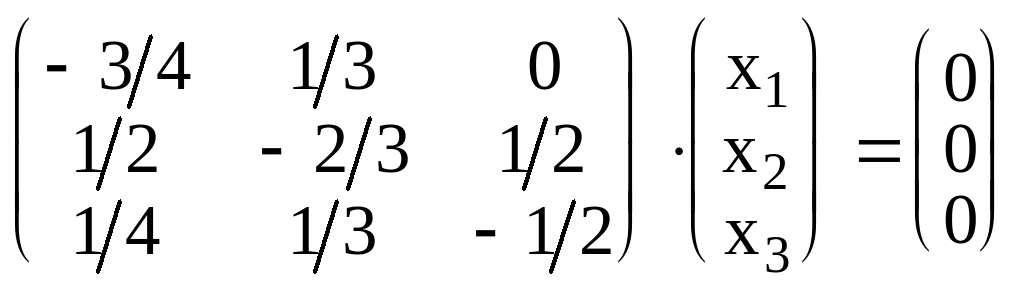. После умножения всех уравнений на 12 расширенная матрица этой системы будет иметь вид: .

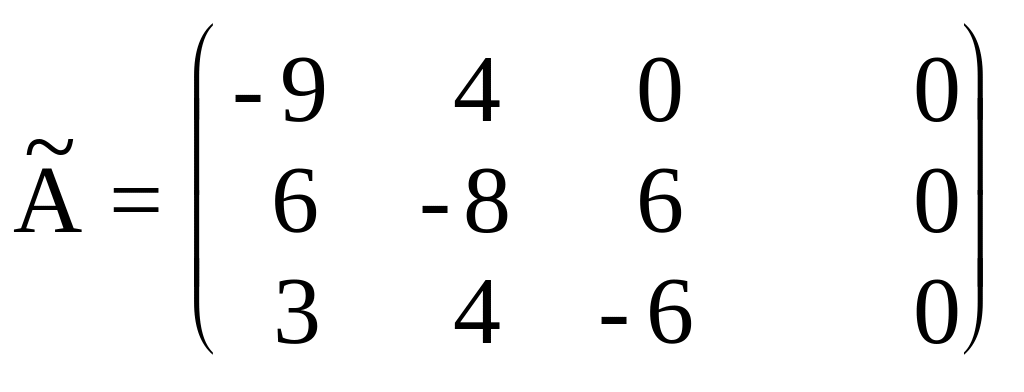Метод полного исключения приводит к результатам:

.

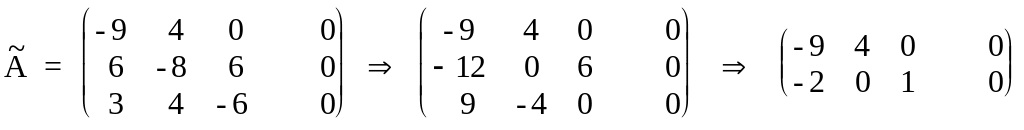Получили однородную систему двух линейных уравнений с тремя неизвестными. Однородная система всегда разрешима. Количество неизвестных равно 3, а ранг расширенной матрицы и матрицы системы равен 2, следовательно система имеет бесчисленное множество решений, зависящих от оного параметра ( 3-2=1 ) .

Пусть x₁ =4t, тогда x₂ =9t, x₃ = 2t, где t - параметр. Это означает, что при данной структурной матрице торговля будет сбалансированной только при условии, что отношение национальных доходов этих стран будет 4 : 9 : 2.

Оглавление

Глава		Стр.
	Литература	2
	Основные обозначения	3
1	Числовые множества	4
2	Векторы в геометрической форме	6
3	Метод координат	9
4	Умножение векторов	14
5	Матрицы	16
6	Определители	19
7	Обращение квадратной матрицы	21
8	Ранг матрицы	22
9	Системы линейных уравнений	23
10	Векторы в координатной форме	25
11	Комплексные числа	27
12	Векторное n-мерное пространство	30
13	Собственные числа и собственные векторы	34
14	Векторы и системы линейных уравнений в экономике	36
	Оглавление	40

37