58. Вывести правила дифференцирования постоянной, суммы, произведения. Примеры.

59. Вывести правила дифференцирования сложной функции. Примеры.

60. Рассказать о дифференцировании функций, заданных неявно и параметрически. Логарифмическое дифференцирование. Примеры.

Функция называется заданной параметрически, если переменные x и y зависят от некоторого общего аргумента t.

Воспользуемся определением производной, как отношением дифференциалов

.

Пусть функция имеет вид y=[u(x)]^v(x), т.е. является степенно-показательной. В этом случае для нахождения производной ее удобно прологарифмировать.

Аналогично поступаем, если функция содержит большое число сомножителей и определителей. Её удобно предварительно прологарифмировать.

61. Дать определение производных высших порядков. Доказать их основные свойства. Сформулировать правило Лейбница. Примеры.

Пусть функция y=y(x)- дифференцируема в некоторой области. ЕЕ производная в свою очередь является функцией от x; возможно, что она также дифференцируема, в этом случае производная от функции называется второй производной от функции y, т.е.

Совершенно логично можно определить производную любого порядка, а именно

Свойства высших производных:

1)

2)

3) Правило Лейбница.

62. Доказать теоремы Ферма и Ролля.

Теорема Ферма.

Пусть точка x₀ – точка локального экстремума. Если y(x) дифференцируема в окрестности x₀, то x₀ – стационарная точка, т.е. .

Доказательство.

Пусть x₀ – точка локального максимума. Составим разностное отношение и проанализируем его знак

Устремим теперь к нулю, т.е. , тогда по теореме о переходе к пределу в неравенствах мы имеем

Но т.к. функция дифференцируема, то

Что и требовалось доказать.

Теорема Ролля.

Пусть функция y=y(x)

1. непрерывна на [a;b]

2. дифференцируема внутри (a;b)

3. значения на концах интервала равны y(a)=y(b)

Тогда

Доказательство.

Т.к. функция y(x) непрерывна на замкнутом интервале, то она достигает на нем своего наименьшего и наибольшего значений. При этом возможно 2 случая:

1) m=M

2)m<M

В этом случае локальный экстремум достигается внутри интервала, а значит по теореме Ферма

Замечание: Если какое0нибудь из условий теоремы Ферма не выполнено, то ее утверждение может быть несправедливо.

63. Доказать теоремы Лагранжа и Коши. Физический и геометрический смысл теоремы Лагранжа.

Теорема Лагранжа.

Пусть функция y=y(x)

1)непрерывна на [a,b]

2) дифференцируема на (a;b)

Тогда

Теорема Ролля является частным случаем теоремы Лагранжа.

Теорема Коши.

Рассмотрим 2 функции y=f(x) и y=g(x) и пусть

1. f(x), g(x) непрерывны на [a;b];

2. f(x), g(x) дифференцируемы на (a;b);

3. 

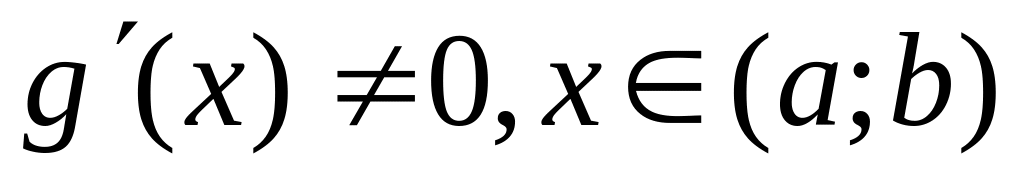
Тогда

Теорема Лагранжа является частным случаем теоремы Коши при g(x)=x.

Доказательство.

Из условия следует, что , в противном случае функция g(x) удовлетворяла бы всем условиям теоремы Ролля и нашлась бы точка C, в которой а это не верно по 3 условию теоремы.

Введем вспомогательную функцию

и подберем параметр так, чтобы функция F(x) удовлетворяла бы условию теоремы Ролля.

При некотором значении параметра , т.е.

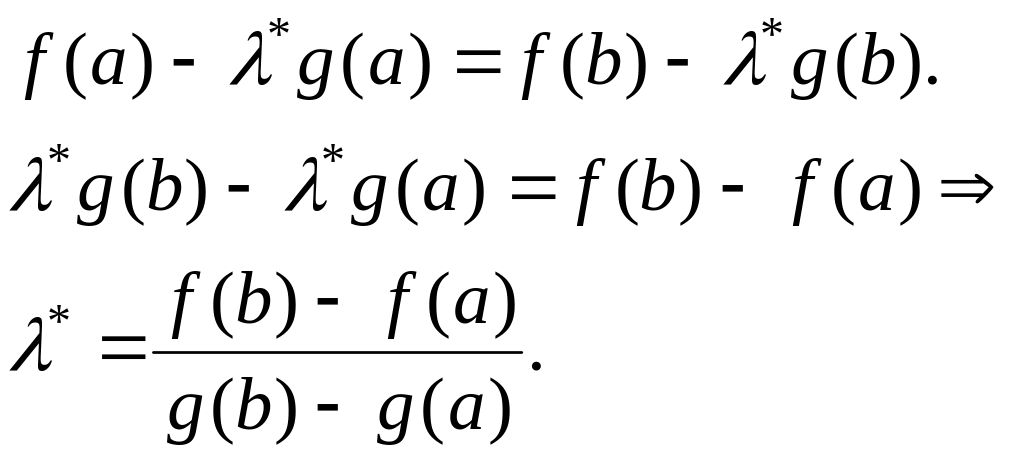
Для функции выполнены все условия теоремы Ролля, поэтому

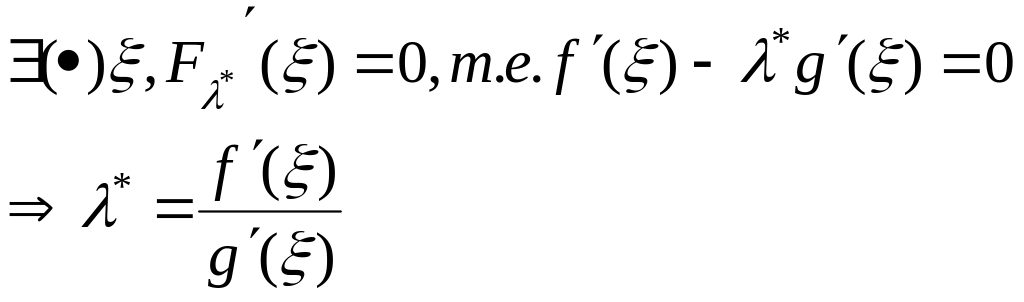
Приравняв , получим теорему Коши, а значит и теорему Лагранжа.

Физическая и геометрическая интерпретация теоремы Лагранжа.

Теорема Лагранжа может быть записана в виде

В этом виде оно называется формулой конечных приращений или иначе

Если x-время, а y(x) – путь, то и тогда эта формула звучит так:

Если функция зависимости пути от времени непрерывна и дифференцируема, то найдется такая точка, в которой мгновенная скорость равна средней.

Если выполнены условия теоремы Лагранжа, то найдется точка C, в которой касательная параллельна хорде.

64. Вывести формулу Тейлора.

Замена приращения функции ее дифференциалов служит источником многих приближенных формул. Эти формулы можно уточнить, если использовать производные высших порядков.

Рассмотрим многочлен

Мне нужно представить его в виде многочлена по степеням .

Т.к. многочлен задан, то его коэффициенты известны. Выразим через этот многочлен коэффициенты

Мы получили искомое разложение многочлена по степеням .

Если заменить многочлен 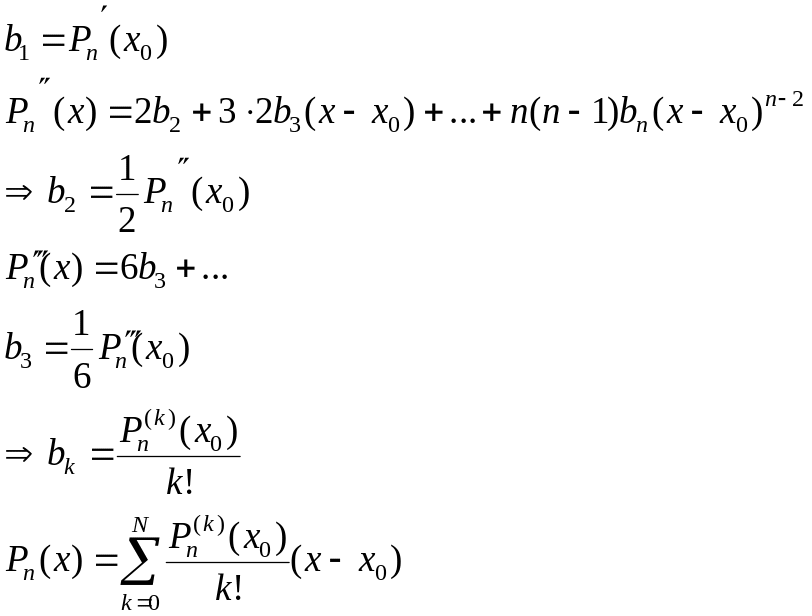на (n+1) раз дифференцируемую функцию f(x), то формула уже не будет справедливой.

Возникнет некоторая невязка , называемая остаточным членом, т.е. мы получим

(5) Докажем, что порядок малости выше, чем порядок малости любого из членов формулы (5) при , т.е. быстрее, чем любой из членов формулы (5)

Воспользуемся для этого теоремой Лопиталля:

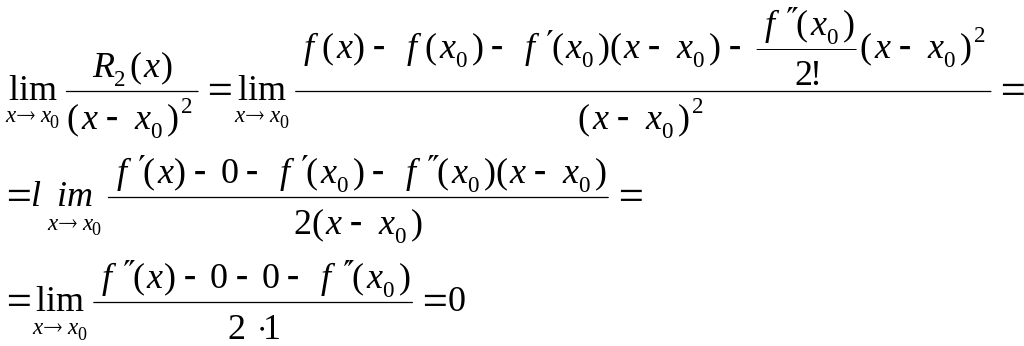Что и требовалось доказать.

Можно доказать, что имеет вид

, где и поэтому

Формула Тейлора примет вид

(6)

.

При n=0 формула (6) превращается в теорему Лагранжа, а именно

Формулу (6) можно записать в виде

(7) , здесь -многочлен Тейлора, который совпадает с функцией f(x) в точке x₀, кроме этого совпадают все их производные до этого порядка включительно. Этот многочлен дает наилучшее приближение к функции f(x) в классе многочленов.

Формулу Тейлора можно записать также с помощью дифференциалов приращений, а именно, обозначим

, тогда

65.Доказать теорему Лопиталя о раскрытии неопределенностей типа .

Пусть функции f(x) и g(x) являются бесконечно малыми при ,

т.е. и на интервале [x₀;x] удовлетворяют условиям теоремы Коши. Тогда, если

Доказательство

. Применим теорему Коши,

Устремим x к x₀, т.е. ;

Замечания.

1. Если сделать замену 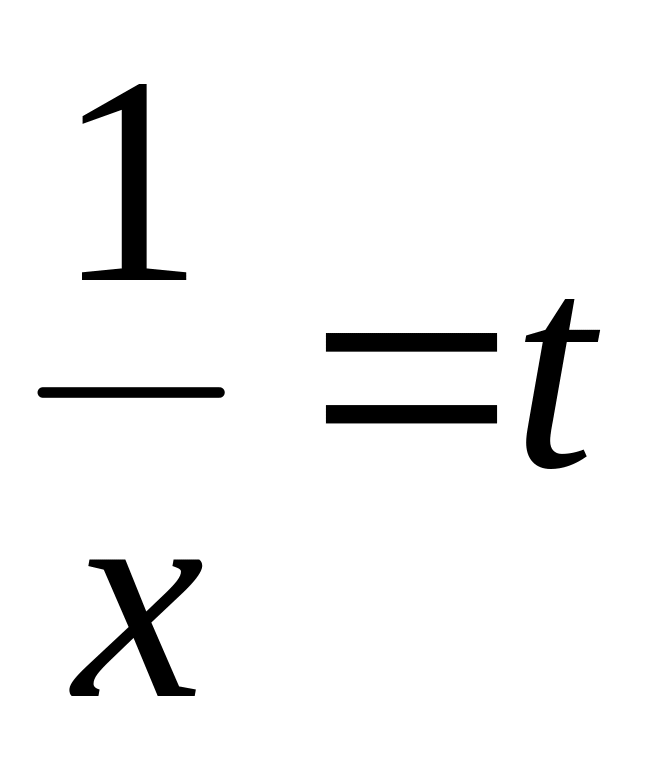, то , то

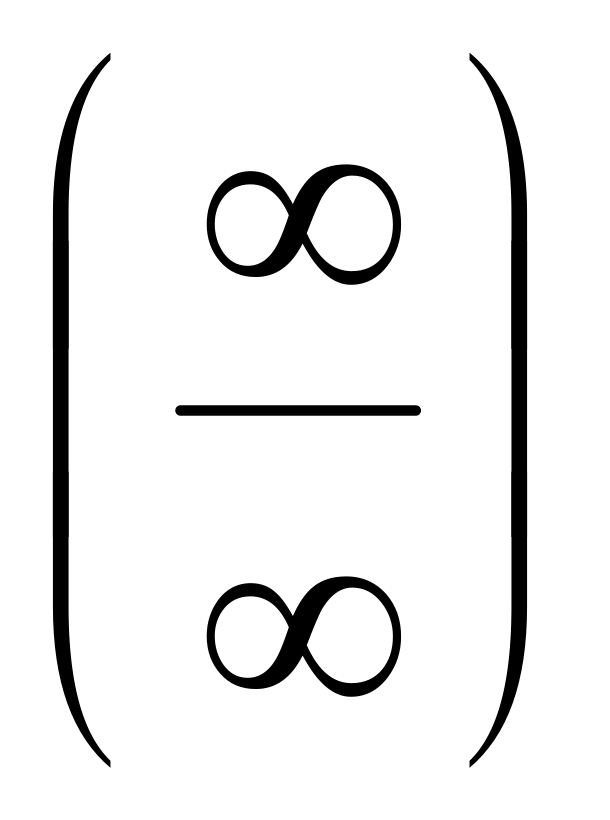
2. Теорема Лопиталя применяется неоднократно, т.е. до тех пор, пока не будет неопределенности.

3. Правило Лопиталя обычно применяется явочным порядком, т.е. не проверяются условия существования пределов, а ищется предел отношения производных. Если предел отношения каких-то производных существует, то правило Лопиталя можно применять

4. Правило Лопиталя часто бывает удобно сочетать с другими способами раскрытия неопределнности.

66. Доказать дифференциальные признаки возрастания и убывания функции.

Теорема 1.

Пусть функция y=f(x) дифференцируема в окрестности точки x₀ и в этой окрестности, тогда функция в точке

Доказательство:

По условию теоремы

и он больше 0, отсюда по теореме о связи последовательностей, имеющей предел бесконечно малый имеет

, где

Что и требовалось доказать.

Аналогично, если

Из этой теоремы следует способ нахождения интервалов возрастания и убывания функции, так называемый метод интервалов, т.е. находим производную функции, приравниваем ее к нулю, мы получаем разбиение области определения функции на ряд интервалов, в каждом из которых функция или возрастает или убывает. Направление монотонности может изменяться только при переходе через границу интервала.

Теорема 2. Если x₀- точка локального экстремума функции f(x), то или или не существует.

Доказательство вытекает из теоремы Ферма.

Эта теорема дает лишь необходимое условие экстремума.

Пусть функция f(x) дифференцируема в полной или выколотой окрестности точки x₀ и при переходе через точку x₀ производная меняет свой знак.

Если знак меняется с «+» на «-«, то x₀ – точка максимума.

Если знак меняется с»-« на «+», то x₀ – точка минимума.

Докажем, что x₀ – точка максимума.

Обозначим . По теореме Лагранжа

1. Пусть

2. Пусть

Мы получили, что

т.е.

67. Определение экстремума функции. Доказать теоремы о достаточных условиях экстремума функции.

Достаточное условие экстремума функции с помощью второй производной.

Пусть функция y=f(x) дважды дифференцируема в окрестности точки x₀ и т.е. x₀ – стационарная точка, тогда если , то x₀ – точка минимума, а если , то x₀ – точка максимума.

Доказательство.

По определению вторая производная это производная от первой производной

по теореме 1 (билет 66) точка минимума.

Теорема 1.

Пусть функция y=f(x) дифференцируема в окрестности точки x₀ и в этой окрестности, тогда функция в точке

68. Дать определение выпуклости и вогнутости. Точки перегиба.

Знание первой производной позволяет установить направление роста функции и точки ее экстремумов. Для определения более тонких характеристик, а именно выпуклости и вогнутости графика потребуется значение 2-ой производной.

Говорят, что график функции выпуклый в окрестности точки x₀ , если для любых точек x₁,x₂ из этой окрестности

Вогнутость

Теорема. Если вторая производная в точке то график функции выпуклый в окрестности точки x₀.

Доказательство.

Рассмотрим число и докажем, что оно будет больше нуля.

Воспользуемся теоремой Лагранжа:

в каждой из двух квадратных скобок.

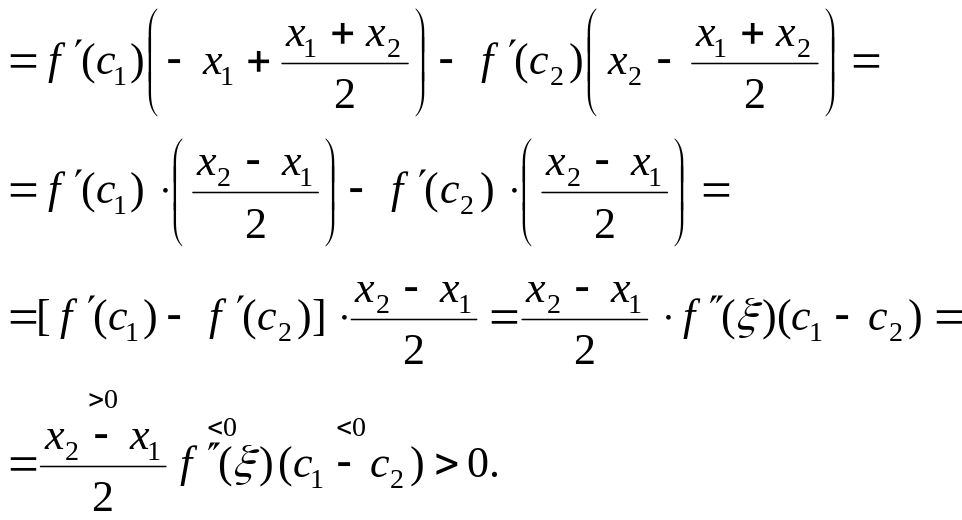
Что и требовалось доказать.

Точки, в которых выпуклость графика сменяется вогнутостью или наоборот называются точками перегиба.

Теорема.

Если и слева и справа от точки имеет разные знаки, то x₀ – точка перегиба графика функции.

69.Дать определение вертикальных и наклонных асимптот графиков функций и рассказать об их нахождении. Наименьшее и наибольшее значения функции на интервале.

Асимптотой называется прямая, к которой график функции неограниченно приближается, но не сливается с ней.

Асимптоты делятся на вертикальные и наклонные

Прямая является вертикальной асимптотой графика функции, если 1) x₀ – точка разрыва 2-ого рода; 2)

Прямая y=kx+b называется наклонной асимптотой графика функции f(x), если при расстояние между графиком функции и этой прямой неограниченно уменьшается.

Расстояние измеряется по перпендикуляру к асимптоте, однако нам удобно рассматривать вертикальные отрезки, равные

Понятно, что они тоже стремятся к нулю.

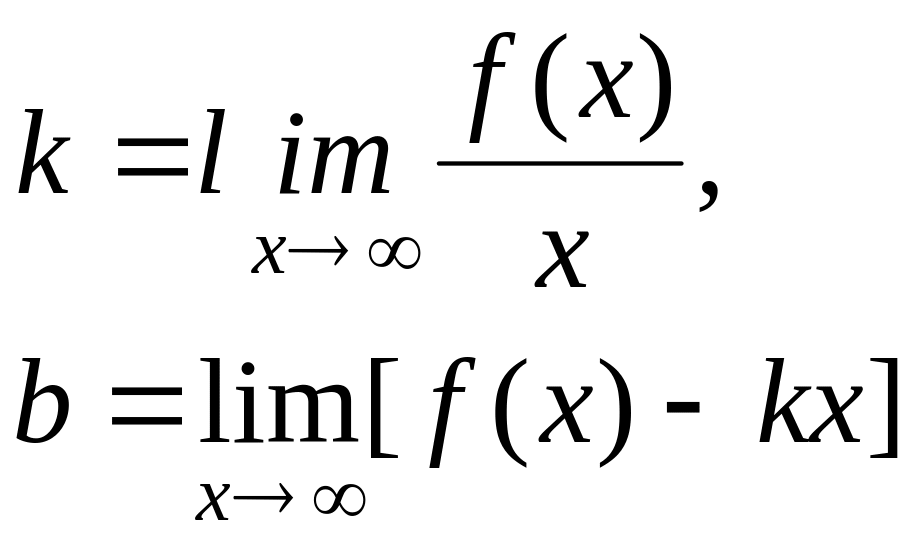
Если хотя бы один из указанных пределов не существует или равен бесконечности, то график функции не имеет наклонных асимптот.

Наибольшее и наименьшее значения функции на интервале.

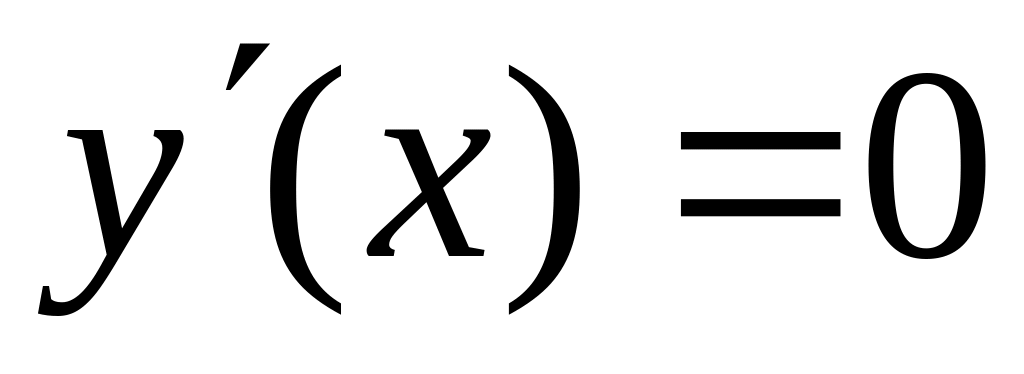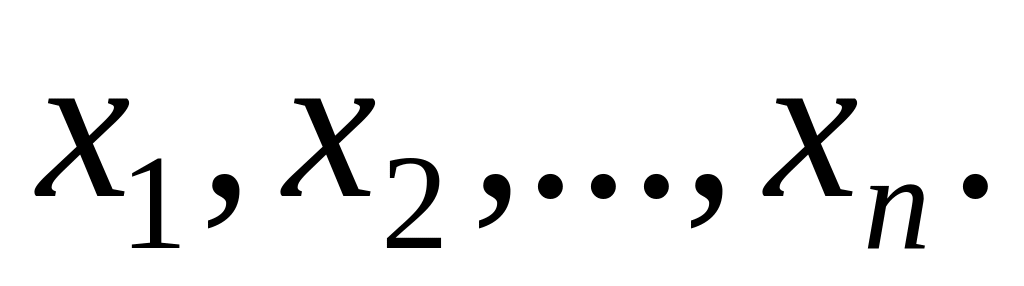1. Вычисляем и находим критические точки, т.е. те точки, где производная равна 0 или не существует. Пусть это будут точки 2) Из этих точек выбираем те, которые входят в интервал (a;b):

3)Вычисляем значения функции во всех этих точках и на концах интервала.

Наименьшее из этих чисел будет наименьшим значением функции на интервале, наибольшее – наибольшим.