8. Теорема о ранге матрицы. Решение однородных систем уравнений. Фундаментальная система решений. Примеры.

Рангом матрицы r(A) называется наивысший порядок отличного от нуля минора этой матрицы.

Тот минор, на котором реализуется ранг матрицы, называется ранговым или базисным. Он определяется неоднозначно. Очевидно. Что ранг матрицы А r(A)<=min (m,n)

Искать ранг, исходя из определения, трудно, поэтому для поиска ранга используется метод элементарных преобразований матриц. Это: 1)умножение ряда на ненулевое число; 2)сложение параллельных рядов.

Справедлива теорема:

При элементарных преобразованиях ранг матрицы не изменяется. Матрицы, полученные одна из другой элементарными преобразованиями. Называются подобными.

Из этой теоремы вытекает способ нахождения ранга матрицы:

С помощью элементарных преобразований мы добиваемся, чтобы в каждом ряде было не более одного ненулевого элемента. Количество этих элементов равно рангу матрицы.

Ранг матрицы можно искать методом окаймляющего минора.

Теорема об окаймляющем миноре.

Строки истолбцы, входящие в базисный минор, линейно не зависимы, т.е. все остальные ряды матриц являются линейными комбинациями, входящие в базисный минор. В качестве применения этой теоремы будут изучены однородные системы уравнений. Фундаментальной системой решений называют решение, через которые линейным образом выражаются все остальные. Рассмотрим однородную систему уравнений АX=0. Пусть система содержит n-неизвестных, а ее ранг равен r(A)=r, тогда (n-r) переменных объявляются свободными. Эти свободные переменные входят в линейное пространство, элементами которого являются их линейные комбинации. Это и будут все решения однородной системы, они образуют базис. Чтобы получить канонический базис, свободные переменные последовательно придаются значения…

8. Дать определение размерности и базиса линейного пространства. Разложение вектора по базису. Координаты вектора. Канонический базис. Примеры.

Будем называть алгебраическим вектором или n-мерным вектором упорядоченный набор n-чисел, т.е. вектор-строку или вектор-столбец.

Совокупность n-мерных векторов, в которой введены понятия сложения и умножения на число, удовлетворяющее некоторым очевидным свойствам, называется линейным векторным пространством Rⁿ.

Ни один из них не выражается через остальные.

Максимальное количество этих векторов называется размерностью пространства, а эти вектора – базис пространства.

8. Дать определение скаляра, вектора. Рассказать о линейных операциях над векторами и привести их основные свойства. Примеры.

8. Проекция вектора на ось. Координаты вектора. Орт вектора. Коллинеарные и компланарные векторы. Разложение вектора по базису. Примеры.

Ортом вектора а называется вектор а⁰, коллинеарный и сонаправленный вектору а, модуль которого равен 1.

12.Дать определение скалярного произведения векторов. Рассказать об его физическом смысле и основных свойствах. Вывести выражение скалярного произведения через координаты векторов. Примеры.

Скалярным произведением векторов а и b называется скаляр, равный произведению модуля этих векторов на косинус угла между ними.

Физически скалярное произведение – это работа силы

13. Дать определение модуля вектора, орта вектора и направляющих косинусов. Вывести формулы для их вычисления. Вывести формулу для вычисления угла между векторами и условие ортогональности векторов. Примеры.

Выражение координат ортовекторов, направляющие косинусы.

; ;

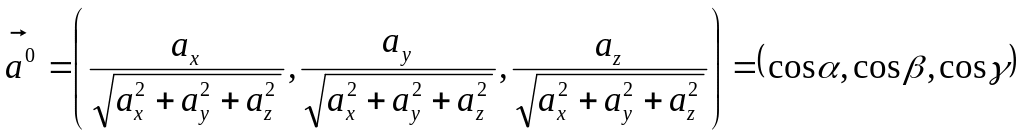
- это углы, которые составляет вектор с осями координат.

Условие ортогональности ( взаимно - перпендикулярности).

Расстояние между двумя точками.