Дать определение параболы и вывести ее каноническое уравнение. Провести исследование формы параболы по ее каноническому уравнению. Примеры.
Парабола – это множество точек плоскости, равноудаленных от точки, называемой фокусом и прямой, называемой директрисой.
Для вывода канонического уравнения параболы проведем ось OX через фокус, перпендикулярный директрисе.
А начало координат выберем посередине между ними.
Расстояние от плоскости до директрисы называется фокальным параметром.
Исследование формы параболы по ее каноническому уравнению.
Парабола проходит через начало координат.
X.>=0,т.к. p>0, y в квадрате >0.
Т.к. y входит только в квадрате, то парабола симметрична относительно оси OX.
Эллипс, гипербола, парабола как конические сечения. Общее определение кривых 2-го порядка.
Кривой второго порядка называется множество точек плоскости, для которых отношение расстояний от точки до фокуса и от точки до биссектрисы постоянно и равняется эпсилон.
Если эпсилон <1 то кривая называется эллипсом.
Если эпсилон >1 то кривая называется гиперболой.
Если эпсилон=1 то кривая называется параболой.
Конические сечения.
Рассмотрим двухполосной конус.
Конусом называется фигура, полученная движением прямой, одна точка которой проходит через фиксированную точку, называемую вершиной конуса, а другая точка расположена на фиксированной линии, называемой направляющей конуса.
Прямые образующие конус называются его образующими.
Конусы обычно называются по названию направляющей.
Замечание. Вершина конуса не лежит в плоскости направляющей.
Все кривые второго порядка могут быть получены сечением конуса некоторыми плоскостями.
Если секущая плоскость перпендикулярна оси конуса, тогда мы получаем в сечении окружность.
Если секущая плоскость проходит только через одну полость и не параллельна образующей, то в сечении получается эллипс.
Если секущая плоскость параллельна образующей, то в сечении получается парабола.
Если секущая плоскость проходит параллельно оси конуса, то в сечении получается две ветки гиперболы.
Если секущая плоскость проходит через ось конуса, то в сечении получается две пересекающиеся прямые (вырожденный случай).
Линейные отображения и их матриц. Линейное отображение плоскости на плоскость.
Отображение плоскости на плоскости.
Два множества точек плоскости U,V
Пусть заданы U,V, каждой точке U соответствует точка V.
Это и есть преобразование (отображение) плоскости в плоскость.
Преобразование называется линейным, если функции f1 и f2- линейные.
Геометрически определитель матрицы преобразования – это коэффициент изменения площади при переходе в других координатах.
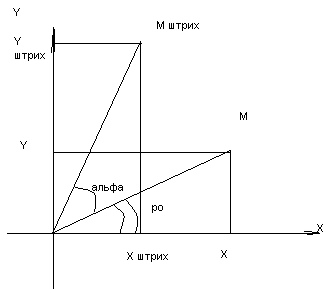
Примеры неособых линейных преобразований (растяжение. Симметрия, поворот).
Поворот.
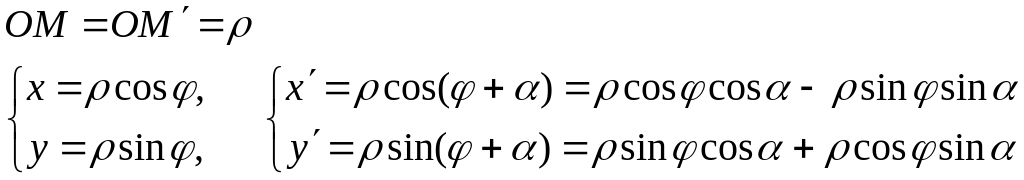
Симметричные и диагональные матрицы. Собственные векторы и собственные значения линейного отображения. Нахождение собственных значений и собственных векторов для преобразований поворота и растяжения.
Задачу о нахождении базиса, в котором матрица линейного преобразования имеет простейший вид, мы будем решать в классе симметричных матриц.
Простейшими среди симметричных матриц являются диагональные матрицы.
Рассмотрим кА диагональная матрица преобразует координатные орты.
Таким образом диагональная матрица растягивает орты и коэффициент растяжения – элементы главной диагонали.
Отсюда следует, что для приведения симметричной матрицы к простейшим (диагональному виду) нужно в качестве базиса выбрать вектор, который этой матрице растягиваются, тогда в этом новом базисе симметричная матрица превратится в диагональную.
Собственным вектором матрицы А называется ненулевой вектор b, такой что Аb=лямбда)*b,bне равен нулевому вектору.
Иначе говоря b называется собственным вектором линейного преобразования, задаваемого матрицей А.
Число лямбда называется собственным значением, соотв. Этому собственному вектору.
Не всякое линейное преобразование имеет собственный вектор. Например преобразование растяжения: всякий вектор является собственным, а в преобразовании поворота если угол не равен 0 и не равен пи, нет собственных векторов.