Дать определение обратной матрицы и доказать теорему об ее вычислении. Примеры.
Для матриц понятие делений не существует. Некоторым аналогом этого понятия являются понятие обратной матрицы.
Квадратная матрица А-1 называется обратной по отношению к квадратной матрице А, если выполняется соотношение А-1*А=А*А-1=Е; Е единичная матрица =1
Справедлива следующая теорема:У всякой не особой квадратной матрицы существует единственная обратная.Она находится по следующему алгоритму.
Находим определитель |А|≠0
Транспонируем матрицу А: АТ.
Находим присоединенную матрицу А^ =||Аij||
Она состоит из алгебраических дополнений транспонированной матрицы.
А-1=(1/|А|)*А^
Доказательство:
Докажем что для таким образом построенной матрицы выполнено соотношение А-1*А=А*А-1=Е
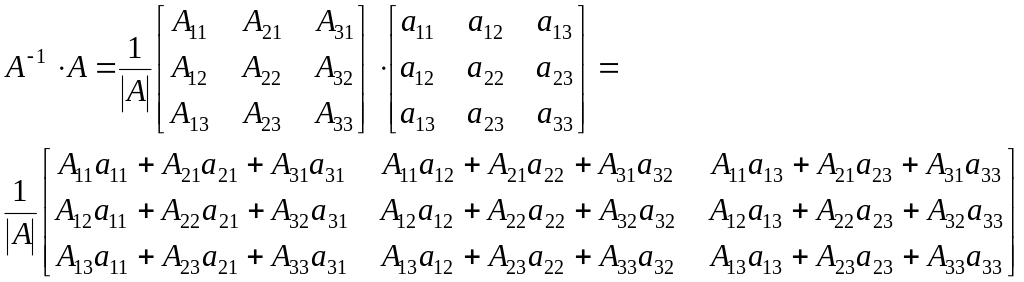
т.к.
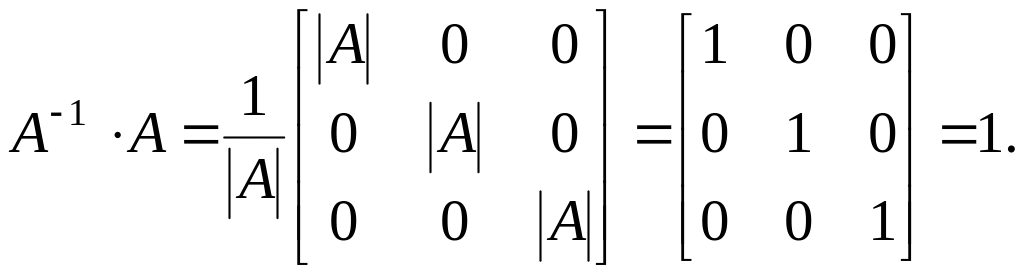
Рассказать о решении систем линейных уравнений методом обратной матрицы, по формулам Крамера и методом Гаусса. Примеры.
Формулы Крамера.
Квадратная система линейных уравнений называется Крамеровской, если ее определитель отличен от нуля.
Крамеровская система всегда имеет единственное решение, которое находится по формулам
Xk=(∆k/∆); (к принадлежит N)
Здесь ∆к – это определитель, получаемый из ∆ путем замены к-столбца на столбец свободных членов.
Замечание: Из теоремы Крамера следует, что однородная крамеровская система имеет только тривиальное решение Xk=0( k принадлежит N )
Метод Гаусса. Решение систем линейных уравнений.
Наиболее удобным методом решения прямоугольных систем уравнений является метод Гаусса ( метод последовательного исключения)
Расширенной матрицей системы называется матрица системы с присоединенным к ней столбцом правых частей. А¯ =(А/В)
Суть метода: с помощью элементарных преобразований, проводимых над строками расширенной матрицы мы приводим ее к треугольной или трапецивидной форме, а затем «обратным ходом» последовательно находим неизвестные.
Выбираем в некоторой строке в матрице А¯ направляющий элемент, обычно это ±1, и называем строку направляющей. Умножая эту строку на какие-то числа и складывая с другими строками, мы добиваемся того, что все элементы этого столбца, кроме направляющего обращаются в нули. На втором шаге выбираем направляющий элемент в другой строке и другом столбце и опять делаем нули в столбце, но при этом предыдущая направляющая строка не изменяется. Так делаем до тех пор, пока у нас не останется неиспользованных столбцов и пока все строки, кроме одной, не станут направляющими. Если в результате этих преобразований появится строка вида (00…0/0), то это означает, что соответствующее уравнение является лишним и строка вычеркивается (00…0/а) а≠0, то это означает, что система не совместна, т.е. не имеет решений.
Дать определение ранга матрицы и сформулировать теорему об элементарных преобразованиях матрицы. Рассказать о нахождении ранга матрицы методом элементарных преобразований. Примеры.
Рангом матрицы r(A) называется наивысший порядок отличного от нуля минора этой матрицы.
Тот минор, на котором реализуется ранг матрицы, называется ранговым или базисным. Он определяется неоднозначно. Очевидно. Что ранг матрицы А r(A)<=min (m,n)
Искать ранг, исходя из определения, трудно, поэтому для поиска ранга используется метод элементарных преобразований матриц. Это: 1)умножение ряда на ненулевое число; 2)сложение параллельных рядов.
Справедлива теорема:
При элементарных преобразованиях ранг матрицы не изменяется. Матрицы, полученные одна из другой элементарными преобразованиями. Называются подобными.
Из этой теоремы вытекает способ нахождения ранга матрицы:
С помощью элементарных преобразований мы добиваемся, чтобы в каждом ряде было не более одного ненулевого элемента. Количество этих элементов равно рангу матрицы.
Ранг матрицы можно искать методом окаймляющего минора.
Теорема об окаймляющем миноре.
Строки истолбцы, входящие в базисный минор, линейно не зависимы, т.е. все остальные ряды матриц являются линейными комбинациями, входящие в базисный минор. В качестве применения этой теоремы будут изучены однородные системы уравнений. Фундаментальной системой решений называют решение, через которые линейным образом выражаются все остальные. Рассмотрим однородную систему уравнений АX=0. Пусть система содержит n-неизвестных, а ее ранг равен r(A)=r, тогда (n-r) переменных объявляются свободными. Эти свободные переменные входят в линейное пространство, элементами которого являются их линейные комбинации. Это и будут все решения однородной системы, они образуют базис. Чтобы получить канонический базис, свободные переменные последовательно придаются значения…
Теорема Крокенера-Капелли о совместности системы линейных уравнений. Анализ числа решений совместной неоднородной системы.
Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы А r(A)=r(A¯)
Очевидно, что r(A)<=r(A¯)
На практике не вычисляют отдельно ранги этих матриц, а просто решают систему методом Гаусса. Если матрица примет треугольный или трапецивидный вид, то ранги равны. Если при вычислении получится строка вида (00..0/0), то соответствующее ей уравнение лишнее, и его вычеркивают.
Если получится (00…0/а) а≠0, то r(A¯)>r(A) следовательно система не совместна.
Если система совместна, то возможны следующие варианты:
r(A)=n, n- число неизвестных
В этом случае выделяем базисный минор порядка n, не входящие в него строки отбрасываются и система имеет единственное решение.
2) r(A)=r<n
В этом случае система не определена, т.е. имеет бесконечно много решений. Для их нахождения поступают следующим образом: выделяют базисный минор порядка r, переменные, соответствующие столбцам, не вошедшим в этот минор, объявляются свободными и переносятся (n-r) свободных переменных в правую часть с другим знаком, затем находится решения полученной системы с точностью до свободных переменных.
3) Если система однородна, т.е. столбец В целиком состоит из нулей, то она всегад совместна. У нее будет единственное решение, если r(A)=n – единственное тривиальное решение и бесконечно много решений, если r<n.
7. Дать определение вектора и линейного пространства. Линейная зависимость и независимость вектор-столбцов.
Будем называть алгебраическим вектором или n-мерным вектором упорядоченный набор n-чисел, т.е. вектор-строку или вектор-столбец.
Совокупность n-мерных векторов, в которой введены понятия сложения и умножения на число, удовлетворяющие некоторым очевидным свойствам, называются линейным векторным пространством Rn.
Линейная зависимость и независимость векторов.
Векторы а1, а2, …ак называются линейно-независимыми, если найдется такой набор чисел bi, что соотношение
B1a1+b2a2+…+bkak=0, выполняется только тогда, когда все числа b=0.
Эти векторы а1,а2,…ак называются линейно-зависимыми, если в равенстве хотя бы одно b≠0
Линейная зависимость векторов означает, что хотя бы один из них может быть представлен, как линейная комбинация остальных.
Размерностью линейного пространства называется максимальное число линейно-независимых векторов этого пространства.
Векторы, на которых реализуется размерность, называются базисом этого пространства.
Любой вектор пространства Rn может быть представлен в виде линейной комбинации векторов базиса. Допустим а=б1е1+б2е2+б3е3
Коэффициенты этого представления называются координатами вектора, заданного в базисе.
Если не указано противное, то координаты вектора заданы в каноническом базисе.