13. Дать определение функции. Основные элементарные функции (тригонометрические и обратные тригонометрические). Графики.

Пусть заданы два множества X и Y. Функцией называется правило, которое каждому элементу x из множества X ставит в соответствие единственный элемент y из Y.

Графиком функции называется множество упорядоченных пар точек (x,f(x)).

Посмотреть графики y=sinx, y=cosx, y=tgx, y=ctgx, y=arcsinx, y=arccosx, y=arctgx, y=arcctgx.

13. Дать определение последовательности и ее предела. Рассказать о геометрической интерпретации понятия «предел последовательности».

Последовательность – функция натурального аргумента, т.е. X=f(n) .

Пример.

1. {1,4,9,…,n²,…}={n²}

2. {1,1/2,1/3,…,1/n,…}={1/n}

3. {1,-1,1,-1,…}={(-1)ⁿ⁺¹}

4. {1,1,…}={1}

5. {0,2/2,0,2/4,…}=

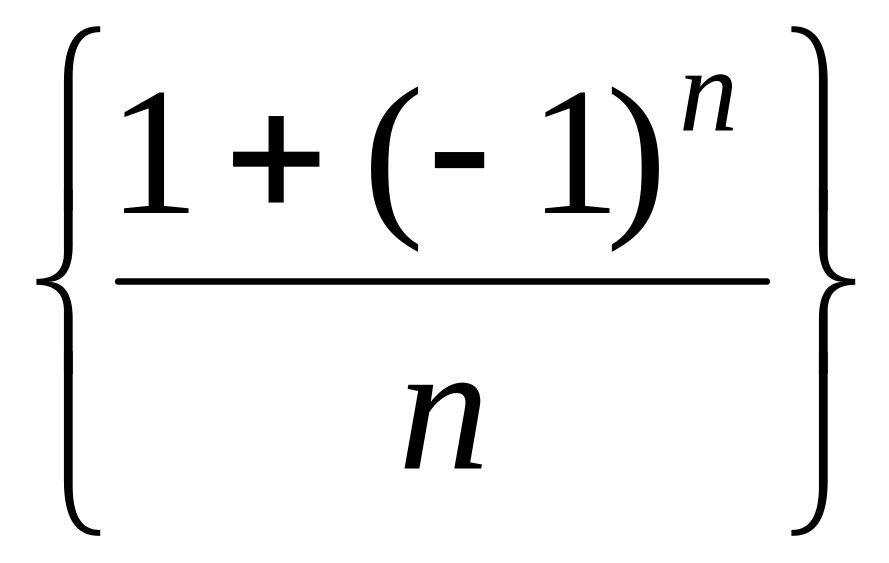
6. {1,-1/2,1/3,…}=

Последовательность называется возрастающей

и убывающей, если . Это монотонные последовательности.

Последовательность называется ограниченной сверху , ограниченной снизу , и просто ограниченной

.

Число a называется пределом последовательности x_n, если для всякого найдется номер N, зависящий от , что для всех n>N выполняется

Геометрический смысл понятия «предел последовательности».

окрестностью точки а называется интервал .

Если последовательность имеет предел, то этот предел является точкой сгущения данной последовательности, иначе говоря в окрестности этого предела находится бесконечное число членов последовательности, а вне -окрестности находится лишь конечное число не более N.

Отсюда вытекает, что добавление или отбрасывание конечного числа членов последовательности не влияет на значение ее предела.

является мерой разности между членами последовательности её предела.

Последовательность называется бесконечно-малой.

Основное различие между последовательностью и постоянной величиной состоит в том, что последовательность представляет собой некоторый процесс.

40.Дать определение бесконечно-малой и бесконечно-большой величин и доказать их основные свойства. Примеры.

Последовательность называется бесконечно-малой.

Последовательность называется бесконечно-большой.

Основные теоремы о БМ и ББ величинах.

Теорема 1. Сумма, разность и произведение конечного числа, бесконечно-малых величин, является бесконечно-малой.

Выбираем

Т.к.

Т.к.

N=max(N₁,N₂)

Теорема 2.

Теорема 3.

Последовательность, обратная к бесконечно-малой, является бесконечно-большой и соответственно наоборот.

Докажем, что

41.Дать определение бесконечно-малой бесконечно-большой величин. Примеры. Доказать теорему о связи сходящейся последовательности с бесконечно-малой.

Основные теоремы о пределах.

Теорема 1. Сходящаяся последовательность не может иметь двух различных пределов.

Т.к. а предел, то вне окрестности точки а находится конечное число членов последовательности, что противоречит тому, что b-предел.

Теорема 2. Если предел последовательности и то почти все члены последовательности меньше b.

Это означает, что все, за исключением конечного числа.

Следствие.

Сходящаяся последовательность ограничена.

Теорема 3. Предел суммы, разности и произведения последовательностей, имеющих предел, равен сумме, разности и произведению этих пределов.

Теорема 4. Предел отношения сходящейся последовательности равен отношению их пределов, если предел знаменателя не равен нулю.

Теорема 5. О пределе промежуточной переменной или теорема о 2-х милиционерах.

Пусть заданы 3 последовательности, почти все члены которых связаны соотношением и тогда

Теорема 6.

При переходе к пределу вне равенства строгий знак неравенства может смениться на нестрогий, т.е. если x_n<y_n, то .

Теорема 7. О пределе монотонной последовательности.

Если последовательность монотонно возрастает и ограничена сверху x_n<M, то она имеет предел и этот предел .

Если последовательность монотонно убывает и ограничена снизу x_n>m, то она имеет предел

42. Доказать основные теоремы о пределах (об единственности предела, о пределе суммы, произведения, частного). Примеры.

43. Доказать теорему о пределе промежуточной переменной. Сформулировать теоремы о переходе к пределу в неравенствах и о пределе монотонной переменной.

Пусть заданы 3 последовательности, почти все члены которых связаны соотношением и тогда

Доказательство:

Пусть

При переходе к пределу вне равенства строгий знак неравенства может смениться на нестрогий, т.е. если x_n<y_n, то .

О пределе монотонной последовательности.

Если последовательность монотонно возрастает и ограничена сверху x_n<M, то она имеет предел и этот предел .

Если последовательность монотонно убывает и ограничена снизу x_n>m, то она имеет предел

44. Дать определение предела функции на языке последовательностей и на языке « ». Геометрическая интерпретация понятия «предел функции».

1-ое определение играет большую роль в теории, т.к. связывает новое понятие «предел функции» с уже известным понятием «предел последовательности».

1) Предел функции на языке последовательностей.

y=f(x), . Говорят, что предел функции

2. На языке

Число А называется , если

а) f(x) определена в окрестности точки x₀. в , за исключением быть может самой точки x₀.

б) Для всякого найдется такое

б) Для всякого найдется такое

3)

Число А называется , если для всякого найдется число , что для всех x, таких, что x>M

Замечание.

В данном случае прямая y=A является горизонтальной асимптотой.

4) Бесконечный предел.

Говорят, что , если для всякого M>0 найдется такое что для всех x, таких что

Замечание:

Это случай вертикальной асимптоты x=x₀- вертикальная асимптота.

45. Рассказать о раскрытии неопределенностей с помощью алгебраических преобразований. Примеры.

Если имеется отношение 2-х бесконечно-малых или бесконечно-больших неопределенностей, то такие соотношения называются неопределенностями.

Для раскрытия неопределенностей типа алгебраической дроби при делим числитель и знаменатель почленно на старшую степень числителя и знаменателя.

Рассмотрим неопределенностей типа ( ), где числитель и знаменатель представляет собой бесконечные многочлены.

Если старшая степень числителя выше старшей степени знаменателя, то предел отношения равен .

Если старшая степень числителя ниже старшей степени знаменателя, то предел отношения равен 0.

Если старшая степень совпадает, то предел равен отношению коэффициентов при этих степенях.

Рассмотрим неопределенность типа при , т.е. числителем и знаменателем является бесконечно малый. В этом случае нужно в числителе и знаменателе выделить аннулирующий множитель и сократить на него до перехода к пределу.

Если бесконечно-малым является многочлен, то для выделения аннулирующего множителя удобно пользоваться теоремой Безу:

Если же бесконечно-малое содержит иррациональное выражение, то удобно умножить и разделить это выражение на сопряженные.

46. Вывести первый замечательный предел и привести следствия из него. Примеры.

Доказательство:

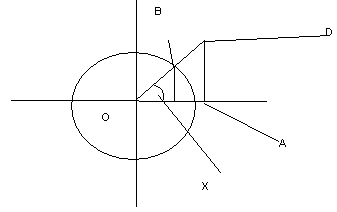
OA=1

Следствия из 1-ого замечательного предела.

1)

2)

3)

47. Вывести второй замечательный предел и привести следствия из него. Натуральные логарифмы.

Доказательство основано на формуле Бинома Ньютона

коэффициенты c, n, k можно искать с помощью треугольника Паскаля:

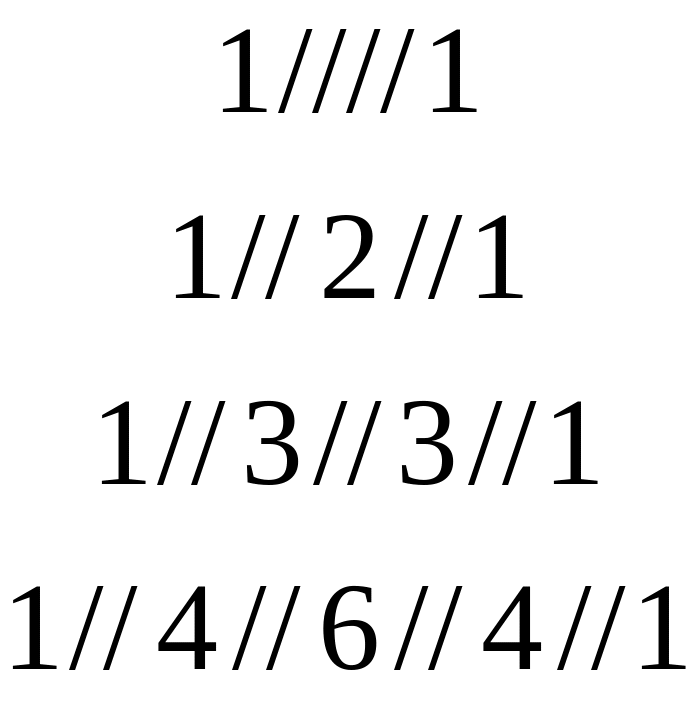
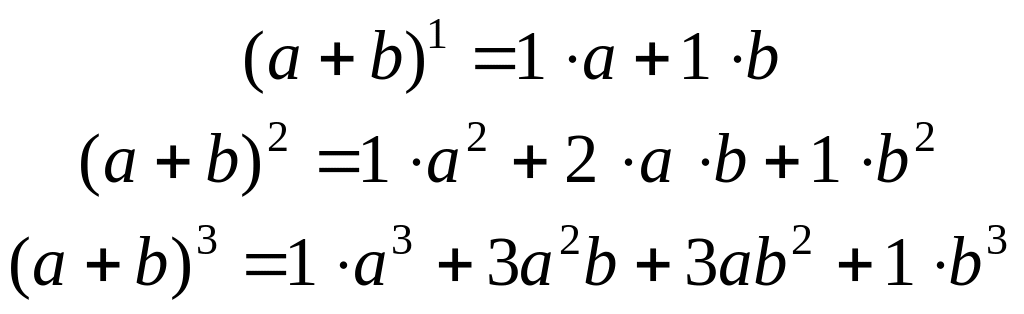
Из этого следует

1) , т.к. во-первых будет на одно слагаемое больше, а во-вторых каждый сомножитель будет больше, т.к.

2)

Доказательство:

Итак мы доказали, что и ограничена тремя, следовательно по теореме о пределе монотонно-возрастающей последовательности у нее существует предел и он меньше 3. Этот предел и называется числом e.

Т.к. любое вещественное число x может быть заключено между двумя натуральными числами n<x<n+1, то

Отсюда следует, что замечательный предел справедлив не только для последовательностей, но и для функции , т.е. может быть записан в виде

Следствия из второго замечательного предела:

1)

2)

3)

4)

5)

48. Рассказать о сравнении бесконечно-малых величин. Примеры.

Пусть - бесконечно-малые при ,т.е. , здесь x из некоторой окрестности точки x₀.

Тогда отношение является неопределенностью, типа

1. Говорят, что величина имеет высший порядок малости по отношению к 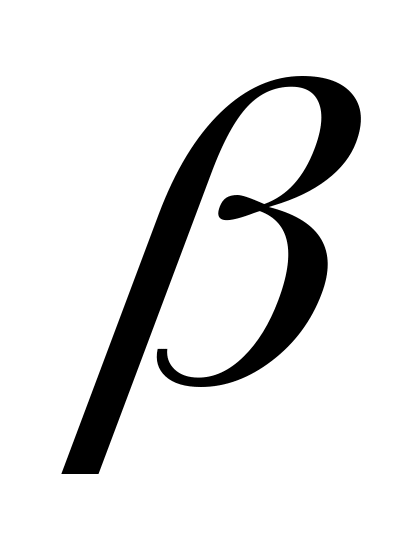: 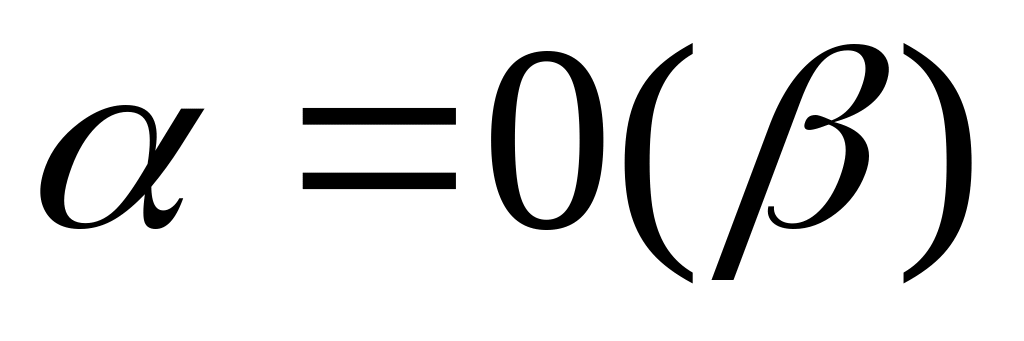, если

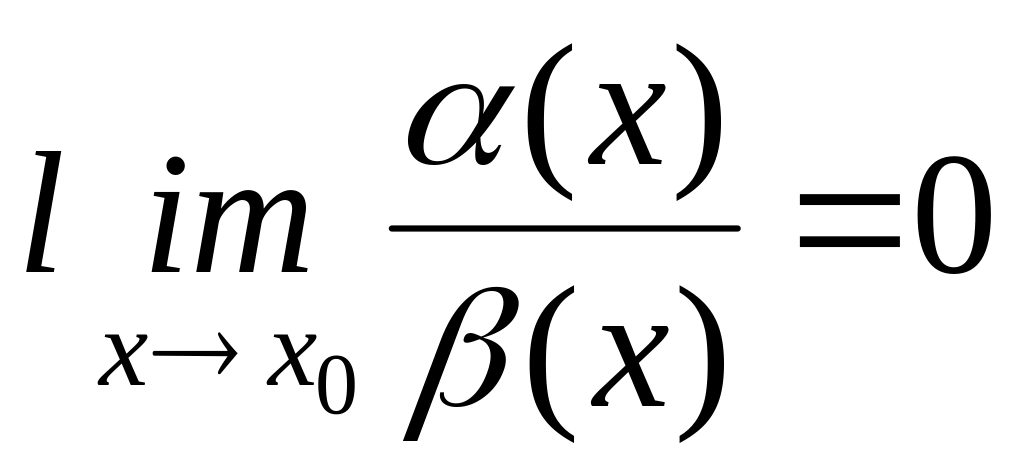
2. Говорят, что и имеют одинаковый порядок малости, если

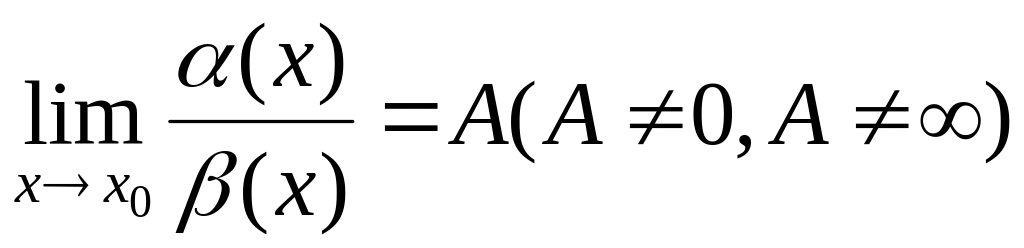
3. Величины и называются эквивалентными при , если

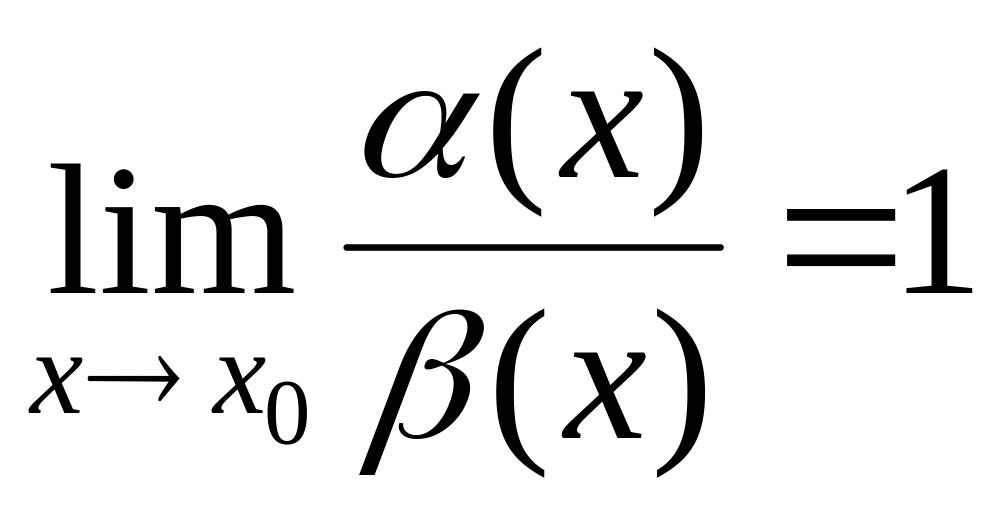
При

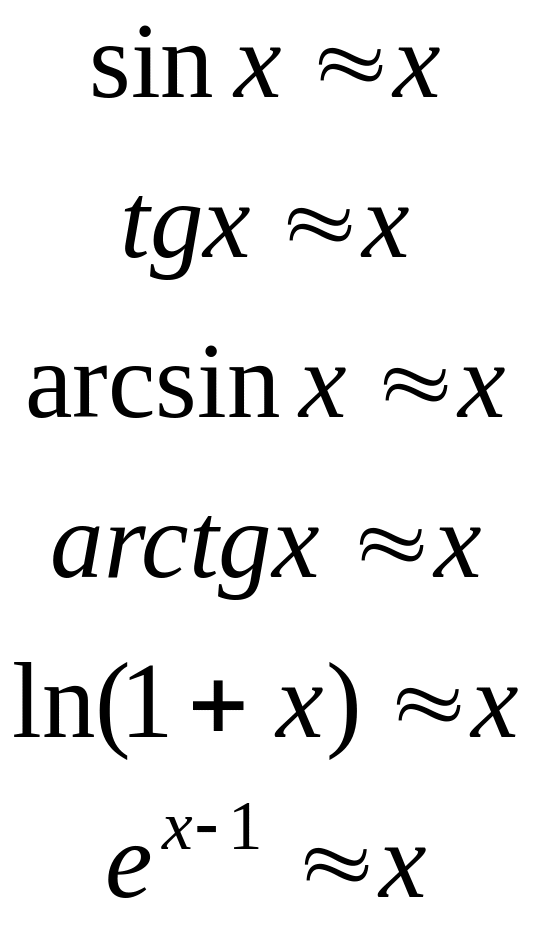
49. Дать определение эквивалентных бесконечно-малых величин. Доказать их основные свойства и рассказать об использовании этих свойств при вычислении пределов. Примеры.

1) Взаимность. Если то

2) Транзитивность. Если

3) Разностью эквивалентных бесконечно-малых являются бесконечно-малые высшего порядка по отношению к любой из них.

4. В отношениях и произведениях эквивалентные бесконечно-малые можно заменять друг на друга.

Доказательство 2):

Доказательство 3):

Доказательство 4):

50. Привести различные определения непрерывности функции в точке.

1) Пусть функция f(x) определена в окрестности точки x₀.

Определение1.

Она называется непрерывной в точке x₀, если или другими словами . Отсюда вытекает, что для непрерывной функции знак функции и предела можно менять местами.

Определение2.

На языке и для всякого найдется такое , зависящее от , что для всех

Определение 3.

Обозначим через , а через

Функция называется непрерывной в точке x=x₀, если бесконечно-малому приращению аргумента соответствует бесконечно-малое приращение функции

Определение 4. Развернутое определение непрерывности функции в точке.Функция f(x) называется непрерывной в точке x₀, если

1. f(x) определена в окрестности точки x₀.

2. Существуют односторонние пределы

и и они конечны.

3. Эти пределы равны между собой, т.е.

4) Предел функции при стремлении к предельной точке равен значению функции в этой точке.

Если хотя бы одно из этих условий не выполняется, то функция называется разрывной в точке x₀.

51. Дать определение точек разрыва и привести их классификацию. Примеры.

Функция f(x) называется непрерывной в точке x₀, если

4. f(x) определена в окрестности точки x₀.

5. Существуют односторонние пределы

и и они конечны.

6. Эти пределы равны между собой, т.е.

4) Предел функции при стремлении к предельной точке равен значению функции в этой точке.

Если хотя бы одно из этих условий не выполняется, то функция называется разрывной в точке x₀.

Классификация разрывов.

Говорят, что функция f(x) имеет в точке x₀ разрыв 1-ого рода, если оба односторонних предела существуют и конечны, но не равны между собой.

называется скачком, т.е. функция имеет конечный скачок.

Говорят, что функция f(x) имеет в точке x₀ разрыв 2-ого рода, если хотя бы один из односторонних пределов не существует или равен бесконечности.

Говорят, что функция f(x) имеет в точке x₀ устранимый разрыв, если оба односторонних предела существуют, равны между собой, но .

52. Доказать теоремы об алгебраических операциях над непрерывными в точке функциями, о непрерывности в точке суперпозиции функций и о непрерывности элементарных функций. Примеры.

Теорема 1.

Основные элементарные функции непрерывны в своей области определения.

Теорема 2.

Если функции f(x) и g(x) непрерывны в точке x₀, то непрерывными в точке x₀ являются функции [f(x)±g(x)], , , если (g(x₀)≠0).

Теорема 3.

Суперпозиция непрерывных функций является непрерывной функцией. Пусть функция y=f(x) непрерывна в точке x₀, а функция z=g(y) непрерывна в точке y₀, тогда x – суперпозиция: z=g[f(x)] непрерывна в точке x₀.

Доказательство.

Обозначим через , через и через . Воспользуемся 3 определением (Определение 3. Обозначим через , а через

Функция называется непрерывной в точке x=x₀, если бесконечно-малому приращению аргумента соответствует бесконечно-малое приращение функции

) непрерывности:

В силу непрерывности функции g(y) при .

В силу непрерывности функции f(x) при .

Итак, мы получили, что , откуда следует, что функция z=g[f(x)] непрерывна в точке x₀.

Теорема 4. Все элементарные функции непрерывны в своей области определения.

53. Сформулировать свойства функций, непрерывных на замкнутом интервале. Привести геометрическую иллюстрацию этих свойств.

Непрерывные на замкнутом интервале функции обладают рядом замечательных свойств, большинство из которых были открыты К. Вейерштрассом.

Теорема 1.

Непрерывная на замкнутом интервале функция ограничена, т.е. имеется горизонтальная полоса, в которой размещены все значения функции.

Невыполнение условий теоремы может повлечь за собой невыполнение ее утверждений.

Теорема 2.

Непрерывная на замкнутом интервале функция достигает на нем своего наименьшего и наибольшего значений. Существуют точки такие что

Теорема 3.

Непрерывная на замкнутом интервале функция вместе с любыми двумя своими значениями содержит и все промежуточные значения, т.е.

Пусть f(x₁)=A, f(x₂)=B. Тогда для существует точка , такая что .

Следствие.

Если на концах интервала (a,b) функция принимает значения разных знаков, т.е. , то найдется точка c из (a,b), такая что f(c)=0.

Это следствие является основой приближенных методов решения любых трансцедентных уравнений вида f(x)=0.

Для этого нужно сначала выделить интервал, на концах которого функция f(x) принимает значения разных знаков.

Простейшим методом приближенного нахождения решений является метод дистании.

Размер клетки – точность нахождения решения (решение ищется приближенное).

54. Дать определение производной. Рассказать об ее геометрическом и физическом смысле. Вывести уравнения касательной и нормали к плоской кривой. Примеры.

Пусть задана функция y=y(x) и пусть задан ее график и проведем через точки M₀(x_0,y₀), M(x,y), лежащие на графике этой функции, прямую, называемую секущей.

Будем теперь точку М двигать по графику к точке М₀.

Определение. Предельное положение секущей, при котором точка М совпадает с точкой М₀, называется касательной.

Если существует предел при , то он называется производной от функции y в точке x₀.

Физически производная пути по времени это мгновенная скорость, геометрически производная функция в точке x₀ является тангенсом угла наклона касательной к графику функции в этой точке.

55. Вывести формулы дифференцирования функций y=x²,y=sinx, y=cosx.

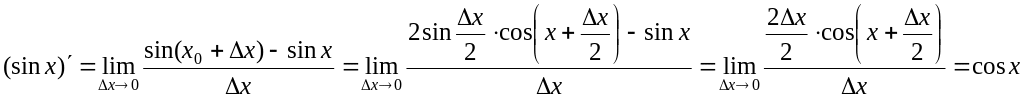
56. Дать определение дифференциала функции. Доказать теорему о связи непрерывности функции и ее дифференцируемости.

Если функция имеет производную в некоторой точке, то она дифференцируема в этой точке.

Если функция имеет производную в каждой точке некоторого множества, то она называется дифференцируемой на этом множестве.

Теорема 1.

Если функция y=y(x) дифференцируема в точке x₀, то она непрерывна в этой точке.

Доказательство:

Дифференцируемость в точке x₀ означает, что существует По теореме о связи последовательности, имеющей предел, с бесконечно-малым, т.е. по теореме

, -БМ, которая остается справедливой и для функций, имеет вид

, где

иначе

---Проанализируем это:

, а это и означает непрерывность функции в точке x₀. Теорема доказана.

, иначе дифференциал – это главное линейное приращение функции.

Геометрически дифференциал – это приращение ординаты касательной к графику функции.

, т.е. производную можно понимать как отношение дифференциалов.

57. Рассказать о связи приращения функции с ее дифференциалом и о геометрическом смысле дифференциала. Инвариантность формы 1-ого дифференциала.

Геометрически дифференциал – это приращение ординаты касательной к графику функции.

, т.е. производную можно понимать как отношение дифференциалов.

Свойство инвариантности состоит в том, что вид первого дифференциала не изменяется, если функция зависит от независимой (или промежуточной) переменных.