Вывести уравнение плоскости в отрезках на координатных осях и уравнение плоскости, проходящей через три заданные точки. Примеры.
Пусть
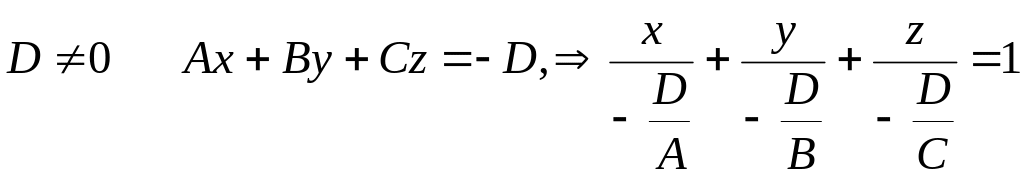
Уравнение плоскости, проходящей через три заданные точки.
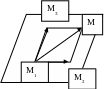
Векторы
компланарны
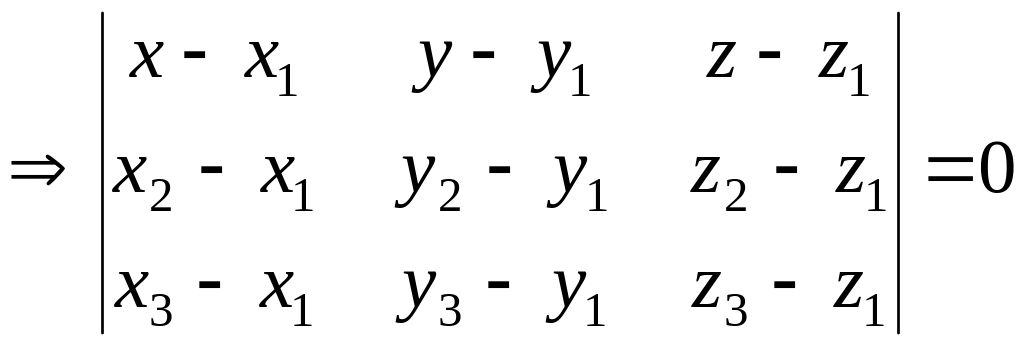
Вывести уравнение плоскости, проходящей через заданную точку и имеющую заданную нормаль. Общее уравнение плоскости и его исследования. Примеры.
,
Уравнение плоскости, проходящей через заданную точку и имеющую заданную нормаль
Частные случаи расположения плоскости:
D=0 плоскость проходит через начало координат.
A=0 плоскость параллельна оси OX
B=0 плоскость параллельна оси OY
C=0 плоскость параллельна оси OZ
A=D=0 плоскость проходит через ось OX (содержит ось OX)
A=B=0 плоскость перпендикулярна оси OZ (горизонтальная плоскость).
A=C=0 плоскость перпендикулярна оси OY
B=C=0 плоскость перпендикулярна оси OX.
A=B=D=0,CZ=0,
Z=0
плоскость
(XOY)X=0, плоскость (YOZ)
Y=0, плоскость (XOZ)
Вывести формулу для нахождения угла между двумя плоскостями и условия параллельности и перпендикулярности плоскостей. Рассказать о нахождении расстояния от точки до плоскости. Примеры.
Угол между плоскостями равен углу между их нормальными векторами.
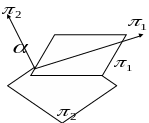
Используя формулу скалярного произведения
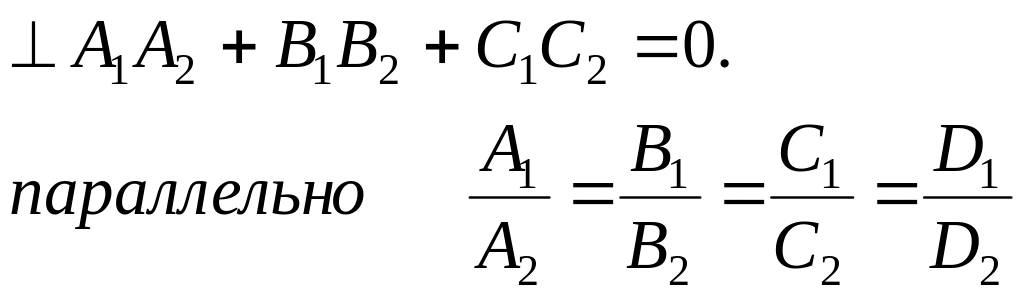
Вывести канонические и параметрические уравнения прямой в пространстве и уравнение прямой, проходящей через две заданные точки. Примеры.
Составить уравнение
прямой, проходящей через
параллельно вектору
(
уравнение прямой, проходящей через
заданную точку с заданным направляющим
вектором.(каноническое уравнение))
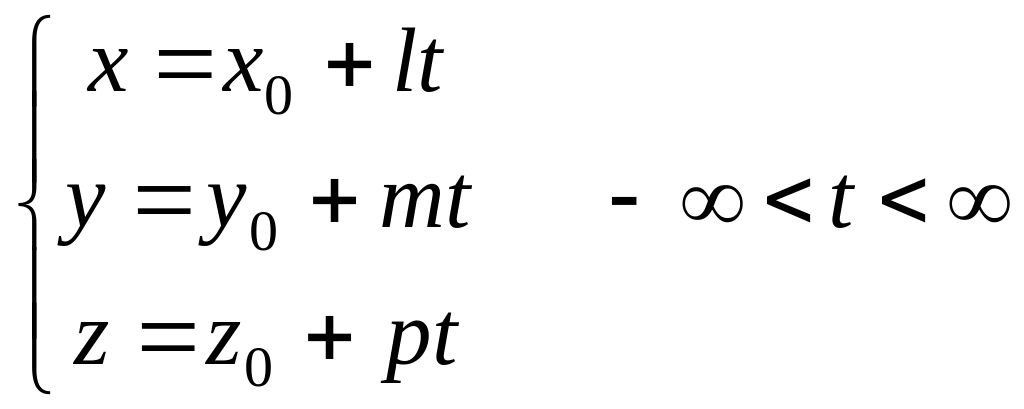
Параметрически уравнение прямой в пространстве.
Пусть заданы две точки M1 и M2.
Составим уравнение прямой, проходящей через эти две точки.
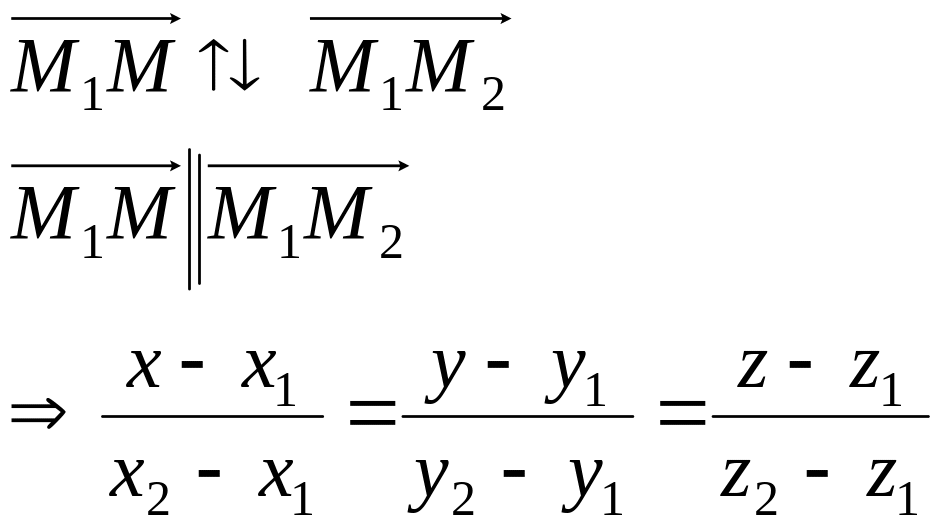
Чтобы перейти от
общих уравнений к каноническому
уравнению, нужно зафиксировать какую-то
из координат x,y
или z
и решить систему уравнений. Тем самым
мы найдем точку M0,
а вектор
Вывести формулу для нахождения угла между двумя прямыми в пространстве и условия параллельности и перпендикулярности прямых в пространстве. Примеры.
Угол между двумя прямыми, как угол между их направляющими векторами.
Рассказать о нахождении координат точки пересечения прямой и плоскости. Вывести формулу для нахождения угла между прямой и плоскостью. Примеры.
Угол между прямой и плоскостью – угол между прямой и ее проекцией на эту плоскость.
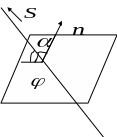
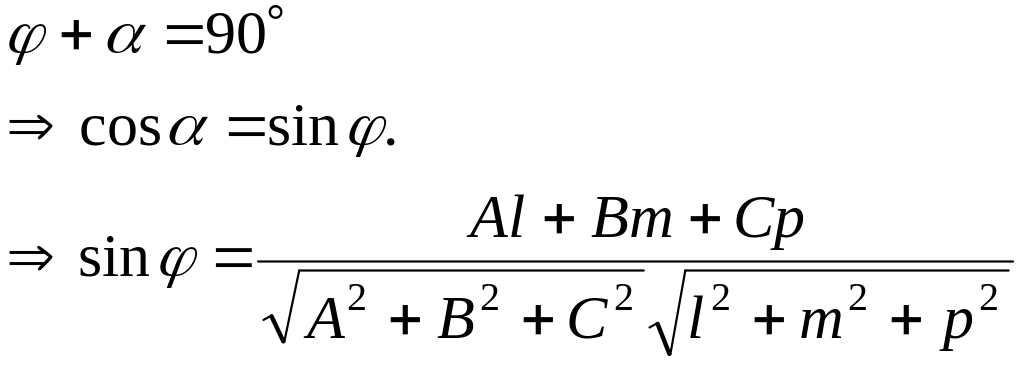
Для того, чтобы найти точку пересечения прямой и плоскости нужно в общее уравнение плоскости Ax+By+Cz+D=0 вместо текущих координат x,y,z подставить текущие координаты параметрического уравнения прямой.
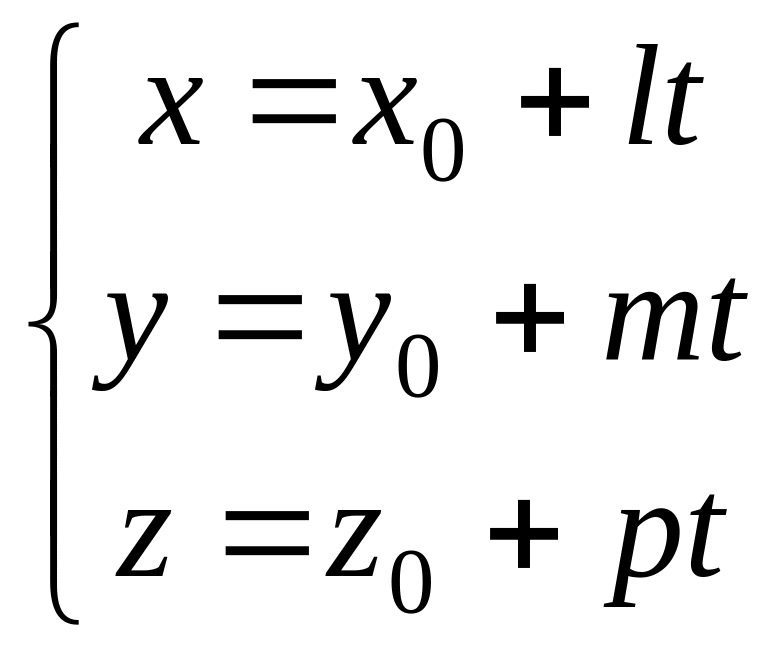
Затем решить
полученные уравнения относительно t.
Если при этом мы получим уравнение вида
,
то прямая лежит в плоскости.
Вывести уравнение прямой на плоскости, заданной угловым коэффициентом и точкой и уравнение прямой с угловым коэффициентом. Примеры.
Вывести уравнение прямой на плоскости, проходящей через две заданные точки, общее уравнение прямой на плоскости и уравнение прямой в отрезках на осях. Примеры.
Вывести формулу для нахождения угла между прямыми на плоскости и условия параллельности и перпендикулярности прямых. Рассказать о нахождении расстояния от точки до прямой. Примеры
Дать определение эллипса, записать его каноническое уравнение и провести исследование формы эллипса по его каноническому уравнению. Эксцентриситет и директрисы эллипса. Примеры.
Эллипс – это множество точек плоскости, сумма расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная.
Исследование формы эллипса по его каноническому уравнению.
Найдем точки пересечения эллипса с осями координат.
Т.к. x и y входят только в квадраты, то эллипс симметричен относительно обеих координат осей.
Эллипс может быть получен из окружности путем сжатия вдоль одной из осей.
2с – фокусное расстояние
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большой оси, характеризует степень сжатости эллипса.
Директрисами эллипса называются прямые, задаваемые уравнениями x=плюс минус (а/эпсилон), т.к. эпсилон<1 то эти прямые расположены вне эллипса
Дать определение гиперболы, записать ее каноническое уравнение и провести исследование формы гиперболы по ее каноническому уравнению. Эксцентриситет, директрисы и асимптоты гиперболы. Примеры.
Гипербола – это множество точек плоскости, разность расстояний от которых до двух фиксированных точек плоскости, есть величина постоянная.
Исследование формы гиперболы по ее каноническому уравнению.
Асимптотами гиперболы называются прямые задаваемые уравнением y= плюс минус (b/a)*x..
На практике гиперболу удобно строить следующим образом: рисуем прямоугольник со сторонами 2а, 2b с центром в начале координат, его диагонали являются асимптотами гиперболы, а точки плюс минус а – пересечение гиперболы с осью OX