
- •Пространство элементарных событий.
- •Совместные и несовместные события.
- •Операции над событиями (сумма, разность, произведение).
- •Свойства операций над событиями.
- •Алгебра и сигма-алгебра событий.
- •Классическое определение вероятности события. Случаи равновероятных исходов.
- •Статистическое определение вероятности события. Случаи неравновероятных исходов.
- •Геометрические вероятности.
- •Аксиоматическое построение теории вероятностей.
- •Полная группа событий.
- •Условная вероятность.
- •Независимость событий.
- •Основные понятия комбинаторики.
- •Правила суммы и произведения.
- •Случай непостоянной вероятности появления события в опытах
- •Для того чтобы найти вероятность появления события ровно раз в серииопытов, достаточно произвести перемножение сомножителей в производящей функции. Коэффициент при членеи даст искомую вероятность.
- •Предельные теоремы для схемы Бернулли.
- •Теорема Пуассона.
- •Понятие потока событий.
- •Локальная теорема Муавра –Лапласа.
- •Интегральная (глобальная) теорема Муавра – Лапласа.
- •Закон распределения дискретной случайной величины.
- •Свойства функции распределения
- •Свойства математического ожидания:
- •Дисперсия случайной величины и ее свойства.
- •Среднее квадратическое отклонение.
- •Распределение Пуассона.
- •Геометрическое распределение
- •Гипергеометрическое распределение (урновая схема)
- •Равномерное распределение.
- •Показательное распределение.
- •Свойства функции Гаусса.
- •Вероятность попадания нормальной случайной величины в заданный интервал.
- •Где - функция Лапласа.
- •Функция Лапласа и ее свойства.
- •Отклонение нормальной случайной величины от ее математического ожидания. Правило «трех сигм».
- •Закон распределения вероятностей двумерной случайной величины
- •Свойства совместной функции распределения двух случайных величин
- •Плотность совместного распределения вероятностей непрерывной двумерной случайной величины
- •Свойства двумерной плотности вероятности
- •Независимые случайные величины
- •Для независимых случайных величин справедливы соотношения
- •Корреляционный момент
- •Коэффициент корреляции Коэффициентом корреляции случайных величинX и y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:
- •Свойства коэффициента корреляции
- •Способы отбора На практике применяются различные способы отбора, которые можно подразделить на два вида:
- •Выборочные среднее и дисперсия
- •Статистический критерий
- •A. Понятие о корреляционном анализе
- •Линейная регрессия
- •Множественная линейная регрессия
- •Нелинейная регрессия
- •Однородные цепи Маркова
- •Понятие о системах массового обслуживания
Свойства операций над событиями.
Некоторые свойства операций над событиями постулируются, другие легко могут быть получены с помощью диаграмм Венна. Приведем без доказательства основные из этих свойств.
Алгебра и сигма-алгебра событий.
Пусть
![]() является пространством всех элементарных
исходов для какого-нибудь случайного
эксперимента, каждому результату
которого соответствует ровно одна точка
является пространством всех элементарных
исходов для какого-нибудь случайного
эксперимента, каждому результату
которого соответствует ровно одна точка![]() .
Выделим совокупность подмножеств
.
Выделим совокупность подмножеств![]() множества
множества![]() .
При этом потребуем, чтобы
.
При этом потребуем, чтобы![]() содержало как случайные события
содержало как случайные события![]() ,
так и события, полученные в результате
применения любой из описанных операций
к любым элементам системы.
,
так и события, полученные в результате
применения любой из описанных операций
к любым элементам системы.
Совокупность
![]() случайных событий
случайных событий![]() (подмножеств множества
(подмножеств множества![]() ),
определенных на пространстве элементарных
исходов
),
определенных на пространстве элементарных
исходов![]() ,
называетсяалгеброй событий (илибулевой алгеброй– по имени
английского математика Дж. Буля (1815 –
1864)), если выполнены следующие условия:
,
называетсяалгеброй событий (илибулевой алгеброй– по имени
английского математика Дж. Буля (1815 –
1864)), если выполнены следующие условия:
 ;
;Если
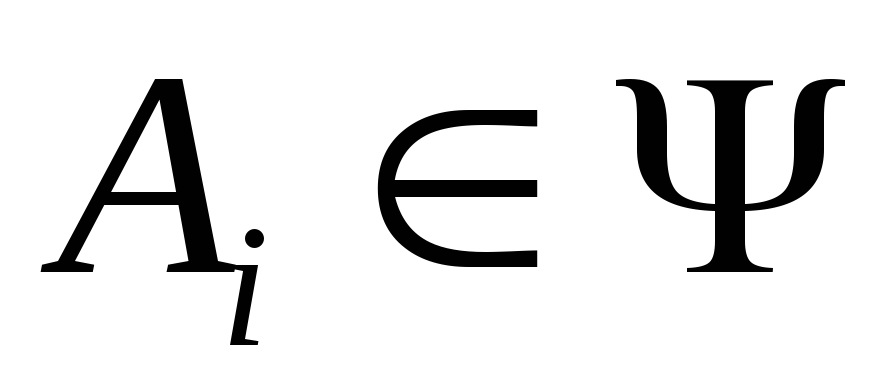 и
и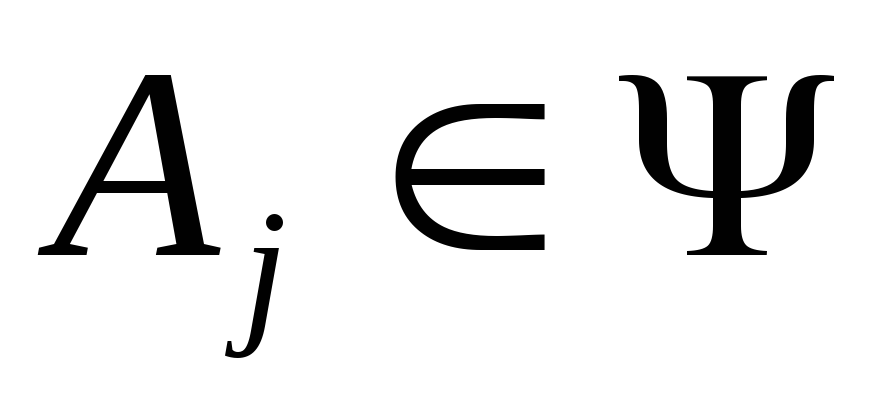 ,
то
,
то для
любых
для
любых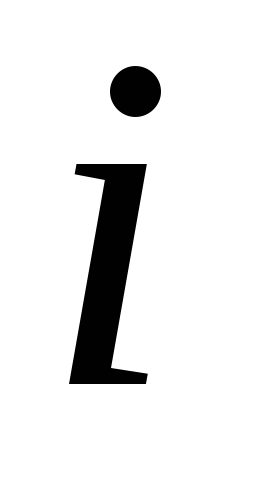 и
и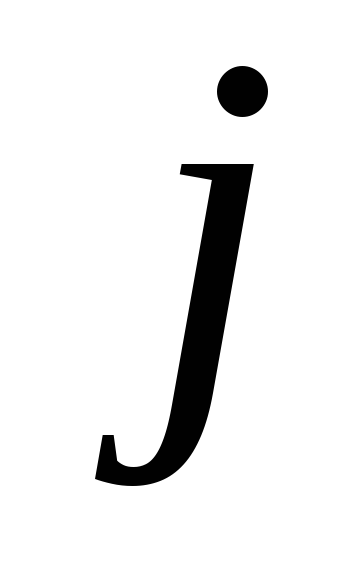 ;
;Если
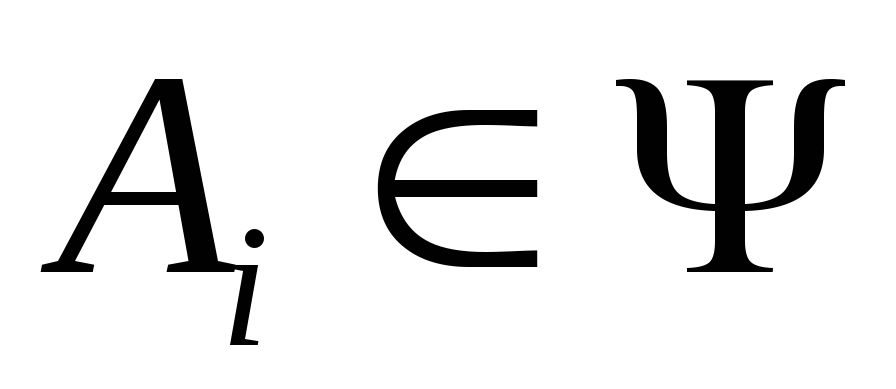 ,
то
,
то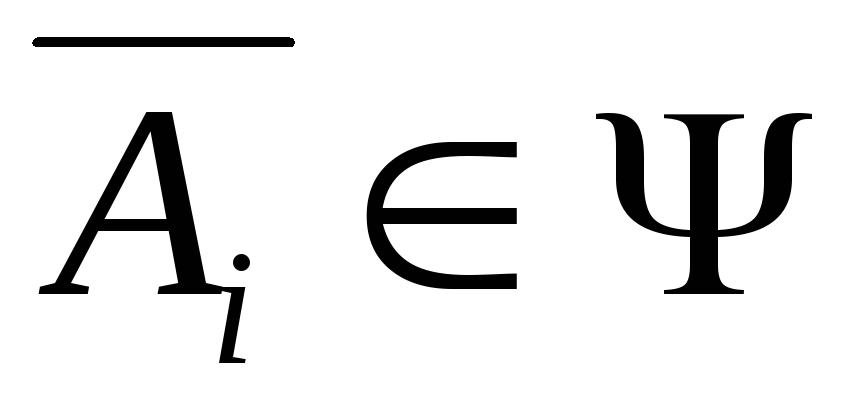 .
.
Оказывается, что
условий 1 – 3 достаточно для того, чтобы
любое конечное число других операций
над случайными событиями
![]() не выводило бы нас за пределы алгебры
не выводило бы нас за пределы алгебры![]() .
Для экспериментовс конечным числом
исходов множество всех подмножеств
.
Для экспериментовс конечным числом
исходов множество всех подмножеств![]() ,
включающее пустое множество,
составляет алгебру. Поэтому для таких
экспериментов любое подмножество
множества
,
включающее пустое множество,
составляет алгебру. Поэтому для таких
экспериментов любое подмножество
множества![]() может интерпретироваться как наблюдаемое
событие.
может интерпретироваться как наблюдаемое
событие.
Во многих задачах теории вероятностей приходится иметь дело и с бесконечным числом элементарных исходов и, следовательно, операций. Это потребовало введения понятия -алгебры событий.
Система подмножеств
![]() множества, называется-алгеброй,
если она удовлетворяет следующим
условиям:
множества, называется-алгеброй,
если она удовлетворяет следующим
условиям:
 ;
;Если
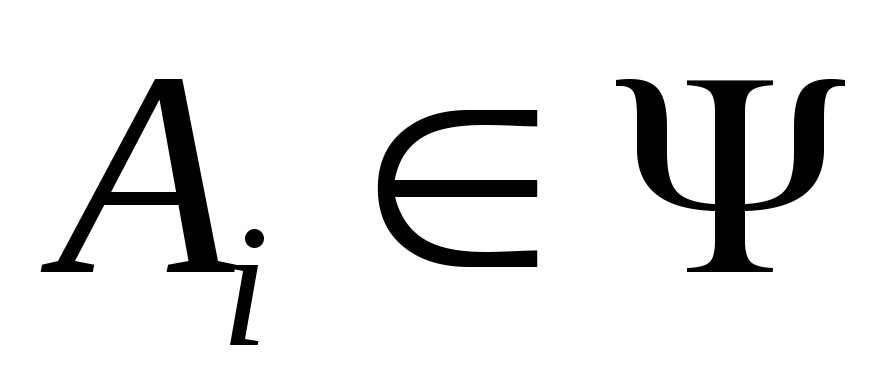 , то
, то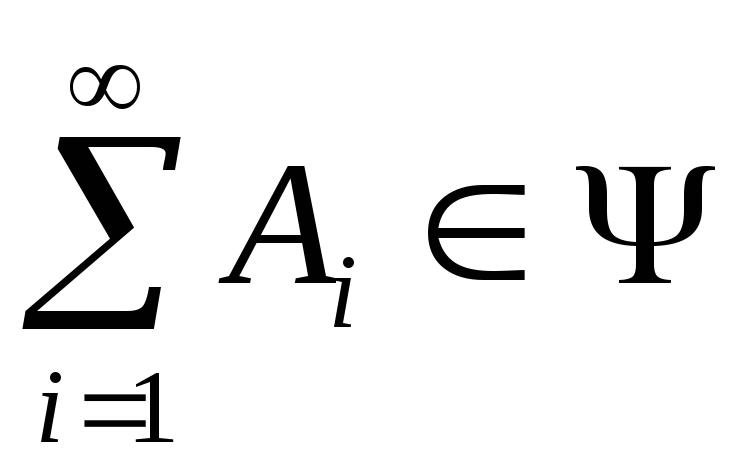 и
и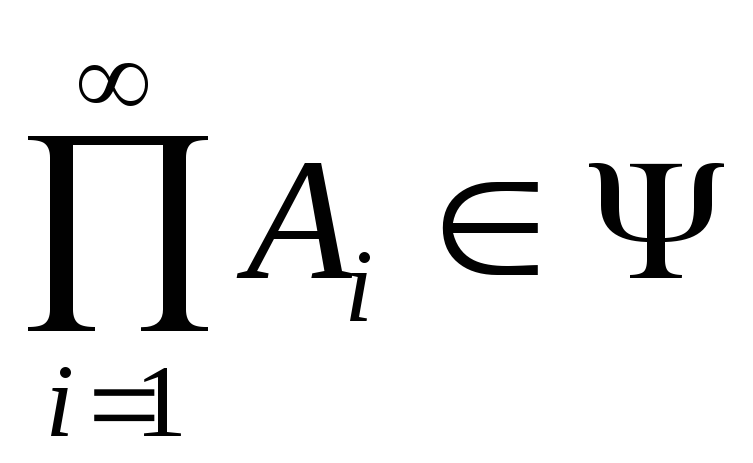
Если
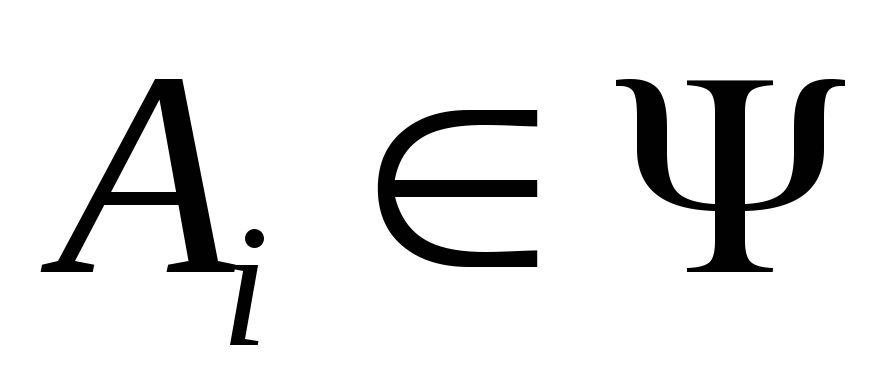 ,
то
,
то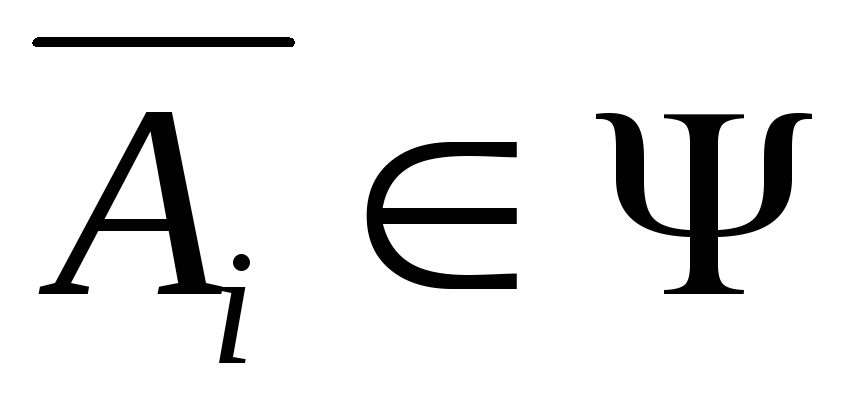 .
.
Таким образом, счетное число операций суммирования или перемножения событий не выводит результирующее событие за пределы –алгебры.
Лекция 3. Классическое определение вероятности события. Статистическое определение вероятности. Геометрические вероятности. Аксиоматическое построение теории вероятностей. Вероятностное пространство.
Вероятностьявляется количественной мерой возможности появления события. Наиболее широкое распространение получили два определения вероятности события: классическое и статистическое.
Классическое определение вероятности события. Случаи равновероятных исходов.
Классическое определение вероятностисвязано с определением благоприятствующего исхода. Исход называется благоприятствующим данному событию, если его появление влечет за собой наступление этого события.Вероятность события равна отношению числа равновозможных благоприятствующих элементарных исходов к общему числу всех равновозможных элементарных исходов данного испытания:
![]() ,
,
где ![]() –
число благоприятствующих событию
–
число благоприятствующих событию![]() исходов;
исходов;
![]() – общее число возможных исходов.
– общее число возможных исходов.
Примеры:1. Кубик, 2. Какова вероятность того, что в произвольном двузначном числе две цифры одинаковы (9/90 = 0.1), 3. Из букв слова “дифференциал” выбирается одна буква. Какова вероятность того, что это а) гласная, б) буква “ф”.
Из определения
вероятности события
![]() следует, что
следует, что![]() ,
поэтому всегда выполняются неравенства
,
поэтому всегда выполняются неравенства![]() ,
т.е.вероятность любого события есть
неотрицательное число, не превышающее
единицы.
,
т.е.вероятность любого события есть
неотрицательное число, не превышающее
единицы.
Если
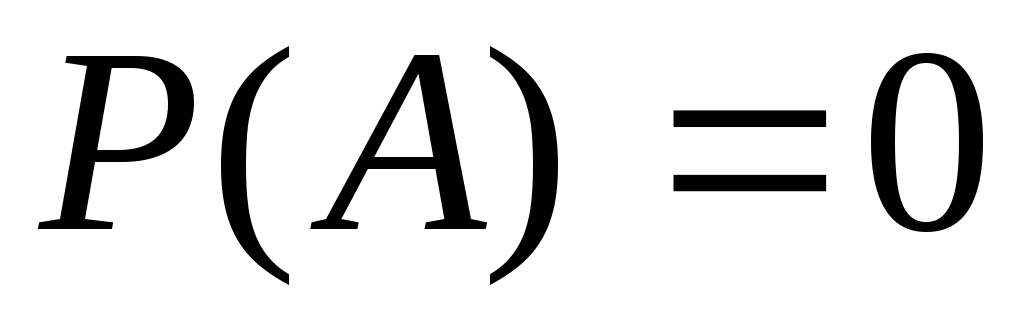 ,
то событие
,
то событие невозможное.
невозможное.Если
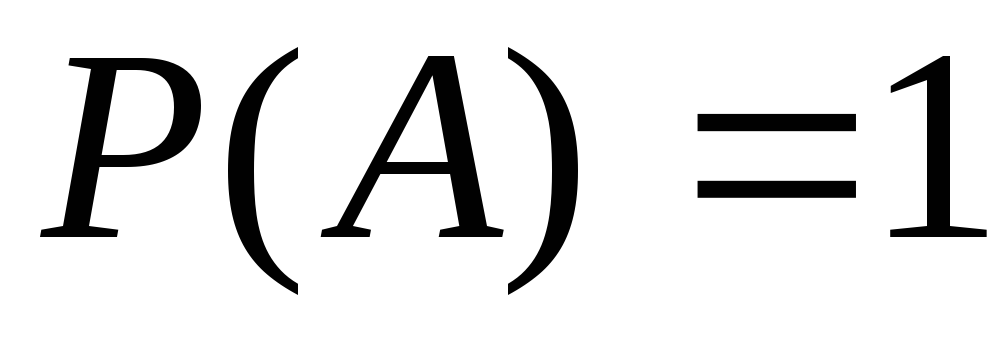 ,
то событие
,
то событие достоверное.
достоверное.Равновозможные элементарные события являются равновероятными, т.е. обладают одной и той же вероятностью.
Теорема.
Эквивалентные события имеют
одинаковые вероятности, т.е. если
![]() ,
то
,
то![]() .
.
Доказательство.
Действительно, каждый элементарный
исход события![]() является таким же элементарным исходом
для события
является таким же элементарным исходом
для события![]() и наоборот. В силу формулы
и наоборот. В силу формулы![]() справедливо равенство
справедливо равенство
![]() .
.
Если событие
![]() происходит всякий раз после того, как
произошло событие
происходит всякий раз после того, как
произошло событие![]() ,
то говорят, что из события
,
то говорят, что из события![]() следует событие
следует событие![]() (
(![]() ).
Например, для любых двух событий
).
Например, для любых двух событий![]() и
и![]() справедливо
справедливо![]() и
и![]() .
.
Теорема. Если
![]() ,
то
,
то![]() .
.
Доказательство.
Пусть![]() и
и![]() – число благоприятных элементарных
исходов соответственно для событий
– число благоприятных элементарных
исходов соответственно для событий![]() и
и![]() ,
а
,
а![]() – общее число элементарных исходов.
Так как каждый элементарный исход для
события
– общее число элементарных исходов.
Так как каждый элементарный исход для
события![]() является также элементарным исходом
для события
является также элементарным исходом
для события![]() ,
то
,
то![]() и, следовательно,
и, следовательно,![]() .Пример: выпадение четного числа
очков более вероятно, чем выпадение
двойки.
.Пример: выпадение четного числа
очков более вероятно, чем выпадение
двойки.
Теорема. Вероятность
события ![]() ,
противоположного событию
,
противоположного событию ![]() равна
равна
![]() .
.
Доказательство.
Пусть полная система равновозможных
элементарных исходов содержит![]() событий, из которых
событий, из которых![]() (
(![]() ),
благоприятны событию
),
благоприятны событию![]() .
Тогда
.
Тогда![]() исходов неблагоприятны событию
исходов неблагоприятны событию![]() ,
т.е. благоприятствуют событию
,
т.е. благоприятствуют событию![]() .
Таким образом,
.
Таким образом,
![]() .
.
Классическое определение вероятности предполагает, что
число элементарных исходов конечно;
эти исходы равновозможны.
Однако на практике встречаются испытания с бесконечным числом возможных исходов. Кроме того, нет общих методов, позволяющих результат испытания, даже с конечным числом исходов, представить в виде суммы равновозможных элементарных исходов. Поэтому применение классического определения вероятности весьма ограничено. Пример: кубик со смещенным центром тяжести.
