Распределение Пуассона.

Ранее отмечалось, что если при увеличении числа испытаний произведение остается постоянным, то биномиальное распределение при больших значенияхn сходится к распределению Пуассона.

Случайная величина называетсяраспределенной по закону Пуассона, если она может принимать значения , соответствующая вероятность которых определяется по формуле Пуассона: ,

Распределение Пуассона для приведено ниже

Для распределения Пуассона математическое ожидание и дисперсия равны соответственно:

.

Равенство значений математического ожидания и дисперсии является уникальным свойством распределения Пуассона. Это свойство часто применяется на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина X распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики случайной величины – математическое ожидание и дисперсию. Если их значения близки, то это может служить доводом в пользу гипотезы о пуассоновском распределении.

Геометрическое распределение

Дискретная случайная величина имеет геометрическое распределение, если она принимает значения(счетное множество значений) с вероятностями

.

Случайная величина, имеющая геометрическое распределение, представляет собой число испытаний в схеме Бернулли до первого успеха. Геометрическое распределение для некоторых конкретных значений p приведено ниже

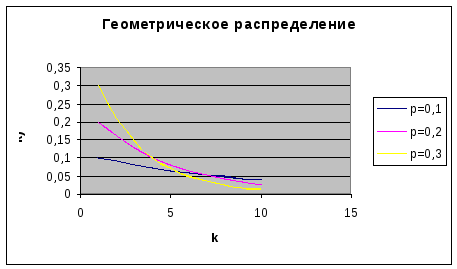
Можно показать, что математическое ожидание и дисперсия для геометрического распределения равны соответственно:

Пример. В большой партии изделий вероятность брака равна . Контроль качества проводится до первого появления бракованного изделия. В результате серии проверок обнаружилось, что бракованное изделие впервые появлялось в среднем при десятом испытании. Оценить численное значение.

Решение. Пусть - число испытаний до первого появления бракованного изделия. Эта случайная величина имеет геометрическое распределение. По условию ее среднее значение равно. Таким образом

Гипергеометрическое распределение (урновая схема)

Дискретная случайная величина имеет гипергеометрическое распределение, если она принимает значенияс вероятностями

представляет вероятность выбораобъектов, обладающих заданным свойством, из множестваобъектов, случайно извлеченных (без возврата) из совокупностиобъектов, среди которыхобъектов обладают заданным свойством. Ниже приведен пример графика гипергеометрического распределения.

Математическое ожидание и дисперсия случайной величины, имеющей гипергеометрическое распределение с параметрами равны:

Пример. Имеется 5 фирм, у трех из которых отчетность оформлена неправильно. 2 ревизора проверяют 2 произвольно выбранные фирмы. Какова вероятность того, что при проверке будет обнаружена неправильная отчетность а) ни в одной, б) в одной, в) в двух фирмах?

Решение. Данная задача может быть решена с помощью гипергеометрического распределения. По условию задачи общее число объектов (фирм) равно N = 10, число фирм с неправильной отчетностью M=3. Проверяется всего две фирмы (n =2). Число фирм с неправильной отчетностью среди двух выбранных – величина переменная (m=0, 1, 2). Таким образом, имеем

а) (ни одной неправильной отчетности)

б) (одна неправильная отчетность)

в) (две неправильные отчетности).