
- •Пространство элементарных событий.
- •Совместные и несовместные события.
- •Операции над событиями (сумма, разность, произведение).
- •Свойства операций над событиями.
- •Алгебра и сигма-алгебра событий.
- •Классическое определение вероятности события. Случаи равновероятных исходов.
- •Статистическое определение вероятности события. Случаи неравновероятных исходов.
- •Геометрические вероятности.
- •Аксиоматическое построение теории вероятностей.
- •Полная группа событий.
- •Условная вероятность.
- •Независимость событий.
- •Основные понятия комбинаторики.
- •Правила суммы и произведения.
- •Случай непостоянной вероятности появления события в опытах
- •Для того чтобы найти вероятность появления события ровно раз в серииопытов, достаточно произвести перемножение сомножителей в производящей функции. Коэффициент при членеи даст искомую вероятность.
- •Предельные теоремы для схемы Бернулли.
- •Теорема Пуассона.
- •Понятие потока событий.
- •Локальная теорема Муавра –Лапласа.
- •Интегральная (глобальная) теорема Муавра – Лапласа.
- •Закон распределения дискретной случайной величины.
- •Свойства функции распределения
- •Свойства математического ожидания:
- •Дисперсия случайной величины и ее свойства.
- •Среднее квадратическое отклонение.
- •Распределение Пуассона.
- •Геометрическое распределение
- •Гипергеометрическое распределение (урновая схема)
- •Равномерное распределение.
- •Показательное распределение.
- •Свойства функции Гаусса.
- •Вероятность попадания нормальной случайной величины в заданный интервал.
- •Где - функция Лапласа.
- •Функция Лапласа и ее свойства.
- •Отклонение нормальной случайной величины от ее математического ожидания. Правило «трех сигм».
- •Закон распределения вероятностей двумерной случайной величины
- •Свойства совместной функции распределения двух случайных величин
- •Плотность совместного распределения вероятностей непрерывной двумерной случайной величины
- •Свойства двумерной плотности вероятности
- •Независимые случайные величины
- •Для независимых случайных величин справедливы соотношения
- •Корреляционный момент
- •Коэффициент корреляции Коэффициентом корреляции случайных величинX и y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:
- •Свойства коэффициента корреляции
- •Способы отбора На практике применяются различные способы отбора, которые можно подразделить на два вида:
- •Выборочные среднее и дисперсия
- •Статистический критерий
- •A. Понятие о корреляционном анализе
- •Линейная регрессия
- •Множественная линейная регрессия
- •Нелинейная регрессия
- •Однородные цепи Маркова
- •Понятие о системах массового обслуживания
Свойства функции распределения
Приведем ряд свойств функции распределения, непосредственно следующих из ее определения.
Функция распределения принимает значения из промежутка
 :
: .
.Функция распределения – неубывающая функция, т.е.
 при
при .
.Вероятность того, что случайная величина примет значение из полуинтервала
 ,
равна разности
,
равна разности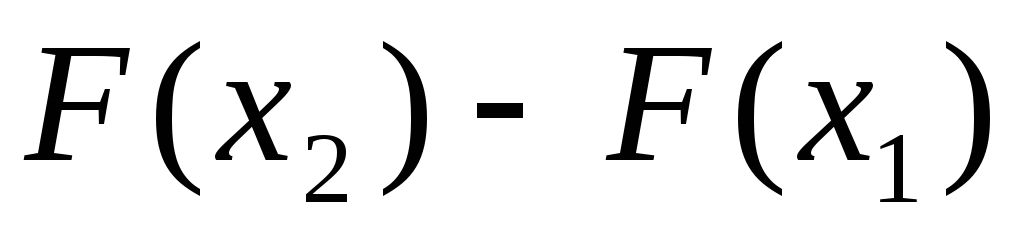 :
:

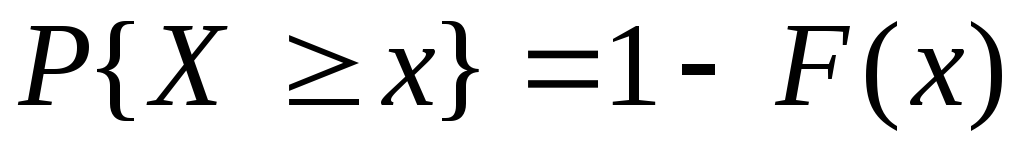 .
.Если
 ,
то
,
то .
.Если
 ,
то
,
то .
.
Плотность распределения вероятностей.
Для непрерывныхслучайных величин, кроме функции распределения вводится также понятие плотности распределения вероятностей, или плотности вероятности.
Плотностью
распределения вероятностей![]() непрерывной случайной величины
непрерывной случайной величины![]() называется производная от ее функции
распределения
называется производная от ее функции
распределения
![]() .
.
Зная
плотность распределения вероятностей,
можно найти функцию распределения,
интегрируя плотность вероятности в
общем случае от
![]() до рассматриваемого значения
до рассматриваемого значения![]() ,
т.е.
,
т.е.
![]() .
.
Свойства плотности распределения вероятностей
Действительно,
так как функция распределения
![]() неубывающая функция, то ее производная
– функция неотрицательная
неубывающая функция, то ее производная
– функция неотрицательная
Несобственный интеграл от плотности распределения вероятностей в пределах от
 до
до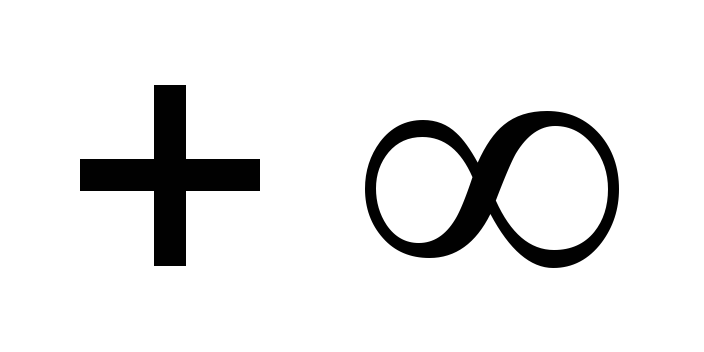 равен единице:
равен единице:
![]()
Действительно,
данный несобственный интеграл выражает
вероятность события, состоящего в том,
что случайная величина примет значение,
принадлежащее интервалу
![]() .
Т.к. такое событие достоверно, то его
вероятность равна единице.
.
Т.к. такое событие достоверно, то его
вероятность равна единице.
Вероятностный смысл плотности распределения вероятностей: вероятность того, что случайная величина примет значение, принадлежащее интервалу (x,x+dx) приближенно равна произведению плотности вероятности в точкеxна ширину интервалаdx.
Пример. Пусть дальность полета снаряда при определенной установке прицела описывается плотностью распределения вида

Какова
вероятность того, что при одном выстреле
будет получен перелет в пределах от 10
д0 20 метров? Ответ:
![]()
Лекция 7. Математическое ожидание случайной величины и его свойства. Дисперсия случайной величины, ее свойства. Среднее квадратическое отклонение.
Во многих практических случаях информация о случайной величине, которую дают закон распределения, функция распределения или плотность вероятностей, является избыточной. Часто проще и удобнее пользоваться числами, которые описывают случайную величину суммарно. К числу наиболее важных из таких числовых характеристик случайных величин относятся математическое ожидание,дисперсияисреднее квадратическое отклонение.
Математическое ожидание случайной величины
Математическое ожидание характеризует среднее ожидаемое значение случайной величины, т.е. приближенно равно ее среднему значению (вероятностный смысл математического ожидания). Иногда знания этой характеристики достаточно для решения задачи. Например, при оценке покупательной способности населения вполне может хватить знания среднего дохода, при анализе выгодности двух видов деятельности можно ограничиться сравнением их средних прибыльностей. Знание того, что выпускники данного университета зарабатывают в среднем больше выпускников другого, может послужить основанием для принятия решения о поступлении в данный ВУЗ и т.п.
Математическое ожидание дискретнойслучайной величины определяется соотношением:
![]() ,
где
,
где
![]() .
.
Математическое ожидание непрерывнойслучайной величины равно
![]()
где
![]() - плотность вероятности.
- плотность вероятности.
Свойства математического ожидания
Прежде
чем формулировать свойства математического
ожидания необходимо пояснить смысл
арифметических операций
![]() ,
,![]() ,
,![]() и т.п., где
и т.п., где![]() и
и![]() – дискретные случайные величины.
– дискретные случайные величины.
Например,
под суммой
![]() понимается случайная величина
понимается случайная величина![]() ,
значениями которой являются все
допустимые суммы
,
значениями которой являются все
допустимые суммы![]() ,
где
,
где![]() и
и![]() – все возможные значения соответственно
случайных величин
– все возможные значения соответственно
случайных величин![]() и
и![]() .
.
