Способы отбора На практике применяются различные способы отбора, которые можно подразделить на два вида:

• Отбор, не требующий расчленения генеральной совокупности на части. Сюда относятся а) простой случайный бесповторный отбор и б) простой случайный повторный отбор.

• Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся а) типический отбор, б)механический отбори в)серийный отбор.

Простым случайнымназывают отбор, при котором объекты извлекаются по одному из генеральной совокупности. Осуществить такой отбор для генеральной совокупности изNобъектов можно, например, посредством записи на карточках номеров от 1 доN, последующем перемешиванием карточек и выниманием их наугад. При этом обследованию подлежат объекты, имеющие номера, совпадающие с номерами карточек. Если карточки возвращаются в пачку, то имеем простую случайную повторную выборку, в противном случае – простую бесповторную. При большом объеме генеральной совокупности более рациональным является использование таблиц случайных чисел. Например, чтобы выбрать 50 объектов из пронумерованной генеральной совокупности, открывают любую страницу таблицы случайных чисел и выписывают 50 чисел подряд; в выборку попадают те объекты, номера которых совпадают с выписанными случайными числами. Если случайное число таблицы превосходит числоN, такое число пропускают. При проведении бесповторной выборки пропускают также случайные числа, уже встречавшиеся раньше.

Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее “типической” части. Например, если детали изготовлены на нескольких станках, то отбор производят из продукции каждого станка в отдельности.

Механическим называют отбор, при котором генеральная совокупность механически делится на столько групп, сколько объектов должно войти в выборку, а из каждой группы выбирается один объект. Например, если нужно отобрать 20% изготовленных станком деталей, то отбирают каждую пятую деталь.

Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а “сериями”, которые подвергаются сплошному обследованию. Например, если изделия производятся большой группой станков-автоматов, то подвергают сплошному обследованию продукцию только нескольких станков. Этим видом отбора пользуются тогда, когда обследуемый признак колеблется в различных сериях незначительно.

На практике часто применяют комбинированный отбор, при котором сочетаются указанные выше способы. Например, разбивают генеральную совокупность на серии одинакового объема, затем простым случайным отбором выбирают несколько серий и, наконец, из каждой серии простым случайным отбором извлекают отдельные объекты.

Вариационный ряд для дискретных и непрерывных случайных величин.

Пусть из генеральной совокупности извлечена выборка, причем значение исследуемого параметра наблюдалосьраз,-раз и т.д. При этом

объем выборки. Наблюдаемые значения называютвариантами, а последовательность вариант, записанных в возрастающем порядке –вариационным рядом. Числа наблюдений называютчастотами, а их отношения к объему выборки - относительными частотами. Вариационный ряд можно представить таблицей :

X			…..
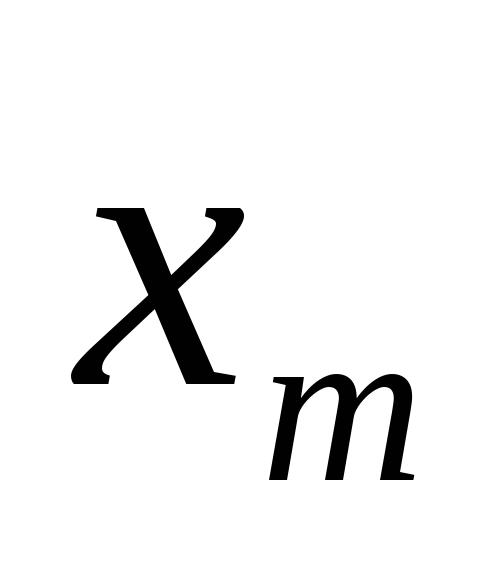
n			….

Статистическим распределением выборки называют перечень вариант и соответствующих им относительных частот. Статистическое распределение можно представить как

X			…..
w			….

где относительные частоты .

Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями,а в математической статистике – соответствие между наблюдаемымивариантамии ихчастотамиилиотносительными частотами.

Приведенный способ представления статистических данных применяют в случае дискретных случайных величин. Для непрерывных случайных величин удобнее разбить отрезок [a,b] возможных значений случайной величины на частичные полуинтервалы(замкнут также и справа) с помощью некоторой системы точек. Часто разбиение [a,b] производят на равные части, тогда, где

В качестве частот теперь надо брать количество наблюдаемых значений, попавших на каждый из частичных интервалов. Вариационный ряд имеет в таком случае вид

X			…..
n			….

а статистическое распределение –

X			…..
n			….

Число интервалов часто выбирают на основании формулы Стерджерса.

Полигон и гистограмма

Графически статистическое распределение представляется в частности, с помощью полигонаигистограммы.

Полигоном частотназывают ломаную линию, отрезки которой соединяют точки. Для построения полигона частот на оси абсцисс откладывают варианты, а на оси ординат – соответствующие им частотыи соединяют точкиотрезками прямых.

Полигон относительных частот строится аналогично, за исключением того, что на оси ординат откладываются относительные частоты.

В случае непрерывного признака строится гистограмма, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длинойhи находят для каждого частичного интервала- сумму частот вариант, попавших вi– й интервал.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которой служат частичные интервалы длиноюh, а высоты равны отношению. Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии (высоте). Площадьi-го прямоугольника равна- сумме частот вариантi–го интервала, поэтому площадь гистограммы частот равна сумме всех частот, т.е.объему выборки.

В случае гистограммы относительныхчастот по оси ординат откладываются относительные чатоты, на оси абсцисс – частичные интервалы, над ними проводят отрезки, параллельные оси абсцисс на высоте. Площадьi-го прямоугольника равна относительной частоте вариант, попавших вi-й интервал. Поэтому площадь гистограммы относительных частот равна сумме всех относительных частот, то естьединице.

Лекция 13. Понятие о статистических оценках случайных величин

Эмпирическая функция распределения

Пусть известно статистическое распределение частот количественного признака X. Обозначим черезчисло наблюдений, при которых наблюдалось значение признака, меньшееxи черезn– общее число наблюдений. Очевидно, относительная частота событияX<xравнаи является функциейx. Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.

Эмпирической функцией распределения(функцией распределения выборки) называют функцию, определяющую для каждого значенияxотносительную частоту событияX<x. Таким образом, по определению,где- число вариант, меньшихx,n– объем выборки.

В отличие от эмпирической функции распределения выборки, функцию распределения генеральной совокупности называюттеоретической функцией распределения. Различие между этими функциями состоит в том, что теоретическая функция определяетвероятность событияX<x, тогда как эмпирическая –относительную частоту этого же события.

При росте nотносительная частота событияX<x, т.е.стремится по вероятности к вероятностиэтого события. Иными словами

Свойства эмпирической функции распределения:

1. Значения эмпирической функции принадлежат отрезку [0,1]

2. - неубывающая функция

3. Если - наименьшая варианта, то= 0 при, если- наибольшая варианта, то=1 при.

Эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

Пример. Построим эмпирическую функцию по распределению выборки:

Варианты	2	6	10
Частоты	12	18	30

Найдем объем выборки: 12+18+30=60. Наименьшая варианта равна 2, поэтому =0 приx£2. Значениеx<6, т.е., наблюдалось 12 раз, следовательно,=12/60=0,2 при 2<x£6. Аналогично, значенияX< 10, т.е.инаблюдались 12+18=30 раз, поэтому=30/60 =0,5 при 6<x£10. Так какx=10 – наибольшая варианта, то=1 приx> 10. таким образом, искомая эмпирическая функция имеет вид:

Важнейшие свойства статистических оценок

Пусть требуется изучить некоторый количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак и необходимо оценить параметры, которыми оно определяется. Например, если изучаемый признак распределен в генеральной совокупности нормально, то нужно оценить математическое ожидание и среднее квадратическое отклонение; если признак имеет распределение Пуассона – то необходимо оценить параметр l.

Обычно имеются лишь данные выборки, например значения количественного признака , полученные в результатеnнезависимых наблюдений. Рассматриваякак независимые случайные величиныможно сказать, чтонайти статистическую оценку неизвестного параметра теоретического распределения – значит найти функцию от наблюдаемых случайных величин, которая дает приближенное значение оцениваемого параметра. Например, для оценки математического ожидания нормального распределения роль функции выполняет среднее арифметическое

Для того чтобы статистические оценки давали корректные приближения оцениваемых параметров, они должны удовлетворять некоторым требованиям, среди которых важнейшими являются требования несмещенностиисостоятельности оценки.

Пусть - статистическая оценка неизвестного параметратеоретического распределения. Пусть по выборке объемаnнайдена оценка. Повторим опыт, т.е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным получим другую оценку. Повторяя опыт многократно, получим различные числа. Оценкуможно рассматривать как случайную величину, а числа- как ее возможные значения.

Если оценка дает приближенное значениес избытком, т.е. каждое числобольше истинного значениято, как следствие, математическое ожидание (среднее значение) случайной величиныбольше, чем:. Аналогично, еслидает оценкус недостатком, то.

Таким образом, использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, привело бы к систематическим (одного знака) ошибкам. Если, напротив, , то это гарантирует от систематических ошибок.

Несмещеннойназывают статистическую оценку, математическое ожидание которой равно оцениваемому параметрупри любом объеме выборки.

Смещеннойназывают оценку, не удовлетворяющую этому условию.

Несмещенность оценки еще не гарантирует получения хорошего приближения для оцениваемого параметра, так как возможные значения могут бытьсильно рассеянывокруг своего среднего значения, т.е. дисперсияможет быть значительной. В этом случае найденная по данным одной выборки оценка, например, может оказаться значительно удаленной от среднего значения,а значит, и от самого оцениваемого параметра.

Эффективнойназывают статистическую оценку, которая, при заданном объеме выборкиn, имеетнаименьшую возможную дисперсию.

При рассмотрении выборок большого объема к статистическим оценкам предъявляется требование состоятельности.

Состоятельнойназывается статистическая оценка, которая приn®¥стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки приn®¥стремится к нулю, то такая оценка оказывается и состоятельной.