Закон распределения вероятностей двумерной случайной величины

Законом распределениядискретной двумерной случайной величиныназывают перечень возможных значений этой величины, т.е. пар чисел, гдеи– возможные значения величини, соответственно, и вероятностейих совместного появления.

Двумерная дискретная случайная величина задается в видетаблицы распределения вида:

где первая строка таблицы указывает возможные значения составляющей , а первый столбец – все возможные значения составляющей.

Так как события (;) образуют полную группу, то.

Зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения каждой из ее составляющих. Так, например, вероятность того, что примет значение, равна.

Совместная функция распределения двух случайных величин

Функция , определяющая для каждой пары чиселвероятность того, чтопримет значение меньшее, и при этомпримет значение меньшее, называетсясовместной функцией распределениядвух случайных величин=.

Геометрически это равенство можно истолковать так: – это вероятность того, что случайная точка () попадет в бесконечный квадрант с вершиной (), расположенный левее и ниже этой вершины.

Свойства совместной функции распределения двух случайных величин

1. Значения совместной функции распределения удовлетворяют неравенству:

.

2. –неубывающая функция по каждому аргументу, т.е.

, если ;

, если .

Совместная функция распределения имеет следующие предельные значения:

;;

;.

3. При илисовместная функция распределения системы становится функцией распределения одной из составляющих:;

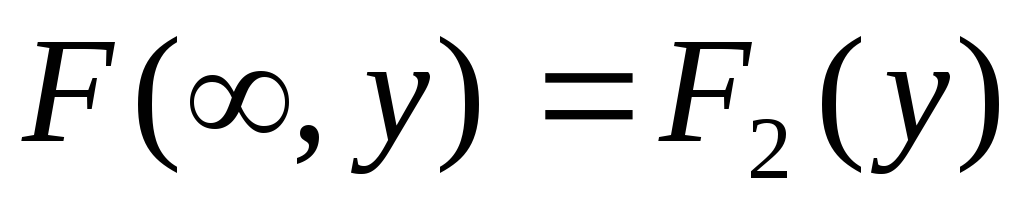
Плотность совместного распределения вероятностей непрерывной двумерной случайной величины

Непрерывную двумерную случайную величину можно задать с помощью плотности распределения. Плотность совместного распределения вероятностейдвумерной непрерывной случайной величины (,) – это вторая смешанная частная производная от функции распределения:

.

Зная плотность совместного распределения , можно найти совместную функцию распределенияпо формуле

следующей из определения плотности распределения двумерной непрерывной случайной величины (,).

Смысл плотности совместного распределения вероятностей: вероятность попадания случайной точки в прямоугольник (с вершиной в точке и сторонамииравна произведению, когда стороны этого прямоугольника стремятся к нулю.

В связи с этим, вероятность попадания случайной точки в произвольную область D равна двойному интегралу по областиDот функции:

Свойства двумерной плотности вероятности

1. Двумерная плотность вероятности неотрицательна: .

2. Двойной несобственный интеграл с бесконечными пределами от двумерной плотности вероятности равен единице:.

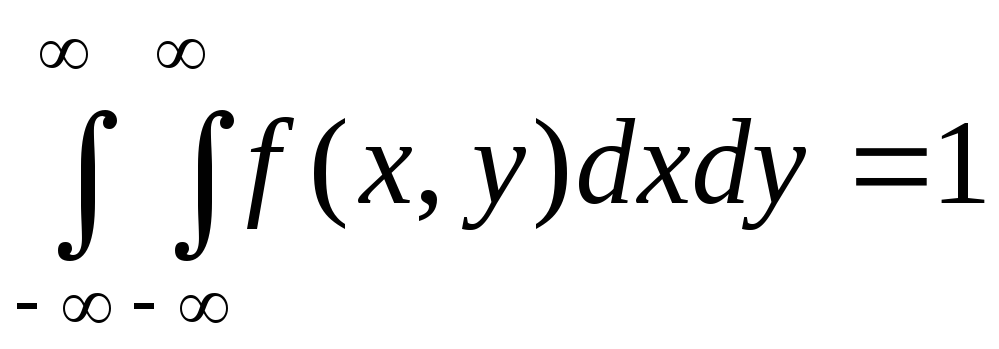Независимые случайные величины

Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.

Теорема. Для того чтобы случайные величиныибыли независимыми, необходимо и достаточно, чтобы функция распределения системы (,) была равна произведению функций распределения составляющих:.

Следствие.Для того чтобы случайные величиныибыли независимыми, необходимо и достаточно, чтобы плотность совместного распределения системы (,) была равна произведению плотностей распределения составляющих:.