21. Частные производные высших порядков, смешанные производные (с демонстрацией на конкретных примерах). Теорема о смешанных производных (для функции двух переменных и общий случай).

2ой Производной ф-и называется производная от 1й производной ф-и.

(диф-ом 2го порядка ф-и z=f(x,y) называется диф-ал от диф-ала 1го порядка)

Вторые смешанные производные ф-и f=z(x,y) при условии их непрерывности равны меду собой: .

Пусть ф-я z=f(x₁,,…,x_n) определена и непрерывна в открытой n-мерной области d и имеет в этой области всевозможные частные производные до (k-1)-порядка включительно и смешанные производные k-го порядка. Причем все эти производные не зависят от того порядка, в котором производится последовательное дифференцирование.

22. Производная по направлению, градиент функции.

Производной z’_l по направлению l ф-и 2х переменных z=f(x,y) называется предел отношения приращения ф-и в этом направлении к величине перемещения Δl при стремлении последней к нулю, т.е. Производная z’_l характеризует скорость изменения ф-и в направлении l. Производная по направлению может быть выражена через частные производные по формуле где единичный вектор задает направление l (c углами α и β, образуемыми с осями координат).

Градиентом функции z=f(x,y) называется вектор . Производная по направлению есть скалярное произведение градиента и единичного вектора e, задающего направление l.

Градиент ф-и задает направление наибольшего роста z, а его длина - скорость изменения ф-и z в этом направлении. Градиент ф-и в точке М(х,у), отличный от нуля, перпендикулярен линии уровня, проходящей через эту точку.

23. Дифференциалы первого и высших порядков функции двух переменных.

Дифференциалом ф-и z=f(x,y) называется сумма произведений частных производных этой ф-и на приращения независимых переменных

Ф-я z=f(x,y) называется диф-ой в точке (х,у), если ее полное приращение может быть представлено в виде бесконечно малые величины при Δх→0, Δу→0.

Диф-ал ф-и 2х переменных, как и в случае одной переменной, представляет главную, линейную относительно Δх и Δу, часть полного прираще7ния ф-и. Геометрически диф-ал dz есть приращение аппликаты касательной плоскости к поверхности z=f(x,y) к данной точке, когда переменная (х,у) получают приращение (Δх,Δу).

Необходимое условие диф-ти: если ф-я z=f(x,y) диф-ма в точке (х,у), то она имеет в этой точке частные производные по х и по у, причем .

Достаточное условие диф-ти: если ф-я z=f(x,y) имеет частные производные не только в некоторой точки (х,у), но и в некоторой ее окрестности и эти производные непрерывны в самой точке (х,у), то ф-я диф-ма в точке (х,у).

Диф-ом 2го порядка ф-и z=f(x,y) называют диф-ал от диф-ла 1го порядка.

24. Необходимое условие экстремума дифференцируемой функции нескольких переменных с демонстрацией на конкретном примере.

Пусть ф-я z=f(x,y) определена и непрерывна в некоторой области и точка (х,у) принадлежит этой области. Тогда, точка (х_о,у_о) – точка локального max (min), если всюду в некоторой окрестности этой точки выполняется неравенство:

.

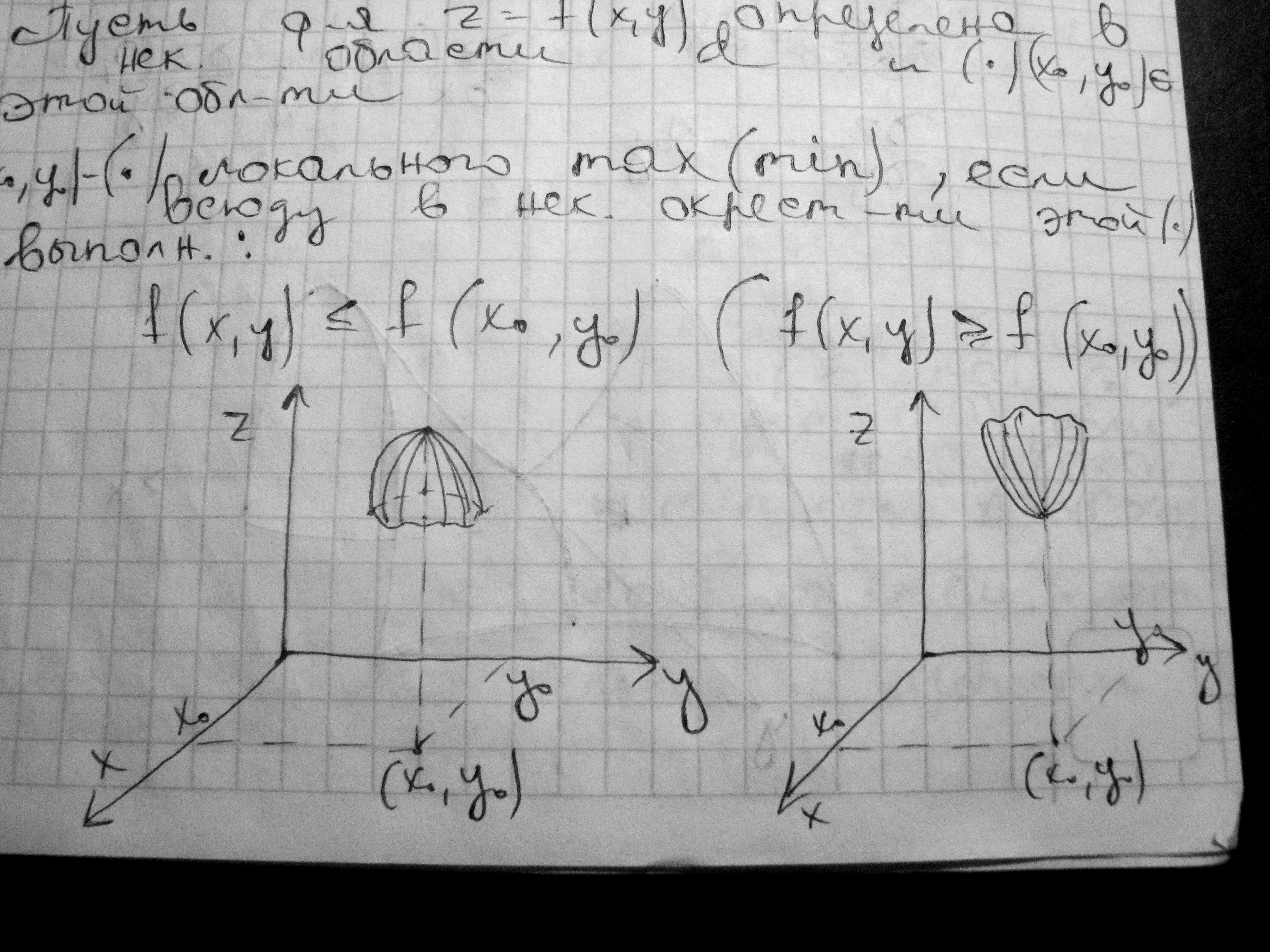Необходимое условие экстремума. Если в точке экстремума все частные производные сущ-ют и непрерывны, то они равны нулю в этой точке.

Точки, в которых выполнено необходимое условие экстремума ф-и называются критическими или стационарными.

Например,