
- •1*. Понятие приращения функции и понятие производной. Геометрический и физический смысл производной.
- •2. Определения касательной и нормали и их уравнения.
- •3*. Правила вычисления производных с демонстрацией на конкретных примерах.
- •4*. Производная сложной функции с демонстрацией на конкретных примерах.
- •5 . Производная обратной функции с демонстрацией на конкретных примерах.
- •6. Производная неявной функции и функции, заданной параметрически с демонстрацией на конкретных примерах.
- •7. Производная степенно-показательного выражения с демонстрацией на конкретных примерах.
- •8*. Первый дифференциал. Инвариантность формы первого дифференциала.
- •9. Производные и дифференциалы высших порядков. Формула Лейбница (с демонстрацией на примерах).
- •10. Раскрытие неопределенностей. Правило Лопиталя (с демонстрацией на примерах).
- •11. Формула Тейлора для многочлена и произвольной ф-ии
- •12. Теоремы Ферма, Ролля, Лагранжа, Коши (с геометр интерпретацией)
- •13. Понятие монотонности и экстремума ф-и с геометр интерпретацией и примерами
- •15*. Необходимые и достаточные условия экстремума функции с геометрической интерпретацией и конкретынми примерами.
- •16. Необходимое и достаточное условия выпуклости (вогнутости) графика функции. Точки перегиба и геометрический смысл перегиба. Схема нахождения точек перегиба с демонстрацией на конкретных примерах.
- •17. Асимптоты и способы их отыскания с демонстрацией на конкретных примерах
- •18*. Понятие функции нескольких переменных (с примерами). Линии уровня. Нахождение линий уровня на конкретном примере.
- •19. Определение предела и непрерывности функции нескольких переменных (привести примеры).
- •20. Полное приращение функции нескольких переменных. Определение частной производной с геометрической интерпретацией. Вычисление частных производных на конкретных примерах.
- •21. Частные производные высших порядков, смешанные производные (с демонстрацией на конкретных примерах). Теорема о смешанных производных (для функции двух переменных и общий случай).
- •22. Производная по направлению, градиент функции.
- •23. Дифференциалы первого и высших порядков функции двух переменных.
- •24. Необходимое условие экстремума дифференцируемой функции нескольких переменных с демонстрацией на конкретном примере.
- •25. Достаточное условие экстремума функции двух переменных с демонстрацией на конкретном примере.
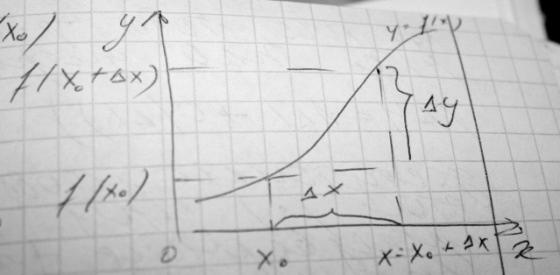
1*. Понятие приращения функции и понятие производной. Геометрический и физический смысл производной.
Если y=f(x) опреелена на X, xo∈X, а x= xo +∆x ∈X, то ∆x= x- xo - приращение аргумента,
∆у= ∆f(xo) = f(xo +∆x) – f(xo) – приращение функции
Производная функцией f(x) по независимой переменной x в точке xo - предел отношения преращения ф-ии ∆f(xo) к приращению аргумента ∆x при ∆x→0, если этот предел существует.
F’(xo)
= ![]()
Геометрически производная = угловому коэффициенту ксательной к графику функции в точке xo: k= tg'α=f’(xo), α-угол наклона касательной.
Уравнение касательной в ее точке пересечения с кривой y(x) (в т.A(xo, yo)): y- yo= f’(xo)(x- xo)
Уравнение
нормали: y- yo
= ![]()
f’(xo)
характеризует скорость изменения f(x)
в точке xo
- мгновенная скорость.
2. Определения касательной и нормали и их уравнения.
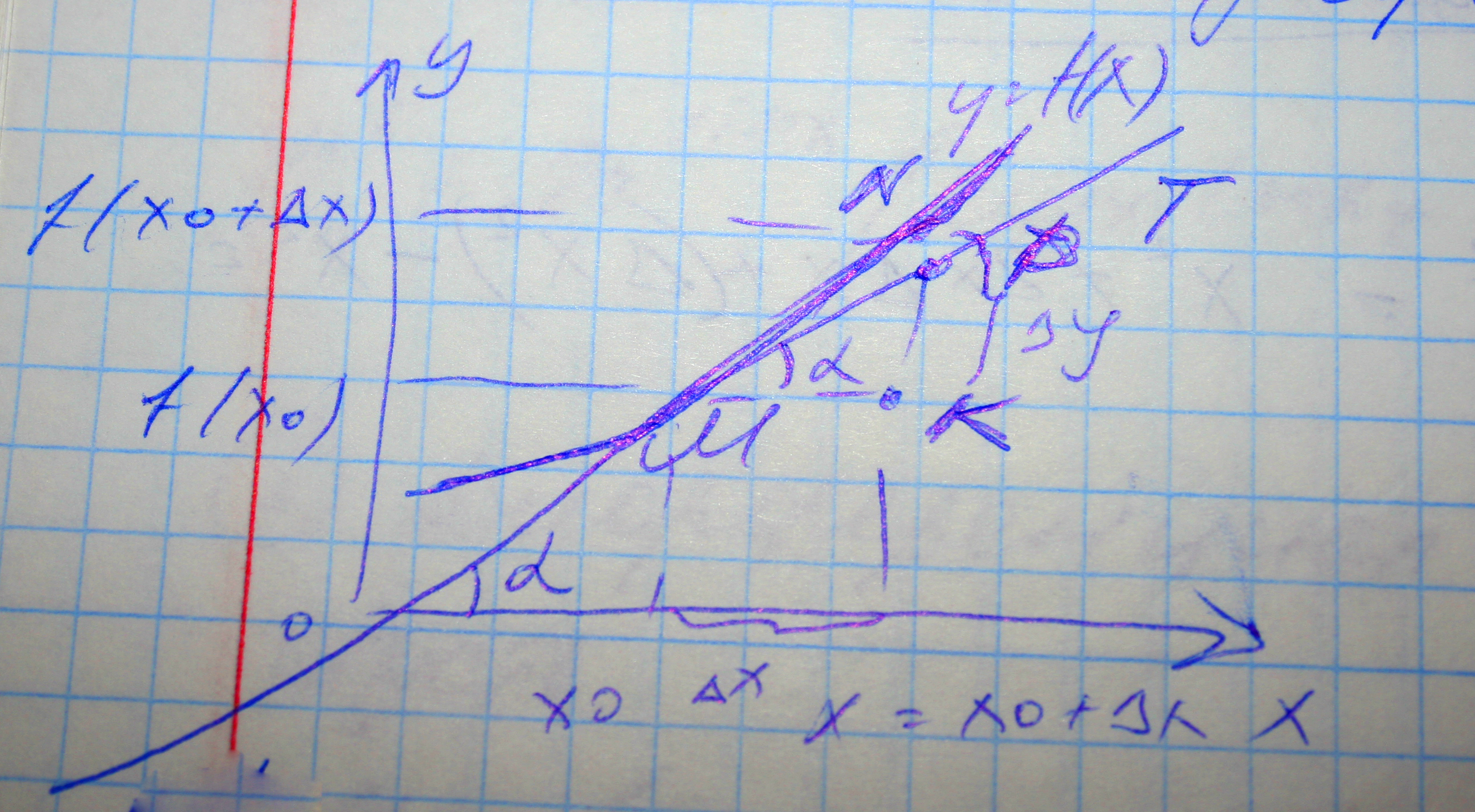
Касательная к кривой y(f) в точке M0(x0, f(x0)) – предельное положение секущей MN при неограниченном приближении N по кривой к M.
y-f(x0)= f’(x0)(x-x0) – ур-е касательной
Производная- это tg угла наклона (угл.коэфф) касательной к кривой y= f(x) в точке (x0;f(x0))
K=tgα= f’(x0), α-угол наклона касательной
Н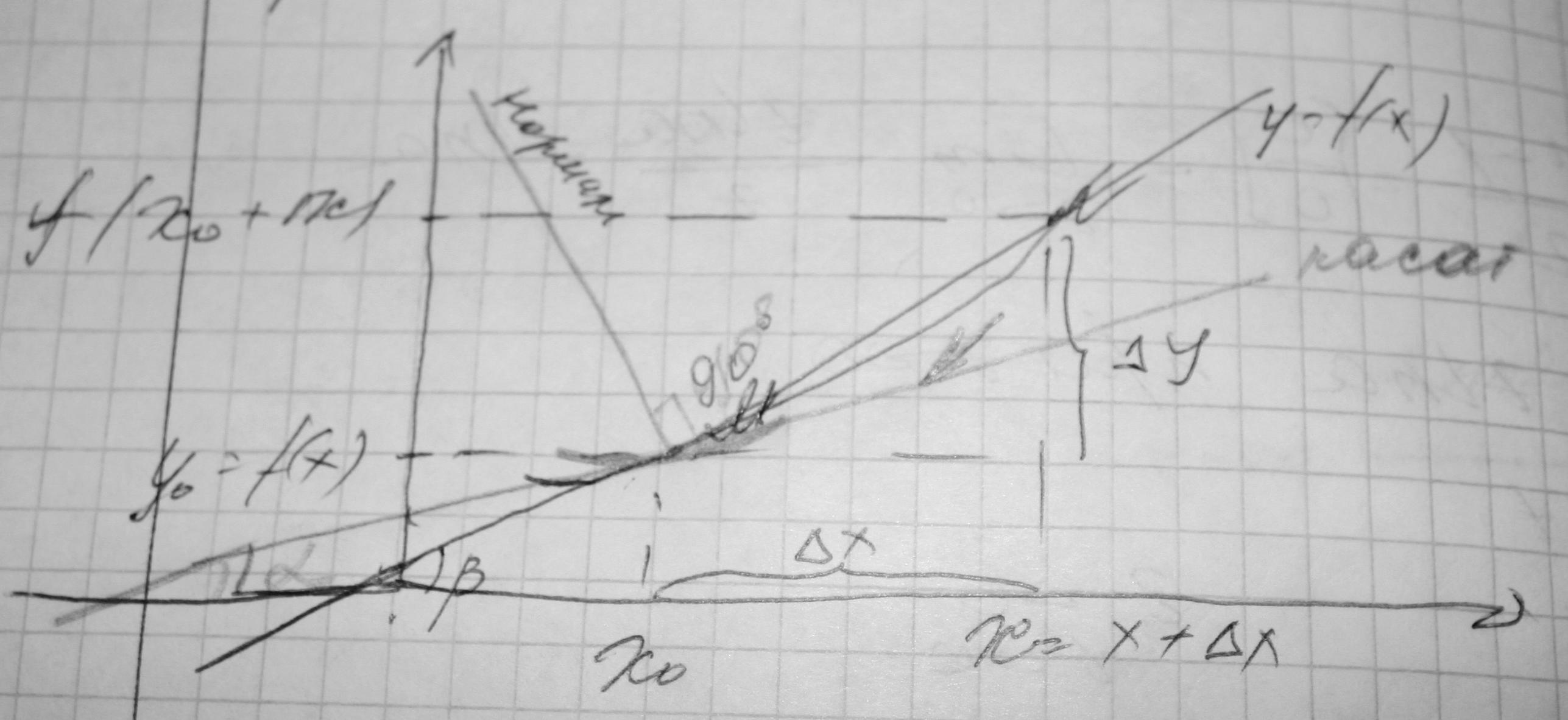 ормаль
к кривой y(f)
в точке M0(x0, f(x0))- прямая, прохожящая через
M и перпендикулярная касательной к
кривой в этой точке.
ормаль
к кривой y(f)
в точке M0(x0, f(x0))- прямая, прохожящая через
M и перпендикулярная касательной к
кривой в этой точке.
k2=1/k1
y-f(x0)= -1/ f’(x0) * (x-x0)
f’(x0) характеризует скорость изменения ф-ии f(x) в точке x0- мгновенная скорость.
3*. Правила вычисления производных с демонстрацией на конкретных примерах.
№ |
Y=f(x) |
Y’=f’(x) |
1 |
C |
0 |
2 |
xm |
mxm-1 |
3 |
ax(0<a≠1) |
axlna |
|
ex |
ex |
4 |
logax (0<a≠1) |
1/x logae |
|
lnx |
1/x |
5 |
sinx |
cosx |
6 |
cosx |
-sinx |
7 |
tgx |
1/cos2x |
8 |
ctgx |
-1/sin2x |
9 |
arcsinx |
1/√1-x2 |
10 |
arccosx |
-1/√1-x2 |
11 |
arctgx |
1/1+x2 |
12 |
arcctgx |
-1/1+x2 |
12 |
√x |
1/2√x |
2)(U±V)’= U’±V’
3)(UV)’=U’V+UV’
4)(U/V)=U’V-UV’ / V2
4*. Производная сложной функции с демонстрацией на конкретных примерах.
Если функция u=f(x) имеет в некоторой точке x производную (∃u'x=u’(x))
Если y=f(u) имеет в соответствующей точке u производную (∃y’u= f’(u))
то y = f(u(x))в точке х также будет иметь производную, равную произведению производной u’(х) и y'(u) ф-й f(u) и u(x).
Y'x= y’u*u’x
5 . Производная обратной функции с демонстрацией на конкретных примерах.
Пусть
Ф-я f(x) в точке x= x0 имеет конечную и отличную от нуля производную ∃f'(x0)≠0
Для нее существует однозначная обратная ф-я ∃x=g(y), непрерывная в соответствующей точке y=y0, где y0=f(x0)
Тогда
∃
g'(y0)
= ![]()
y’x=
![]() x’y=
x’y=
![]() f’(x0)=tgα,
α-
угол наклона кас. к ОХ;
f’(x0)=tgα,
α-
угол наклона кас. к ОХ;
g’(y0)=tgβ, β- угол наклона кас. к ОY
α +β=П/2, tgβ=1/ tgα
Пр.
y=![]() ,
y'x=?.
∃x=
,
y'x=?.
∃x=![]() ,
x’y=
,
x’y=![]() ,
y'x=1/
x’y=1/
,
y'x=1/
x’y=1/![]() 1/x*
1/x*![]() .
.
