6. Производная неявной функции и функции, заданной параметрически с демонстрацией на конкретных примерах.
Если
дифференцируемая на некотором интервале
ф-я y=y(x)
задана неявно ур-ем F(x,y)=0,
то ее производную y’(x)
можно найти из ур-я 
где
F(x,y)
рассматривается как сложная ф-я переменной
x.
F'x(x,y)+ F'y(x,y)*y’x=0
y’x=
- 
Если
ф-я y=f(x)
представлена параметрически:
,
то производные первого и второго порядка
y'x и y''xx можно найти по формулам:
y'x=
,
y'’xx=
7. Производная степенно-показательного выражения с демонстрацией на конкретных примерах.
U(x)V(x)- степенно-показательное выражение
1)
y=U(x)V(x)=
=
y’=
*U’(x))
- ф-ла Лейбница-Бернулли
2) y=U(x)V(x)
z=lny
z’=1/y *y’
y’=y*z’
y’=y(lny)’
3) y=U(x)V(x)
y’=
U(x)V(x)*
lnU(x)*V’(x)+V(x) U(x)(V(x)-1)U’(x)=
U(x)V(x)(
lnU(x)*V’(x)+ 
)
8*. Первый дифференциал. Инвариантность формы первого дифференциала.
Е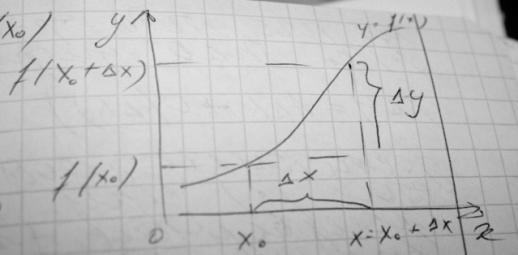
сли
y=f(x)
опреелена на X и непрерывна в токе xo∈X,
∆у= f(xo +∆x) – f(xo), xo +∆x∈ X
Если приращение ф-ии может быть представлено так: ∆y= A∆x+0(∆x), где A- некоторое число, независящее от ∆x, то ф-я f(x) называется дифференцированной в точке x0? А линейная часть этого выражения A∆x наз. Дифференциалом ф-ии в точке х0 и обозначается dy или df(x).
Для того, чтобы функция была дифференцируема, необходимо и достаточно, чтоб для нее в данной точке существовала конечная производная.
Геометрически дифференциал функции- это приращение ординаты касательной, проведенной к графику функции y=f(x) данной точки, когда xo получает приращение ∆x.
Инвариантность(неизменность):
y=f(x) 1) пусть x- независимая переменная dy=f'(x)dx=y’dy
2)пусть x-зависимая переменная, x=φ(t) y=f(φ(t))
dy= y’tdt= y’x*x’tdt=y’xdx
так dy= y’xdx
dx= x’tdt
Форма дифференциала может быть сохранена даже в том случае, если прежняя независимая переменная заменена новой.
9. Производные и дифференциалы высших порядков. Формула Лейбница (с демонстрацией на примерах).
Производная функцией f(x) по независимой переменной x в точке xo - предел отношения преращения ф-ии ∆f(xo) к приращению аргумента ∆x при ∆x→0? Если этот предел существует.
F’(xo)
= 
Производной 2ого порядка ф-ии y=f(x) называется производная от ее производной:
Такой предел. Если он существует, называют 2ой производной.
Производная n-ного порядка- производная от производной (n-1)-го порядка: y(n)=(y(n-1))’
Производные высоких порядков начисляются последовательным дифференцированием ф-ии.
Если
ф-я y=f(x)имеет
конечную производную f’(x)в
т. X, то полное приращение ф-ии
∆y=f(x+∆x)-f(x)=
f’(x)
∆x+𝜶(∆x)∆x,
где 𝜶(∆x)-бесконечно
малая ф-я при ∆x→0,
те
Главная, линейная относительно ∆x, часть полного приращения ф-ии называется дифференциалом ф-ии= dy.
Следовательно, по определению dy=f'(x)∆x. Если f(x)=x, то dx= ∆x, поэтому dy=f’(x)dx.
Дифференциалом 2ого порядка называют d(dy)=d2y=y’’(dx)2.
Дифференциалом n-ого порядка dny=d(dn-1y)=y(n)(dx)n. Отсюда:
y(n)=
Формула Лейбница:
(UV)(n)=
Пр. x=U U’=1 U’’=U’’’=0
ex=V V’=V’’=V’’’= ex
f’’’(x)=
=
+
+
=
+
=3*
ex+
ex=
4ex