10. Раскрытие неопределенностей. Правило Лопиталя (с демонстрацией на примерах).

Пусть ф-ии f(x) и g(x) обращаются в 0 или ∞. Тогда f(x)/g(x) теряет смысл, но lim_x→af(x)/g(x) может существовать. Раскрытие неопределенности [0/0], [∞/∞].

1)пусть ф-ии f(x) и g(x) определены и дифференцируемы в некоторой окрестности (∙)А за исключением, быть может, самой (∙)А.

2)g'(x)≠0 в этой окрестности. f(x) и g(x) являются одновременно бесконечно малыми(lim→0) и бесконечно большими(lim→∞) при x→0.

3)∃ lim_x→af '(x)/g '(x)

Тогда существует предел отношения ф-й ∃ lim_x→af (x)/g(x)= lim_x→af '(x)/g '(x)

Если lim_x→af '(x)/g '(x) не существует, то правило Лопиталя не применяется, но lim_x→af (x)/g(x) может существовать.

[1^∞], [0⁰], [∞⁰]

lim _x→x0 f(x)^g(x)= =

11. Формула Тейлора для многочлена и произвольной ф-ии

Формула Тейлора для многочлена:

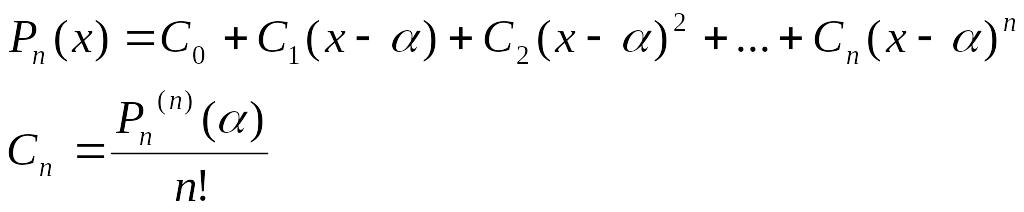
Теорема Тейлора. Пусть ф-я у=f(x) определена в некоторой точке х=а и в некоторой окрестности этой точки ф-я имеет производные до (n+1)-го порядка, тогда сущ-ет х=ξ, такая, что выполняется формула Тейлора:

,

Причем точка ξ лежит между х и а, т.е. ξ=а+α(х-а) и 0<α<1.

Последнее слагаемое в формуле Тейлора называется остаточным членом в форме Лагранжа и обозначается .

Сущ-ет так же остаточный член в форме Пеано, который обозначается: .

При а=0 формула Тейлора называется формулой Маклорена:

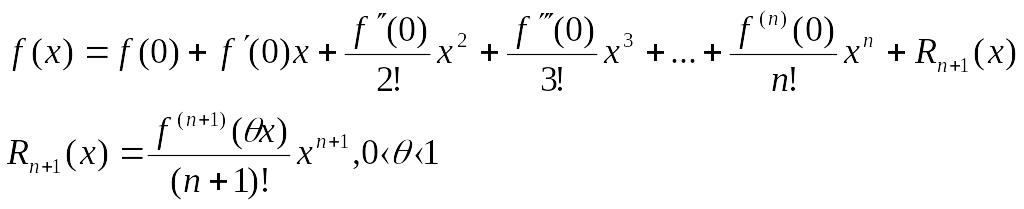
Пример.

12. Теоремы Ферма, Ролля, Лагранжа, Коши (с геометр интерпретацией)

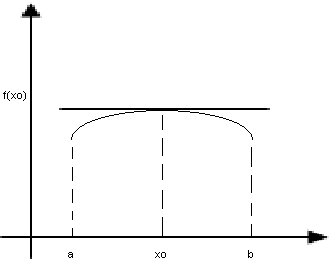
Теорема Ферма. Если ф-я y=f(x) определена на интервале (a,b) и в некоторой внутренней точке x₀ (из (a,b)) принимает наибольшее или наименьшее значение, то производная ф-и в этой точке (если она вообще сущ-ет) равна 0.

З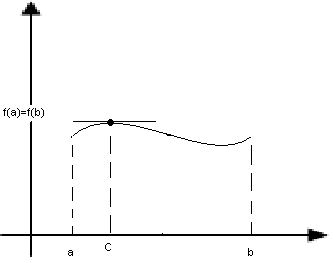 амечание. Теорема неверна, если ф-я рассматривается на отрезке, где она достигает наибольшее (наименьшее) значение на одном из концов.

Теорема Ролля. Пусть ф-я y=f(x):

1)определена и непрерывна на отрезке [a,b]

2)существует ее производная на интервале (a,b)

3)на концах отрезка принимает равные значения, т.е. f(a)=f(b).

Тогда внутри отрезка существует по крайней мере одна такая точка с (принадл (a,b)), в которой производная ф-и равна 0 (f’(c)=0)

Если условия теоремы выполняются, то в точке кривой с ф-и f(c) касательная параллельна оси Ox.

З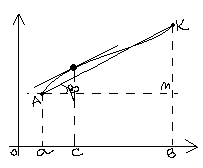 амечание: каждое из условий теоремы явл необходимым.

Теорема Лагранжа. Пусть ф-я y=f(x):

1)определена и непрерывна на отрезке [a,b]

2)существует производная ф-и на интервале (a,b).

Тогда между точками a и b найдется точка с, в которой выполняется равенство .

К графику: f(b)-f(a)=MK, b-a=AM,

Теорема Коши. Пусть ф-и y=f(x) и g(x):

1. непрерывна на отрезке [a,b]

2. существуют конечные производные ф-й на интервале (a,b)

3. g’(x) не равна 0 на (a,b)

тогда внутри отрезка существует по крайней мере одна такая точк5а с (принадл (a,b)), в которой выполняется равенство

13. Понятие монотонности и экстремума ф-и с геометр интерпретацией и примерами

Если производная ф-и f(x) положительна (отрицательна) во всех точках промежутка, то ф-я f(x) монотонно возрастает (убывает) на этом промежутке.

Ф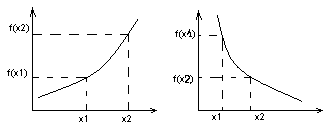 -я f(x) называется возрастающей (убывающей) на промежутке, если для любых двух точек x1 и x2 (x1 меньше x2) этого промежутка справедливо неравенство: f(x1)<f(x2) (f(x1)>f(x2)).

Необходимое условие возр (убыв) ф-и: если диф-мая ф-я y=f(x) возр (убыв) на интервале (a,b), то в любой точке х этого интервала f’(x)≥0 (f’(x)≤0).

Геометрически это означает, что в каждой точке графика возраст ф-и касательная или образует острый угол с осью Ox или параллельная с ней, а в каждой точке графика убывающей ф-и касательная или образует тупой угол с осью Ox или параллельна с ней.

Например, ф-я у=х³ – возрастающая. (f’(0)=0)

Достаточное условие: Если производная диф-ой ф-и положительна (отрицательна) повсюду (т.е. ф-я непрерывно возрастает или убывает повсюду), исключая лишь разве конечное число х, ф-я будет возрастать (убывать). Разделить интервалы непрерывности могут лишь точки, в которых f’(x)=0.

Точка, в которой производная обращается в ноль называется стационарной. Но не каждая стац точка может разделять интервалы монотонности.

Пример. f(x)=x², f’(0)=0, x=0 стац точка

Пример. f(x)=|x|, но f’(0) не существует

Пусть ф-я определена и непрерывна на некотором интервале (a,b) и содержит точку х_о. Точка х_о называется точкой максимума (минимума) ф-и y=f(x), если в некоторой окрестности точки х_о для всех х ≠ х_о выполняется неравенство f(x)≤f(х_о) (f(x)≥f(х_о)).

Точки min и max – точки экстремума. Значение ф-и в этих точках называется max (min) ф-и, экстремумом ф-и.

Необходимое условие локального экстремума диф-ой ф-и, но недостаточное: если диф-я ф-я имеет в точке х_о экстремум, то производная f’(x_o)=0.

Если расширить класс рассматриваемых ф-ий и допустить, что в отдельных точках производная равна ∞ или вовсе не сущ-ет, то экстремум может прийти на какую-либо из этих точек.

Теорема об необходимом условии локального экстремума: если ф-я f(x) имеет в точке х_о локальный экстремум, то производная в этой точке обращается в 0, ∞ или вовсе не сущ-ет (критические точки по первой производной).

14. Необходимое и достаточное условия монотонности дифференцируемых функций с геометрической интерпретацией. нахождение интервалов монотонности функции.

Если производная ф-и f(x) положительна (отрицательна) во всех точках промежутка, то ф-я f(x) монотонно возрастает (убывает) на этом промежутке.

Ф -я f(x) называется возрастающей (убывающей) на промежутке, если для любых двух точек x1 и x2 (x1 меньше x2) этого промежутка справедливо неравенство: f(x1)<f(x2) (f(x1)>f(x2)).

Необходимое условие возр (убыв) ф-и: если диф-мая ф-я y=f(x) возр (убыв) на интервале (a,b), то в любой точке х этого интервала f’(x)≥0 (f’(x)≤0).

Геометрически это означает, что в каждой точке графика возраст ф-и касательная или образует острый угол с осью Ox или параллельная с ней, а в каждой точке графика убывающей ф-и касательная или образует тупой угол с осью Ox или параллельна с ней.

Например, ф-я у=х³ – возрастающая. (f’(0)=0)

Достаточное условие: Если производная диф-ой ф-и положительна (отрицательна) повсюду (т.е. ф-я непрерывно возрастает или убывает повсюду), исключая лишь разве конечное число х, ф-я будет возрастать (убывать). Разделить интервалы непрерывности могут лишь точки, в которых f’(x)=0.

Точка, в которой производная обращается в ноль называется стационарной. Но не каждая стац точка может разделять интервалы монотонности.

Пример. f(x)=x², f’(0)=0, x=0 стац точка

Пример. f(x)=|x|, но f’(0) не существует