15*. Необходимые и достаточные условия экстремума функции с геометрической интерпретацией и конкретынми примерами.
Пусть ф-я f(x) определена и непрерывна на некотором интервале (a,b), Содержащем точку x0. x0 называют точкой max (min) ф-ии f(x), если существует такая δ-окрестность точки x0 , что для всех x≠x0 этой окрестности выполняется нер-во f(x)≤f(xo) (f(x) ≥f(xo))/ Точки min и max- т. экстемума.
Значение ф-ии в этих точках- min(max) ф-ии (экстремум ф-ии).
Необходимое условие локального экстремума:
Если деф-я ф-я имеет в т.xo локальный экстремум , то производнаяа в этой точке f'(xo)=0, ∞ или вовсе не существует.(Критические точки по 1ой производной)
{Если допустить, что в отдельных точках производная равна ∞ или вовсе не существует, то экстремум может прийти на какую-либо из этих точек.}
Достаточное условие:
1.Пусть x0-критическая точка ф-ии f(x),если при переходе через точку xo слева направо производная f'(x) меняет знак с + на – (с - на+), то ф-я f(x) в точке x0 имеет локальный max(min). Если ф-я не меняет знака в δ-окестности т. x0, то данная ф-я не имеет в этой точке локального экстремума.
2.Если первая производная дважды диф. Ф-ии =0 в нек. т. x0, а 2ая производная в этой же точке положительна (отрицательна), то x0- точка локального min(max).
f'’(x0)>0 x0 – т.min, f'’(x0)<0 x0 – т.max
3. Предположим, что ф-я f(x) в некоторой окрестности т. x0 n раз непрерывно дифференцируема, те имеет непрерывные производные до n-ого порядка включительно.
Пусть все ф-ии f'(x0)= f’’(x0)=…=f(n-1)( x0)=0, а fn( x0)≠0. Если n-нечетное, то в точке x0 экстремума нет, если n-четное, то x0 – точка экстремума, причем точка max, если fn( x0)<0, min, если fn( x0)>0.
Для нахождения наибольшего или наименьшего значения f(x) на отрезка [a,b] нужно из значения ф-ии на границах отрезка и в критических точках, принадлежащих этому отрезку, выбрать наибольшее и наименьшее.
16. Необходимое и достаточное условия выпуклости (вогнутости) графика функции. Точки перегиба и геометрический смысл перегиба. Схема нахождения точек перегиба с демонстрацией на конкретных примерах.
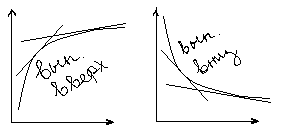
Кривая называется выпуклой вверх (вниз) на интервале (a,b), если на этом интервале кривая расположена не выше (не ниже) касательной к графику ф-и, проведенной в любой точке этого интервала.
Достаточное условие выпуклости: если вторая производная f’’(x) ф-и f(x) положительна (отрицательна) на промежутке Х, то ф-я явл выпуклой вниз (вверх) на этом промежутке.
Т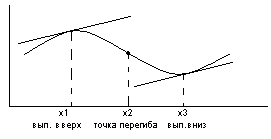
очки,
разделяющие интервалы выпуклости,
называются точками
перегиба.
Необходимое условие точек перегиба, но недостаточное: если f(x) дважды непрерывно диф-ая ф-я на некотором промежутке, то в точках перегиба кривой у=f(x), лежащих на этом промежутке f’’(x)=0.
Например, f(x)=x3, f’’(0)=0
Достаточное условие: если в некоторой окрестности точки хо f’’(x) непрерывна всюду, кроме быть может самой этой точки (в ней f’’(x) может и не сущ-ть) и при переходе через эту точку f’’(x) меняет знак, то в точке хо график ф-и имеет перегиб.
Схема исследования ф-и на выпуклость и точки перегиба:
найти f’’(x)
найти точки, в которых f’’(x)=0 или не сущ-ет
исследовать знак f’’(x) слева и справа от каждой из найденных точек, сделать вывод об интервалах выпуклости, наличии точек перегиба
найти значения ф-и в точках перегиба.
Например.