6.1.2. Передача ключей с использованием асимметричного шифрования

Рассмотрим варианты использования асимметричного шифрования для передачи секретных ключей симметричных криптосистем.

Протоколы без использования цифровой подписи.

Для передачи ключа k можно использовать следующий одношаговый протокол:

А→В: Е_kB(k,t,А),

где Е — алгоритм шифрования с открытым ключом, t — метка времени, вставляемая для предотвращения возможности повторного использования ключа.

Для осуществления взаимной аутентификации и подтверждения правильности получения ключа можно воспользоваться протоколом из [Nee78]:

1. A→В: Е_B(k₁,А),

2. В→А: Е_А(k₁,k₂),

3. А→В: Е_B(k₂).

Производя расшифрование полученных сообщений на втором и третьем шагах, стороны убеждаются в том, что они имеют дело именно с нужной стороной и что другая сторона правильно расшифровала полученное значение ключа.

Протоколы с использованием цифровой подписи.

При использовании цифровой подписи аутентифицированный протокол передачи ключей может содержать только одно сообщение и иметь, например, один из следующих трех видов:

А→В: E_B(k,t,S_A(B,k,t))

(шифрование подписанного ключа);

А→В: E_B(k,t,),S_A(B,k,t)

(зашифрование и подпись ключа);

А→В: t,E_B(A,k),S_A(B,t,E_B(A,k))

(подпись зашифрованного ключа).

Сертификаты открытых ключей

Как правило, при использовании открытых ключей хранят не сами ключи, а их сертификаты. Сертификат представляет собой набор данных

C_A=(A,k_A,t,S_kTA(A,k_A,t)),

состоящий из идентификатора абонента А, его открытого ключа k_А и, быть может, еще какой-либо дополнительной информации, например, времени t выдачи сертификата и срока его действия, заверенных цифровой подписью доверенного центра ТА или заслуживающего доверия лица. Сертификат предназначен для исключения возможности подмены открытого ключа при его хранении или пересылке.

Получив такой сертификат и проверив цифровую подпись, можно убедиться в том, что открытый ключ действительно принадлежит данному абоненту.

Международный стандарт CCITT X.509 определяет следующий протокол аутентификации с одновременным распределением ключей:

1. A→B:C_a,D_a,S_a(D_a),

2. В→А: C_B,D_B,S_B(D_B),

3. A→B:r_B,B,S_A(r_B,B),

где С_А и С_B — сертификаты сторон, S_A и S_B — цифровые подписи сторон,

D_A = (t_А ,r_A,B, data₁, Е_B (k₁)),

D_В = (t_В, r_B, A,r_A, data₂,Е_А (k₂))

- наборы передаваемых и подписываемых данных. В поля data заносится дополнительная информация для аутентификации источника. Третий шаг протокола требуется стороне В для подтверждения того, что она действительно взаимодействует со стороной А.

6.1.3. Открытое распределение ключей

Открытое распределение ключей позволяет двум абонентам выработать общий секретный ключ путем динамического взаимодействия на основе обмена открытыми сообщениями без какой-либо общей секретной информации, распределяемой заранее. Важным преимуществом открытого распределения является также то, что ни один из абонентов заранее не может определить значения ключа, так как ключ зависит от сообщений, передаваемых в процессе обмена.

Первый алгоритм открытого распределения ключей был предложен У. Диффи и М. Хеллманом. Для его выполнения стороны должны договориться о значениях большого простого числа р и образующего элемента α мультипликативной группы 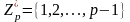. Для выработки общего ключа k они должны сгенерировать случайные числа х, 1≤ х ≤ р - 2, и у, 1 ≤ у ≤ р - 1, соответственно. Затем они должны обменяться сообщениями в соответствии с протоколом:

1. А→В: α ^х mod p,

2. В→А: α ^y mod p.

Искомый общий ключ теперь вычисляется по формуле:

k = (α ^у)^х = (α ^х)^у mod p.

Недостатком этого протокола является возможность атаки типа "злоумышленник в середине", состоящей в следующем. Предположим, что злоумышленник имеет возможность осуществлять подмену передаваемых абонентами сообщений.

Рассмотрим два протокола, устраняющие этот недостаток. Первый протокол, называемый STS (station-to-station), предполагает, что пользователи применяют цифровую подпись, которой подписываются передаваемые по протоколу Диффи—Хеллмана сообщения:

1. А →В: α ^х mod p,

2. В→А: α ^y mod p, E_k(S_B(α ^y, α ^x)),

3. A→B: E_k(S_A(α ^x, α ^y)).

Здесь S_A и S_B — цифровые подписи пользователей А и В соответственно, k — искомый общий ключ. Они позволяют гарантировать достоверность получения сообщения именно от того пользователя, от которого это сообщение получено. Шифрование значений подписей пользователей введено для того, чтобы обеспечить взаимное подтверждение правильности вычисления значения ключа.

Еще один подход также предполагает наличие у абонентов открытых ключей, но вместо цифровой подписи предлагается использовать модифицированную процедуру выработки общего ключа. Рассмотрим протокол MTI (Мацумото-Такашима-Имаи).

Предположим, что пользователи А и В имеют секретные ключи а, 1 ≤ а ≤ р - 2, и b, 1≤ b ≤ р - 2 , соответственно, и публикуют свои открытые ключи z_A = α^a mod p и z_B = α^b mod p. Для выработки общего секретного ключа k они должны сгенерировать случайные числа х, 1≤ х ≤ р - 2, и у, 1≤ у ≤ р - 2, соответственно, а затем обменяться следующими сообщениями:

1. А→В: α^х mod p,

2. В→А: α^y mod p.

Искомый общий ключ вычисляется по формуле:

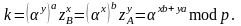
Теперь любая подмена сообщений приведет к тому, что все стороны получат различные значения ключа, что, в свою очередь, приведет к невозможности чтения всей передаваемой информации.