4.2. Примеры современных асимметричных шифров
4.2.1. Криптосистема rsa
Система построена на следующих функциях:
Односторонняя функция - умножение двух больших простых чисел:
N = p · q.
Обратная задача – задача факторизации, является сложной.
Односторонняя функция с секретом - потенцирование (возведение в степень) по модулю составного N = p · q с фиксированной степенью E:
C = mE mod N.
Обратная задача – задача извлечения корня степени E по модулю N:
является сложной, если неизвестно разложение N на множители (секрет) и является простой при известном разложении N.
В дальнейшем секретные элементы криптосистем обозначаются строчными (p, q, m и пр.) открытые прописными (N, C, E и пр.) латинскими буквами.
Предположим абонент A считает нужным разрешить всем желающим отправлять ему секретные сообщения, расшифровать которые способен только он. Для этого выбирается два больших простых числа p и q, которые держатся в секрете, и публикуется их произведение
N = p · q,
которое называют модулем алгоритма. Кроме того, выбирается шифрующая экспонента E, удовлетворяющая условию
НОД (E, (p – 1), (q – 1)) = 1.
Как правило E берут равным 3, 17 или 65537. Пара, доступная всем желающим, - это (N, E). Для выбора секретного ключа применяют расширенный алгоритм Евклида к паре чисел E и
(p – 1)(q – 1), получая при этом расшифровывающую экспоненту d. Найденная экспонента удовлетворяет соотношению
E · d = 1 (mod (p – 1)(q – 1)) = 1.
Секретным ключом является тройка (d, p, q). Фактически, можно было бы выбросить простые делители p и q из ключа и помнить лишь о d и всем числе N. Но, как будет рассмотрено позднее, это снизит скорость алгоритма.
Допустим теперь пользователь B намерен зашифровать сообщение, адресованное A. Он сверяется с открытым ключом и представляет сообщение в виде числа m, строго меньшего модуля N алгоритма. Шифртекст C получается из m по следующему правилу:
C = mE (mod N).
A, получив шифрограмму, расшифровывает ее, возводя число C в степень d:
m = Cd (mod N).
Равенство имеет место в связи с тем, что порядок группы
#(Z/NZ)* = φ(N) = (p – 1)(q – 1).
Потому по теореме Лагранжа (Эйлера-Ферма),
x(p - 1)(q - 1) = 1 (mod N)
для любого числа x (Z/NZ)*. Поскольку E и d взаимно обратны по модулю (p – 1)(q – 1), при некотором целом числе s получается равенство
Ed – s(p – 1)(q – 1) = 1.
Следовательно,
Cd = (mE)d = mEd = m1 + s(p – 1)(q – 1) = m · m s(p – 1)(q – 1) = m (mod N).
Пример. Пусть p = 7 и q = 11. Тогда N = 77, а (p – 1)(q – 1) = 6 · 10 = 60. В качестве открытой шифрующей экспоненты возьмем число E = 37, поскольку НОД(37, 60) = 1. Применяя расширенный алгоритм Евклида, найдем d = 13, так как
37 · 13 = 481 = 1 (mod 60).
Для зашифрования сообщения численное представление которого имеет вид m = 2:
C = mE (mod N) = 237 (mod 77) = 51.
Расшифрование происходит аналогично:
m = Cd (mod N) = 5113 (mod 77) = 2.
4.2.2. Взаимосвязь компонентов rsa
Задача RSA: Даны числа C и E, последнее из которых удовлетворяет соотношению:
НОД(E, (p – 1)(q – 1)) = 1.
Требуется найти такое число m, что
mE = C (mod N).
Лемма. Задача RSA не сложнее проблемы факторизации.
Доказательство. Применяя алгоритм факторизации, разложим число N на простые множители, вычислим значение функции Эйлера Ф = (N) и найдем
D = 1/E (mod Ф).
Теперь, зная число D, легко восстановить m, поскольку
CD = mED = m1 (mod Ф) = m (mod N).
Отсюда следует, что при известных p и q легко находятся d и m.
Самые большие числа, которые к настоящему времени удается разложить на множители за разумное время, имеют 500 двоичных знаков. В связи с этим, для обеспечения стойкости систем среднего срока действия, рекомендуют брать модули шифрования порядка 1024 бит. Для систем большого срока действия следует выбирать модули, состоящие из 2048 бит.
Секретная экспонента и проблема факторизации:
Лемма. Если известна секретная экспонента d алгоритма RSA, соответствующая открытому ключу (N, E), то число N можно эффективно разложить на множители.
Доказательство. При некотором целом s имеет место равенство
Ed – s(p – 1)(q – 1) = 1.
Возьмем произвольное целое число X 0. Тогда
XEd – 1= 1(mod N).
Вычисляем квадратный корень Y1 по модулю N:
что можно сделать, поскольку Ed – 1 известно и четно. Приходим к тождеству
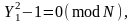
которое можно использовать для определения делителей числа N с помощью вычисления НОД(Y1 – 1, N). Однако это будет работать только если Y1 1 (mod N).
Предположим, что нам не повезло и Y1 = 1 (mod N). Если Y1 = –1 (mod N), вернемся к началу и выберем другое число X. Если Y1 = 1 (mod N), то можно взять еще один квадратный корень
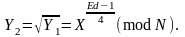
Опять получаем
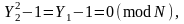
откуда НОД(Y2 – 1, N) – делитель числа N. К сожалению, здесь тоже может оказаться, что Y2 = 1 (mod N). Тогда придется повторить все снова.
Алгоритм необходимо повторять до тех пор, пока мы не разложим N на множители и не придем к числу (ED – 1)/2t, которое уже не будет делиться на 2. В последнем случае придется вернуться к началу алгоритма, выбрать новое случайное значение X и все повторить.
Отсюда следует, что при известном d легко найти p и q.
Алгоритм, приведенный в доказательстве, - типичный пример алгоритма Лас-Вегаса, вероятностного по своей природе, которая проявляется в процессе работы. Но если уж ответ отыщется, то он будет обязательно верным.
Пример. Входные данные задачи RSA:
N = 1441499, E = 17 и d = 507905.
Напомним, что мы предполагаем известной расшифровывающую экспоненту d, которая обычно хранится в секрете. Опираясь на предыдущий алгоритм, найдем числа N. Положим
T1 = (Ed – 1)/2 = 4317192,
X = 2.
Для вычисления Y1, сделаем преобразования :
Поскольку Y1 оказался равным 1, нам нужно взять
T2
= T1/2
= (Ed
– 1)/4
= 2158596
и
.
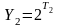Теперь
Снова нужно повторять предыдущие шаги, что приведет нас к
T3 = (Ed – 1)/8 = 1079298
и
Отсюда
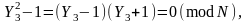
и мы можем найти простой делитель числа N, вычислив
НОД(Y3 – 1, N) = 1423.
Значение функции Эйлера (N) и проблема факторизации:
Лемма. Значение Ф = (N) позволяет эффективно разложить число N на множители.
Доказательство. Имеем
Ф = (p – 1)(q – 1) = N – (p + q) + 1.
Следовательно, положив S = N + 1 – Ф, мы получим
S = p + q.
Нам нужно определить числа p или q, опираясь на их сумму S и произведение N. Рассмотрим многочлен
f(X) = (X – p)(X – q) = X2 – SX + N.
Теперь можно найти как p, так и q, решая квадратное уравнение f(X) = 0 стандартным образом:
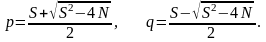
Отсюда следует, что при известном (N) легко найти p и q.
Пример. Открытый модуль N = 18923 криптосистемы RSA. Известно Ф = (N) = 18648. Вычисляем
S = p + q = N + 1 – Ф = 276.
Соответствующий многочлен имеет вид:
f(X) = X2 – SX + N = X2 – 276X + 18923,
а его корни – p = 149, q = 127.