4.2.4. Криптосистема Рабина

Система базируется на трудности задачи факторизации больших целых чисел, а точнее на трудности извлечения квадратного корня по модулю составного числа N = p · q.

Эти задачи эквивалентны:

- зная простые делители числа N, можно легко извлекать корни по модулю N,

- умея извлекать корни по модулю N, можно легко разложить N на составные множители.

Такую систему можно считать в некотором отношении более криптостойкой, чем RSA. Процесс шифрования в системе Рабина происходит намного быстрее, чем практически в любой другой криптосистеме с открытым ключом. Однако, несмотря на эти преимущества, система Рабина используется все же реже, чем RSA.

Выбираются два простых числа p и q, удовлетворяющие условию

p = q = 3 (mod 4).

Такой специальный вид чисел сильно ускоряет процедуру извлечения корней по модулю p и q. Закрытым ключом системы является пара

(p, q).

Для определения соответствующего открытого ключа берут произведение N = p · q и генерируют случайное целое число B  {0, …, N – 1}. Открытый ключ это пара

(N, B).

Для шифрования сообщения m в алгоритме Рабина вычисляют

C = m(m + B) (mod N).

Таким образом, шифрование состоит из операции сложения и умножения по модулю N, что обеспечивает более высокую скорость шифрования, чем в RSA, даже если в последней выбирают небольшую шифрующую экспоненту.

Расшифрование в этом алгоритме гораздо более сложное. По существу нужно вычислить

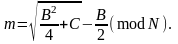
На первый взгляд, здесь не требуется никакой секретной информации, но, очевидно, для извлечения корней по модулю N очень и очень полезно знать разложение N на простые множители. Поскольку N – произведение двух простых чисел, существует четыре возможных квадратных корня из числа по модулю N. Поэтому при расшифровании получается четыре возможных варианта открытого текста. Чтобы выбор был более определенным, стоит к открытому тексту добавлять некую избыточную информацию.

Объясним, почему при расшифровании мы действительно получаем m. Напомним, что шифртекст имеет вид

C = m(m + B) (mod N).

поэтому

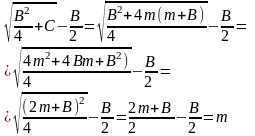
Конечно предполагаем, что мы выбрали правильный корень из четырех.

Пример. Открытый и закрытый ключи имеют вид:

- p = 127, q = 131,

- N = 16637 и B = 12345.

Для шифрования сообщения m = 4410 вычисляем

C = m(m + B) (mod N) = 4633.

При обратной операции сначала находим

T = B²/4 + C (mod N) = 1500,

а затем извлекаем квадратные корни из T по модулю p и q:

После этого, применяя китайскую теорему об остатках к паре

22 (mod p) и 37 (mod q),

находим квадратный корень из T по модулю N:

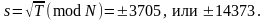
Четыре варианта расшифрования

4410, 5851, 15078, или 16519

получаются из формулы

.

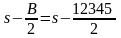4.2.5. Рюкзачные криптосистемы

Задача об укладке рюкзака. Задано множество {v_i} из k натуральных чисел и целое число S.

Требуется найти такое k-разрядное число n = (n_{k – 1}n_{k – 2}…n₁n₀)₂ (где n_i  {0, 1} суть значения разрядов в двоичной записи чиcла n), что 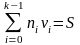, если такое n существует.

В зависимости от набора {v_i} и числа S, такого решения может не быть вообще, решений может быть несколько или решение будет единственным. Такая задача является сложной.

Частный случай – задача об укладке быстровозрастающего рюкзака. Это случай, когда величины v_i, будучи упорядочены в порядке возрастания, обладают тем свойством, что каждое число больше суммы всех предыдущих.

Такая задача имеет эффективный алгоритм решения:

1. Положим W = S и j = k.

2. Начиная с n_{j – 1} и последовательно уменьшая j, полагаем все n_j = 0 до тех пор, пока не придем к первому такому значению j (обозначим его через i₀), что 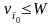. Положим

3. Заменим W на 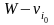, положим j = i₀ и, если W > 0, то переходим к шагу 2.

4. Если W = 0, то цель достигнута. Если W > 0 и все оставшиеся v_i больше W, то ясно, что решения n = (n_{k – 1}n_{k – 2}…n₁n₀)₂ задачи не существует. Если решение есть, то оно единственное.

Пример. Набор {2, 3, 7, 15, 31} является быстрорастущим набором, а S = 24. Тогда проходя пятерку значений справа налево, мы видим, что n₄ = 0 (31 > 24), n₃ = 1 (15 < 24 и в этот момент заменяем 24 на 24 – 15 = 9), n₂ = 1 (7 < 9 и в этот момент заменяем 9 на 9 – 7 = 2), n₁ = 0 (3 > 2), n₀ = 1 (2 = 2). Таким образом, получаем n = (01101)₂ = 13.

Криптосистема Меркля-Хеллмана

Предположим, что элементы открытого текста имеют в качестве своих числовых эквивалентов k-разрядные двоичные числа n.

Каждый пользователь выбирает быстрорастущий набор {v₀, …, v_{k – 1}}, целое число 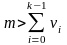и целое число a, такое что a < 0 < m и НОД(a, m) = 1.

После этого вычисляются b = a ^-1 (mod m) и k-элементный набор {W_i} = {W₀, …, W_{k –1}}, пределяемый равенствами W_i = av_i (mod m). Пользователь держит числа {v_i}, m, a и b в секрете, а набор {W_i} делает общеизвестным. Таким образом, ключом зашифрования является набор

{W₀, …, W_{k –1}},

а ключом расшифрования – пара

(b, m),

которая вместе с ключом зашифрования позволяет определить набор {v₀, …, v_{k – 1}}.

Желающий передать сообщение n = (n₀ … n_{k – 1})₂ пользователю с ключом шифрования {W_i} вычисляет

и передает это число.

Чтобы прочесть это сообщение, пользователь сначала находит s = bC:

,

поскольку bW_i ≡ bav_i ≡ v_i (mod m). Теперь можно воспользоваться приведенным выше алгоритмом для быстровозрастающего рюкзака и найти единственное решение

(n₀ … n_{k – 1})₂ = n задачи о подмножестве {v_i} с суммой равной s.

Пример. Элементы открытого текста – двоичные представления букв 26-буквенного алфавита от «A» = 0 = (00000)₂ до «Z» = 25 = (11001)₂ .

Cекретный быстровозрастающий набор {v₀, …, v_{k – 1}} = {2, 3, 7, 15, 31}.

Выберем m = 61, a = 17, тогда b = 18 и открытый ключ шифрования

{W₀, …, W_{k –1}} = {34, 51, 58, 11, 39}.

Чтобы послать сообщение «WHY» корреспондент должен вычислить:

«W» = (10110)₂  51 + 58 + 39 = 148,

«H» = (00111)₂  34 + 51 + 58 = 143,

«Y» = (11000)₂  11 + 39 = 50.

N = n₁, n₂, n₃ = 148, 143, 50.

Чтобы прочитать сообщение N, сначала умножают эти числа на 18 и приводят результаты по модулю 61, получают S = s₁, s₂, s₃ = 41, 12, 46 далее, пользуясь алгоритмом для быстрорастущего рюкзака для всех s_i, восстанавливают сообщение

(10110)₂, (00111)₂, (11000)₂