4.1.6. Китайская теорема об остатках

Для двух cравнений.

Система cравнений

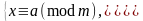
при НОД(m, n) = 1 имеет единственное решение по модулю m · n, которое определяется по формулам:

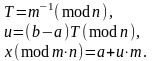
Пример.

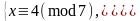
T = 7^-1(mod 5) = 2^-1 (mod 5) = 3 (mod 5),

u = (3 – 4) · 3 (mod 5) = 4 · 3 (mod 5) = 2 (mod 5),

x (mod 35) = 4 + 2 · 7 = 18.

Общий случай КТО.

Пусть m₁, ..., m_r и a₁, ..., a_r – целые числа, причем все m_i попарно взаимно просты.

Нужно найти такой x по модулю M = m₁·m₂·...·m_r, что

x = a_i (mod m_i) для всех i.

Решение единственно и равно:

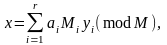
где .

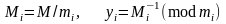Пример.

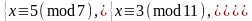
M₁ = 143, y₁ = 5,

M₂ = 91, y₂ = 4,

M₃ = 77, y₃ = 12.

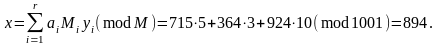
4.1.7. Символы Лежандра и Якоби. Извлечение корней

Пусть p – простое число, большее 2. Рассмотрим отображение

,

сопоставляющее каждому элементу поля его квадрат. На множестве ненулевых элементов поля F_p это отображение в точности «два-в-один», то есть если из ненулевого элемента x  F_p можно извлечь квадратный корень, то таких корней у него ровно 2 и, кроме того, ровно половина элементов из являются полными квадратами. Полные квадраты в называются квадратичными вычетами по модулю p. Множество всех квадратичных вычетов по модулю p является подгруппой порядка (p – 1)/2 в мультипликативной группе . Элементы мультипликативной группы из которых нельзя извлечь квадратный корень, называются квадратичными невычетами.

Для выявления полных квадратов по модулю p вводится символ Лежандра

Он равен 0, если a делится на p, +1, если a – квадратичный вычет по модулю p, и – 1, если a – квадратичный невычет.

Символ Лежандра легко вычисляется по формуле

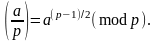
Но использование этой формулы сопряжено с вычислениями больших степеней и на практике предпочитают пользоваться законом квадратичной взаимности

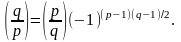
Иначе говоря

При вычислении символа Лежандра большую помощь оказывают следующие дополнительные формулы:

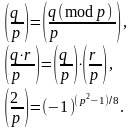
Пример. С использованием разложения на множители вычислим символ Лежандра.

Извлечение квадратного корня из квадратичного вычета a по модулю p при помощи алгоритма Шенкса.

1. Выбрать наугад такое n, что

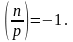
2. Пусть e, q – целые числа с нечетным q, удовлетворяющие соотношению p – 1 = 2^eq.

3. Положим y = n^q (mod p), r = e, x = a^{(q – 1)/2} (mod p).

4. Положим b = ax² (mod p), x = ax (mod p).

5. Пока b  1 (mod p) делать:

• найти наименьшее число m, такое, что

• положить

• положить

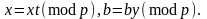
6. Вывести x.

Если p = 3 (mod 4), то для извлечения квадратного корня из a можно использовать формулу

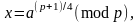
формула дает правильный ответ потому, что

.

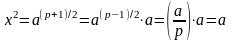Символ Лежандра определен только в случае простого знаменателя. Если же знаменатель составной, то вводится символ Якоби, обобщающий символ Лежандра.

Пусть n – нечетное число, большее 2 и

.

Символ Якоби определяется через символы Лежандра простых делителей числа n следующим образом

Символ Якоби можно вычислять так же, как и символ Лежандра, опираясь на тождество, выведенное из закона квадратичной взаимности:

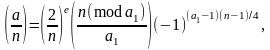
где a = 2^ea₁ и a₁ нечетно. Полезно помнить еще несколько формул, справедливых при нечетном n:

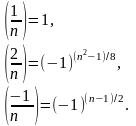
Это дает быстрый алгоритм вычисления символа Якоби и, соответственно, символа Лежандра, как его частный случай, без разложения на множители. Единственное, что нужно сделать – выделить максимальную степень двойки.

Пример.

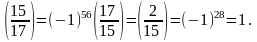
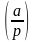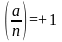Символ Лежандра сообщает нам, является ли a полным квадратом по модулю простого числа p. Символ Якоби ничего не утверждает о возможности извлечения квадратного корня из a по модулю составного числа n. Если a в действительности квадрат по модулю n, то символ Якоби будет равен +1. Однако из равенства нельзя сделать вывод о том, что a – полный квадрат. Не смотря на благоприятное равенство, квадратный корень из a может не извлекаться.

Извлечение корня из числа по модулю составного n = p · q в предположении, что разложение n на простые множители известно и a – полный квадрат по модулю n, то есть

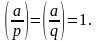
Сначала извлекается корень из a по модулю p и обозначается через s_p (таких корней два, как будет показано позже). Затем извлекается квадратный корень из a по модулю q и обозначается s_q (таких корней также два). Наконец, для вычисления искомого корня применяем китайскую теорему об остатках к системе

Пример. Вычислим корень из a = 217 по модулю n = 221 = 13 · 17.

Квадратные корни из a по модулям 13 и 17 соответственно равны s₁₃ = 3 и s₁₇ = 8. Опираясь на китайскую теорему об остатках, получаем s = 42. Проверим правильность данного решения: s² = 42² ≡ 217 (mod 221).

Существуют еще три квадратных корня из a = 217 по модулю n = 221, поскольку n имеет два простых делителя. Для их отыскания применим КТО к трем системам с коэффициентами:

s₁₃ = 10, s₁₇ = 8;

s₁₃ = 3, s₁₇ = 9;

s₁₃ = 10, s₁₇ = 9

и получить полный ответ: 42, 94, 127, 179.