4.1.2. Функция Эйлера. Поле. Теоремы Эйлера - Лагранжа и Ферма

Одна из центральных задач арифметики остатков - решение сравнения:

a · x  b (mod n)

- Если НОД (a, n) = 1, то существует ровно одно решение, и оно находится с помощью a^-1: так как

a · a^-1  1 (mod n),

то, домножив обе части сравнения на a^-1, получим

x  b · a^-1 (mod n).

- Если НОД (a, n) = g  1 и g | b, то сравнение имеет g решений. Чтобы их найти нужно разделить исходное сравнение на g:

a’ · x’  b’ (mod n’),

где a’ = a / g, b’ = b / g, n’ = n / g. Если x’ – решение полученного сравнения, то решение исходного сравнения - любое число вида

x = x’ + i · n’,

где i = 0, 1, ..., g – 1.

- В других случаях решений нет.

Пример:

7 · x  3 (mod 143) – одно решение,

11 · x  3 (mod 143) – решений нет,

11 · x  22 (mod 143) – 11 решений.

Ситуация с единственным решением наиболее интересна для криптологии, поэтому важно знать количество элементов кольца, взаимно простых с его модулем. Оно дается функцией Эйлера  и равно (n). Значение (n) можно легко найти по разложению числа n на простые множители. Если

,

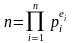где p_i – различные простые числа, то

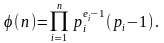
Функция Эйлера для любого n > 2 имеет четное значение.

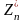- наибольшее подмножество элементов, образующих группу по умножению # = (n). (количество элементов мультипликативной группы кольца вычетов по модулю n равно (n)).

Особый интерес представляют частные случаи:

1. Если p простое, то (p) = p – 1.

2. Если p и q – простые и p  q, то (p · q) = (p – 1)(q – 1).

Если p - простое число, то любой элемент в Z_p (или Z/pZ) обладает мультипликативным обратным. Кольца с такими свойствами называются полями.

Определение. Полем называется множество (F, ·, +) с двумя операциями, обладающее свойствами:

- (F, +) – абелева группа с нейтральным элементом 0,

- (F \ {0}, ·) – абелева группа с нейтральным элементом 1,

- (F, ·, +) удовлетворяет закону дистрибутивности (умножение дистрибутивно относительно сложения).

Поле – коммутативное кольцо, в котором каждый ненулевой элемент обратим. Каждый ненулевой элемент кольца Z_p взаимно прост с p, так как p простое и, следовательно, обратим. Значит Z_p – конечное поле, которое обычно называют полем вычетов по модулю p и обозначают F_p = {0, 1, ..., p – 1}. Мультипликативная группа = {1, ..., p – 1} поля вычетов содержит все ненулевые элементы F_p.

Теорема Лагранжа. .

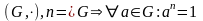Обобщение Эйлера для малой теоремы Ферма. 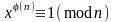, при НОД(x, n) = 1.

Малая теорема Ферма. .

4.1.3. Конечные поля

Целые числа по простому модулю – не единственный пример конечных полей. Более общий тип полей используется при рассмотрении таких криптосистем как AES, поточных шифров на основе РСЛОС и криптосистем, на основе эллиптических кривых.

Рассмотрим множество многочленов от переменной x с коэффициентами из F_p. Это множество обозначается через F_p[x] и образует кольцо относительно естественных операций суммы и умножения многочленов. Особый интерес представляет случай p = 2.

Пример. В кольце F₂[x] выполнены равенства:

Зафиксируем многочлен f(x) и будем рассматривать остальные элементы кольца F_p[x] по модулю f(x). Как и натуральные числа по модулю n, возможные остатки от деления на многочлен f(x), будут образовывать кольцо. Оно обозначается через F_p[x]/f(x)F_p[x] (по аналогии с Z/nZ).

Пример. f(x) = x⁴ + 1 и p = 2. Тогда

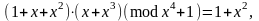
так как

По аналогии с целыми числами по модулю n, где рассматривалось сравнение

a · x  b (mod n)

можно поставить аналогичный вопрос и для многочленов. Пусть a, b и f – многочлены из F_p[x]. Существование решения уравнения

a ·   b (mod f)

также зависит от НОД (a, f) и также возможны три ситуации. Наиболее интересна ситуация, когда НОД (a, f) = 1.

Многочлен называется неприводимым, если у него нет делителей, отличных от него самого и констант. Неприводимость многочленов - то же самое, что и простота целых чисел. Кольцо F_p[x]/f(x)F_p[x] является конечным полем тогда и только тогда, когда многочлен f(x) неприводим.

Рассмотрим два неприводимых многочлена над полем F₂

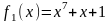и .

Возникают два конечных поля

F₁ = F_p[x]/f₁(x)F_p[x] и F₂ = F_p[x]/f₂(x)F_p[x],

каждое состоит из 2⁷ двоичных многочленов (каждый имеет ровно 7 коэффициентов равных 1 или 0), степень которых не превосходит 6. Сложение в обоих полях выглядит одинаково, поскольку при вычислении суммы складываются коэффициенты многочленов по модулю 2. А вот умножаются элементы этих полей по разному:

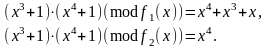
Действительно ли различны поля F₁ и F₂ или это только кажущееся различие?

Изоморфны ли поля F₁ и F₂?

Изоморфизм: отображение : F₁  F₂, удовлетворяющее двум требованиям:

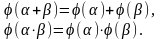
Для построения изоморфизма между F₁ и F₂ достаточно показать как выражается корень f₂(x) в виде многочлена от корня f₁(x).

Изоморфизм существует между любыми двумя конечными полями с одинаковым числом элементов. Все конечные поля совпадают либо с целыми числами по простому модулю, либо с многочленами по модулю неприводимого многочлена.

Теорема. Существует единственное (с точностью до изоморфизма) конечное поле с числом элементов равным степени простого числа.

Конечное поле из q = p^d элементов обозначается символом F_q или GF(q) (поле Галуа из q элементов).

Любое конечное поле K содержит в себе экземпляр поля целых чисел по некоторому простому модулю p, который называется простым подполем поля K. Число элементов простого подполя называется характеристикой поля и обозначается через char K. В частности char F_p = p. На конечном поле характеристики p можно определить отображение Фробениуса:

Ф: F_q  F_q, Ф() = (^p)

которое является автоморфизмом (изоморфизмом поля с самим собой). Множество элементов из F_q, остающихся неподвижными при действии Ф, совпадает с его простым подполем:

{  F_q| ^p = } = F_p.

Это утверждение – обобщение малой теоремы Ферма на случай любых конечных полей.

Ненулевые элементы конечного поля составляют конечную абелеву циклическую группу 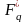. Образующая этой группы называется примитивным элементом конечного поля. Примитивный элемент есть в любом конечном поле, их может быть и несколько. Всегда можно найти такой элемент g  F_q, что любой ненулевой элемент   F_q будет представляться в виде

 = g^x

при некотором целом показателе x.

Пример. В поле из восьми многочленов

.

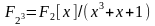В нем существует 7 ненулевых элементов, а именно

1, ,  + 1, ², ² + 1, ² + , ² +  + 1,

где  - корень многочлена x³ + x + 1 (искусственно введенный элемент, удовлетворяющий соотношению ³ +  + 1 = 0, в котором все действия выполняются по модулю 2).

Тогда:

¹ = ,

² = ²,

³ =  + 1,

⁴ = ² + ,

⁵ = ² + 1,

⁶ = ² +  + 1,

⁷ = 1

и  - примитивный элемент поля 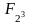. Целые числа по модулю p также имеют примитивный элемент, так как F_p – конечное поле.