3.4.3.Регистры сдвига с обратной связью

Регистр сдвига с обратной связью состоит из двух частей: регистра сдвига и функции обратной связи.

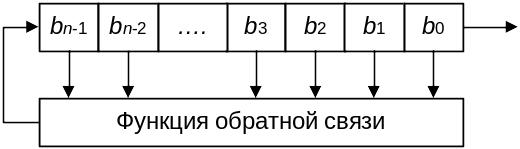
Рис 19. Регистр сдвига с обратной связью

В общем случае регистр сдвига представляет собой последовательность некоторых элементов кольца или поля. Наиболее часто применяются битовые регистры сдвига. Длина такого регистра выражается числом битов. При каждом извлечении бита все биты регистра сдвигаются вправо на одну позицию. Новый старший бит рассчитывается как функция всех остальных битов регистра. Выходом обычно является младший значащий бит. Периодом регистра сдвига называют длину выходной последовательности до начала ее повторения.

Простейший тип регистров сдвига – регистр сдвига с линейной обратной связью (РСЛОС или ЛРС). Обратная связь – простая операция XOR над некоторыми битами регистра. Перечень этих битов определяется характеристическим многочленом и называется последовательностью отводов. Иногда такую схему называют конфигурацией Фибоначчи.

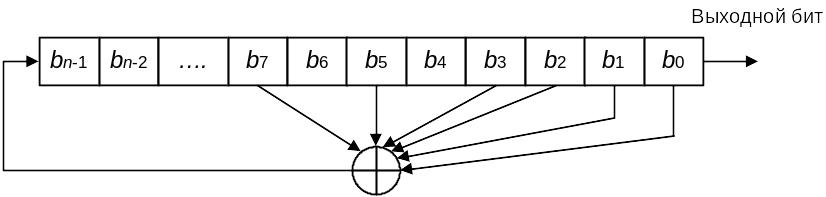
Рис.20. РСЛОС конфигурации Фибоначчи

При программной реализации РСЛОС пользуются модифицированной схемой: для генерации нового значащего бита вместо использования битов последовательности отводов над каждым ее битом выполняется операция XOR с выходом генератора, заменяя старый бит последовательности отводов. Такую модификацию иногда называют конфигурацией Галуа.

Рис.21. РСЛОС конфигурации Галуа

n-битовый РСЛОС может находиться в одном из 2ⁿ – 1 внутренних состояний. Это значит, что теоретически такой регистр может генерировать псевдослучайную последовательность с периодом 2ⁿ – 1 битов (заполнение нулями совершенно бесполезно). Прохождение всех 2ⁿ – 1 внутренних состояний возможно только при определенных последовательностях отводов. Такие регистры называют РСЛОС с максимальным периодом. Для обеспечения максимального периода РСЛОС необходимо, чтобы его характеристический многочлен был примитивным по модулю 2. Степень многочлена является длиной регистра сдвига. Примитивный многочлен степени n – это такой неприводимый многочлен, который является делителем 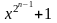, но не является делителем x^d + 1 для всех d, являющихся делителями 2ⁿ – 1. (При обсуждении многочленов термин простое число заменяется термином неприводимый многочлен). Характеристический многочлен приведенных на рисунках РСЛОС:

x³² + x⁷ + x⁵ + x³ + x² + x + 1

примитивен по модулю 2. Период такого регистра будет максимальным, циклически проходя все 2³² – 1 значений до их повторения. Наиболее часто используются прореженные многочлены, т.е. у которых есть только некоторые коэффициенты. наиболее популярны трехчлены.

Важным параметром генератора на базе РСЛОС является линейная сложность. Она определяется как длина n самого короткого РСЛОС, который может имитировать выход генератора. Линейная сложность важна, поскольку при помощи простого алгоритма Берленкемпа-Мэсси можно воссоздать такой РСЛОС, проверив всего 2n битов гаммы. С определением нужного РСЛОС поточный шифр фактически взламывается.

Помимо РСЛОС применяются и регистры сдвига с нелинейной обратной связью, обратной связью по переносу и пр.

Ряд генераторов разработан на основе теоретико-числового подхода (генераторы Блюма-Микали, RSA, BBS, сжимающие, аддитивные генераторы и пр.).

Математическое обеспечение синтеза поточных криптографических алгоритмов разработано более полно и подробно по сравнению с блочными криптоалгоритмами. Тем не менее для создания поточных шифров зачастую используют блочные криптоалгоритмы в режимах OFB или CFB.