3.6.2. Спектральная плотность
Спектр мощности содержит ту же информацию, что и автокорреляционная функция. Фактически он может быть получен как преобразование Фурье от корреляционного интеграла . Спектральная плотность определяется формулой
,
где
.
Здесь
– Фурье-амплитуда:
,
и
– отсчеты
фазовых координат.
Для дискретной системы спектр мощности определяется выражением
.
Спектр мощности есть мера количества энергии, которую данная реализация несет в каждом частотном интервале. Временные реализации, полученные из периодических (квазипериодических) траекторий, имеют спектр мощности, сконцентрированный на конечном или счетном множестве частот. Непрерывный спектр (т. е. абсолютно непрерывный относительно меры Лебега) является индикатором хаоса.
3.6.3. Связь автокорреляционной функции и спектра
Автокорреляционная функция и спектральная плотность тесно связаны между собой. Из определения спектральной плотности после несложных преобразований находим
.
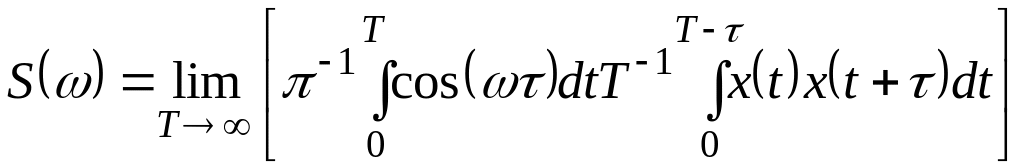Допустив, что имеется возможность перестановки порядка выполнения операций, получим
или
.
Предположим, что
–
периодическая
функция с периодом
,
тогда ее можно разложить в ряд Фурье
,
где
,
а
– коэффициенты
Фурье. В этом случае автокорреляционная
функция равна
.
Функция
– действительная,
поэтому имеет место равенство
.
Следовательно, автокорреляционная
функция также является периодической
с периодом
.
Спектральная плотность периодической функции равна
.
Таким образом,
спектр периодической функции, отвечающий
периодическому движению динамической
системы, является дискретным и будет
содержать, помимо основной частоты
,
кратные гармоники
.
Пусть
– квазипериодическая
функция
,
где
.
По каждой переменной
период равен
.
Разложим вектор
в ряд Фурье по системе базисных функций
.
Тогда для значений автокорреляционной функции и спектра квазипериодической функции имеем
,
.
Следовательно,
спектр квазипериодической функции
содержит всевозможные линейные комбинации
частот
.
Если число частот движения велико, то
линии в спектре будут расположены
достаточно плотно, однако спектр будет
оставаться дискретным.
Если динамика системы является хаотичной, то функция будет апериодической функцией времени, а спектр – сплошным (или непрерывным).
3.7. Фрактальные структуры и размерность аттрактора
Странный аттрактор – ограниченное притягивающее множество, которое одновременно является аттрактором и не является подмногообразием. Структура этих множеств весьма сложна, а топологические свойства – экзотичны. В частности, для них оказывается достаточно бесполезными обычные понятия объема (длины) или топологической размерности.
В диссипативной динамической системе фазовый объем с течением времени сокращается, фазовые кривые притягиваются к некоторому множеству (аттрактору). В случае хаотического режима фазовая траектория на аттракторе выглядит как клубок перепутанных нитей, и малое возмущение траектории может существенно изменить направление движения. Динамическая система со странным аттрактором характеризуется глобальным сжатием фазового объема и локальной неустойчивостью фазовых траекторий.