4.5.2. Вычисление вероятностных размерностей

Напомним, что в основе вероятностных размерностей лежит вычисление обобщенных энтропий

,

где  – мера ‑го кубика, покрывающего аттрактор. При основной вклад в сумму, стоящую под знаком логарифма, будут давать наиболее посещаемые кубики, а влияние редко посещаемых кубиков будет незначительным. Таким образом, одну проблему удается решить. Используя различные разбиения на кубики, можно для каждого разбиения вычислить , а затем, аналогично емкости, оценить путем линейной аппроксимации . Однако такая методика также требует больших выборок.

Сумму , называемую обобщенным корреляционным интегралом, можно представить в виде

,

т. е. как среднее (в общем случае среднее геометрическое) значение меры кубика размера . Для оценки этого среднего значения рассчитывается мера кубика или шара радиуса с центром в каждой точке , а затем усредняются полученные значения по всем таким шарам. Обозначим через число точек внутри ‑шара с центром . Его меру можно приближенно оценить как , а значение обобщенного корреляционного интеграла равно

.

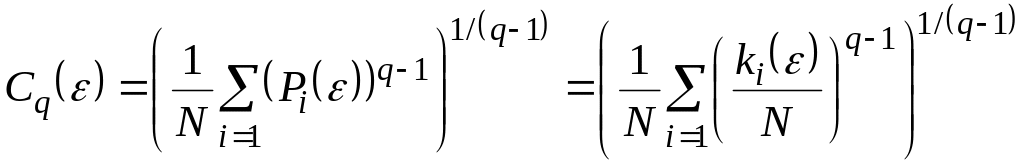В случае это соотношение существенно упрощается

,

а величину называют корреляционным интегралом. Последняя сумма – это удвоенное число пар точек, расстояние между которыми не превосходит . Таким образом, мы пришли к широко известному определению корреляционного интеграла

.

Оказалось, что для того, чтобы оценить информационную размерность по корреляционному интегралу, необходимы выборки существенно меньшей размерности, чем в предыдущих случаях. Методика оценки та же самая – линейная аппроксимация зависимости по «наиболее линейному» участку. Саму размерность называют корреляционной размерностью или корреляционным показателем.

Рассмотренный алгоритм расчета является самым популярным алгоритмом расчета по временным рядам. Платой за достоинства алгоритма является большой объем вычислений – расчет требует операций.

4.6. Корреляционный интеграл

Корреляционный интеграл, кроме расчета информационной размерности аттрактора, позволяет оценить уровень шума в системе, оценить энтропию, отличить хаотические системы от нехаотических систем.

Корреляционный интеграл можно рассчитать как для точек в исходном фазовом пространстве (по точкам ), так и для реконструированных векторов . В первом случае при благоприятных условиях можно оценить размерность исследуемой системы. Во втором случае корреляционный интеграл становится функцией не только , но и параметров реконструкции и (или и ). Зависимость от двух последних параметров и позволяет диагностировать хаотичность, уровень шума, оценить энтропию, время предсказуемости, верхний предел допустимой длины окна реконструкции .

Будем сравнивать значения корреляционного интеграла, вычисленные при различных значениях . Задержку считаем фиксированной. Если использовать евклидово расстояние

, (4.11)

то с увеличением все расстояния будут монотонно увеличиваться, а среднее квадратичное расстояние приближенно можно оценить следующим образом . Это в свою очередь приводит к тому, что одни и те же характерные участки на графике будут относиться к разным значениям . В некоторых случаях подобный сдвиг масштабов может препятствовать использованию описанных выше алгоритмов.

Если предполагается совместная обработка корреляционного интеграла для нескольких значений , то необходимо использовать коррекцию метрики – нормировать расстояние на размерность . Вместо формулы (4.11) расстояние следует вычислять по формуле

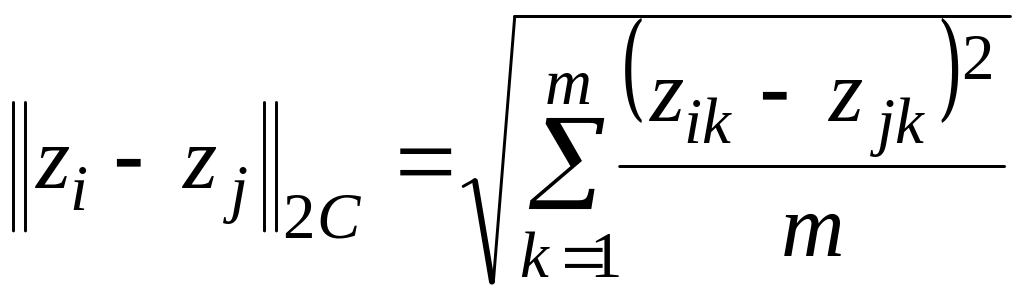. (4.12)

Метрику (4.11) иногда обозначают как или . Скорректированную метрику (4.12) обозначают как или .

При расчете корреляционного интеграла часто используют и две другие метрики

,

. (4.13)

Каждая из метрик имеет свои достоинства и недостатки. Например, и изотропны. При использовании или (когда необходимо сравнивать различные ) имеем

. (4.14)

Используя формулу (4.14), можно получить наиболее быстрые алгоритмы расчета (экономия на возведение в квадрат). Для нормы (4.13), которую называют или ‑норма, также можно построить быстрый алгоритм, кроме того, данная норма не нуждается в коррекции. Для нее, однако, интервал значений , на котором изменяется корреляционный интеграл, обычно несколько короче, что не всегда удобно.

Далее будем предполагать, что расстояние между векторами вычисляются в скорректированных нормах , или в норме . Это необходимо не для оценки размерности, а для иных, перечисленных выше, применений корреляционного интеграла.