4.3.2. Вычисление спектра по временному ряду

В ряде случаев удается определить показатели Ляпунова по временному ряду – множеству измерений состояния системы с заданным интервалом по времени. Чаще всего с разумной точностью удается вычислить только старший, наибольший показатель , реже – два старших. Большее количество удается вычислить лишь в модельных экспериментах, когда ряд порождается динамической системой малой размерности.

При исследовании траектории на аттракторе ее размерность будет совпадать с размерностью минимальной инерциальной формы , и ровно столько показателей Ляпунова, совпадающих с показателями исходной динамической системы, могут быть измерены. Остальные показателей исходной системы связаны с процессами притяжения к аттрактору и не могут быть вычислены по реконструкции траектории на аттракторе. Таким образом, по временному ряду может быть определено показателей Ляпунова не более чем , где  – динамическая размерность аттрактора.

Кроме того, для вычисления показателей Ляпунова требуются, по крайней мере, две бесконечно близкие траектории. Однако в распоряжении имеется только одна траектория. В силу свойства возвращаемости она через некоторое время оказывается в достаточно малой окрестности почти всех своих точек. Поэтому в окрестности почти каждой точки можно найти различные участки этой траектории, которые можно считать другими траекториями и использовать для оценки показателей Ляпунова.

Существующие алгоритмы оценки показателей Ляпунова по временным рядам можно разделить на два класса.

Матричные методы, связаны с восстановлением в каком-либо виде уравнений движения и аппроксимацией матрицы . Получение уравнений движения по значениям временного ряда, основанное на решении задачи идентификации динамической системы, будет представлено в пятом разделе пособия. Техника расчета самих показателей Ляпунова та же, что и для аналитически заданных уравнений движения – метод Бенеттина, который рассмотрен в предыдущем пункте (см. раздел 4.3.1). В матричных методах используются те или иные аппроксимации матрицы , с помощью которой по значению вектора рассчитывается следующее значение вектора . Оно и используется для вычисления оценок показателей Ляпунова.

Суть методики проста, но аппроксимация уравнений движения включает большое количество параметров, оказывающих значительное влияние на результаты вычислений показателей Ляпунова. Это обстоятельство затрудняет практическую реализацию методов.

У. Парлитц предложил идею уточнения истинных показателей Ляпунова при варьировании параметров, которая основана на том, что при обращении времени, показатели Ляпунова меняют знак, оставаясь теми же самыми по абсолютной величине. Поэтому, обрабатывая временной ряд от начала к концу, а затем от конца к началу, можно при сопоставлении результатов уточнить оценки.

Метод аналога связан с непосредственным вычислением скорости расходимости близких траекторий. В методе предлагается построить «синтетическую» траекторию из отдельных кусочков, имеющихся в наличии. Будем обозначать основную траекторию , а «соседние» траектории через , соответственно, . Обозначим  – длину вектора . В момент времени выбираем одну из соседних траекторий и полагаем . В некоторый момент времени норма становится слишком велика. Выбранную соседнюю траекторию больше нельзя считать близкой. В этот момент времени производится смена соседа. Для «старой» длины будем писать , а для «новой» –  . Значение выбирается так, чтобы направления векторов и были как можно ближе друг к другу. Далее до некоторого времени полагаем . Затем снова производим смену соседней траектории и т. д. Спустя шагов в качестве оценки старшего показателя Ляпунова получаем

.

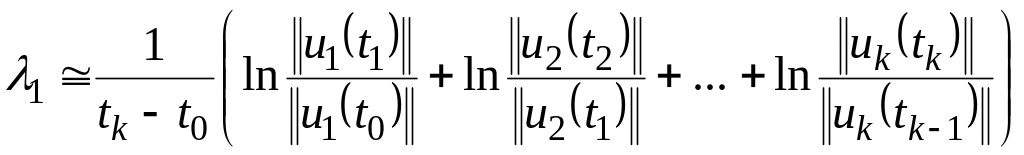Метод можно обобщить на  ‑ мерные фазовые объемы и вычислить сумму показателей, но уже при практическая реализация метода сталкивается с большими трудностями. Поэтому в подавляющем случае им пользуются только для оценки старшего показателя.

Метод обладает следующими достоинствами: очень малое количество подбираемых параметров – размер окрестности, максимальное удаление от траектории и допуск на угол между векторами при смене близкой траектории; независимость реализации метода от размерности пространства реконструкции.

Существует методика оценки старшего показателя Ляпунова, не требующая смены траектории. Методика использует двойное усреднение. Сначала определяется средний локальный коэффициент разбегания близких траекторий в данной точке

,

где усреднение проводится по всем ближайшим траекториям или по всем ближайшим соседям . Затем получают оценку старшего показателя Ляпунова

,

где усреднение выполняется по всем точкам .

Комбинированная методика или фрейм‑разложение. В алгоритме Бенеттина с помощью аппроксимации матрицы строится фазовый вектор, который используется для вычисления оценок показателей Ляпунова. Если не ставить цели расчета всех показателей Ляпунова, а ограничиться только старшим показателем, то можно построить вектор , не восстанавливая всю матрицу .

Пусть вычислен вектор вдоль траектории вплоть до точки . Рассмотрим ближайших соседей точки , т. е. точки . Образы ближайших соседей на следующем шаге также известны. Поэтому известен набор векторов , которые на следующем шаге отображаются в векторы . Именно по набору пар в матричных методах строится аппроксимация оператора .

Если можно было бы получить разложение вектора по этим векторам , то на следующем шаге мы могли бы вычислить вектор : . Т.е. вместо матрицы можно попытаться получить набор коэффициентов . Разложение должно быть выполнено по системе линейно‑зависимых векторов . В теории вейвлет-преобразований системы линейно‑зависимых векторов получили название фреймов, поэтому данный метод назван методом фрейм‑разложения.

Пусть задано несколько векторов и ляпуновский вектор . Будем полагать, что , и искать разложение в виде . Тогда , где .

В реальных расчетах вектор может немного отклоняться от линейной оболочки . Поэтому разложение будем обозначать

. (4.9)

Подобное разложение не единственно, поэтому необходимы дополнительные условия. Строго говоря, надо решать следующую задачу: найти

при условии и, например, .

Это приводит к обобщенной задаче на собственные значения, что делает методику слишком сложной. Поэтому будем решать более простую задачу:

найти , такое что и .

Если , то решение этой задачи совпадает с предыдущим случаем. В противном случае решение будет пропорционально проекции на это подпространство. Далее его надо будет лишь перенормировать таким образом, чтобы . Однако второй подход оказывается существенно проще. Благодаря линейности условия по коэффициентам задача сводится к решению системы линейных уравнений, а не к задаче на собственные значения.

На коэффициенты разложения (4.9) накладываются следующие ограничения.

1. Угол между векторами и не должен быть больше . Этого можно добиться, например, выбирая , .

2.  – все “лишние” коэффициенты, для которых соответствующие вектора почти ортогональны , должны быть близки к нулю.

3. Чем дальше находится соседняя точка, т. е., чем больше длина вектора , тем меньший вклад должен вносить он в окончательный результат, поэтому выбираем .

Таким образом, наибольший вклад должны давать ближайшие вектора, имеющие то же направление, что и .

Запишем

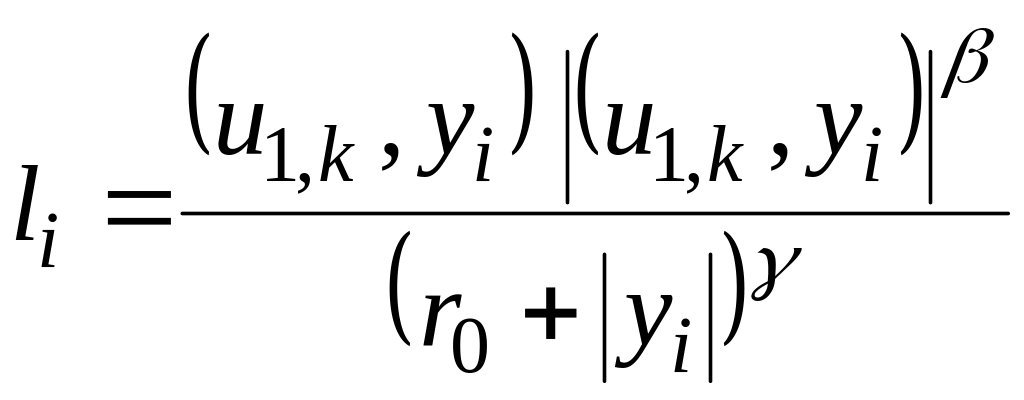, . (4.10)

Задачу на условный экстремум можно выразить следующим образом

,

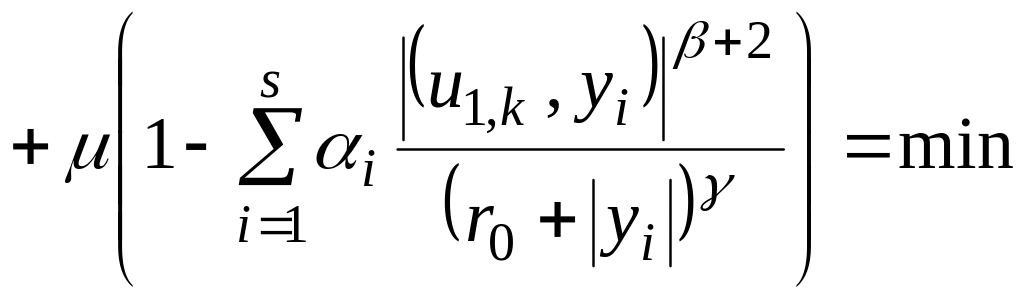где параметр обеспечивает равенство нулю тех коэффициентов , для которых . Далее получаем систему уравнений для

.

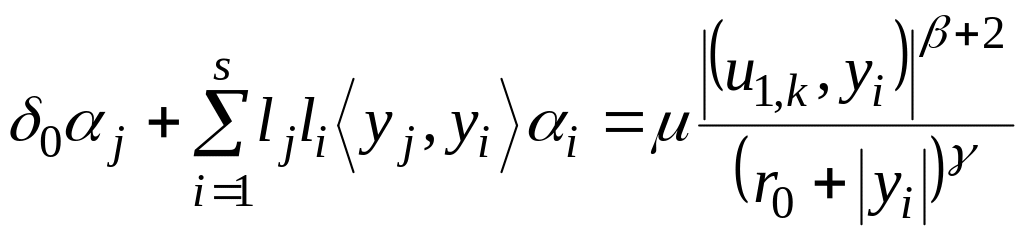Решая эту систему, находим отношение . Значение определяется по формуле (4.10) из условия нормировки .

Наличие нескольких методов расчета показателей Ляпунова принципиально важно. В реконструкции динамических систем по временному ряду могут возникать искажения, которые приводят к систематическим ошибкам в результатах. Разброс в значениях, которые получены разными алгоритмами при обработке одной и той же выборки, позволяет оценить реальную погрешность расчета, связанную с систематическими ошибками.

При расчете показателей Ляпунова по временным рядам следует придерживаться следующих рекомендаций.

Необходимо проводить расчет несколькими методами. Желательно одновременно провести расчет размерности аттрактора и энтропии при помощи корреляционного интеграла и сравнить со значениями, получающимися по значениям показателей Ляпунова.

Полезную информацию может давать расчет показателей для прямого и обращенного времени.

Желательно исследовать зависимость результатов от длины окна реконструкции. Это позволяет идентифицировать систематические ошибки, вносимые реконструкцией.

Достаточно надежный результат расчета показателей Ляпунова по временному ряду можно получить только как итог большой серии расчетов при помощи нескольких алгоритмов.