4.3. Спектр характеристических показателей ляпунова

Спектр характеристических показателей Ляпунова несет подробную информацию о качественном поведении системы. Аналитически показатели Ляпунова можно найти либо для простых аттракторов (неподвижная точка), либо для одномерных отображений. Для других случаев их рассчитывают численно. Спектр характеристических показателей можно вычислить двумя принципиально различными путями. Один основывается на вычислении траекторий, соответствующих линеаризованным уравнениям динамической системы, другой – на обработке значений временного ряда, полученного для выходных переменных динамической системы. Для качественного анализа динамики, включая и нерегулярную динамику, важны не столько абсолютные значения характеристических показателей, сколько их сигнатура. Возможность оценки только знаков характеристических показателей значительно упрощает вычислительную задачу.

Расчет показателей Ляпунова позволяет, например, вычислить горизонт предсказуемости , определяющий “среднее” время, втечение которого можно предсказывать поведение системы на аттракторе, и частоту измерения состояний системы при её мониторинге.

4.3.1. Вычисление спектра по уравнениям динамической системы

При численных расчетах, как правило, можно найти только «типичные» значения величин. Например, если численно решать линеаризованную систему дифференциальных уравнений, соответствующую исходной нелинейной системе, то из‑за ошибок округления практически всегда будет получаться значение показателя . Однако, типичным значением для старшего показателя ‑го порядка будет сумма наибольших показателей Ляпунова. Для численного расчета нескольких показателей используют эволюцию фазовых объемов. При таком подходе можно рассчитать любое количество показателей – от до .

Чтобы задать ‑мерный фазовый объем, необходимо линейно независимых решений линеаризованной системы

. (4.5)

Обычно начальные данные выбираются ортонормированными, что гарантирует линейную независимость. Далее проводится интегрирование системы (4.5), находится  ‑ мерный фазовый объем по формуле

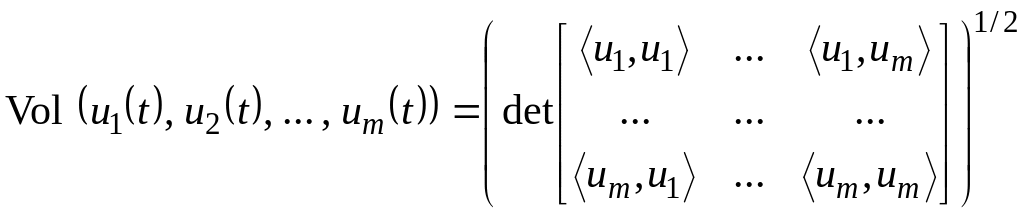
и вычисляется величина характеристического показателя  ‑ го порядка

.

Если значение этой величины останавливается с ростом времени, его можно принять в качестве оценки обобщенного показателя Ляпунова и тогда .

Однако этот простой подход оказывается неработоспособным по двум причинам.

1. Произвольно выбранные начальные данные обычно содержат ненулевую компоненту в направлении наибольшего растяжения , а если нет, то она обычно возникает в ходе расчетов из-за ошибок округления. Поскольку эта компонента растет, как , спустя некоторое время она станет доминирующей, все векторов развернутся в направлении и станут практически коллинеарными. После этого расчет образуемого ими объема станет невозможен из‑за конечной точности представления данных в ЭВМ.

2. Сама величина может за сравнительно небольшое время выйти за пределы машинной точности. Обычно это время существенно меньше, чем время, требуемое для расчета показателя Ляпунова.

Таким образом, необходима борьба с коллинеарностью векторов и выходом за пределы машинной точности.

Первая проблема решается при помощи процедуры ортогонализации векторов , т. е. перехода к новой системе решений

,

, .

Уравнения относительно линейны, поэтому векторы также будут решениями. Ортогонализация не меняет значение объема = , и векторы образуют систему решений, отвечающую тем же самым значениям показателей Ляпунова . Спустя некоторое время ортогонализацию надо повторять. Для ортогонализованной системы решений фазовый объем равен

,

и каждое из решений будет “отвечать” за свой характеристический показатель Ляпунова . Норма решения пропорциональна .

Проблема переполнения решается при помощи запоминания текущего значения и нормализации .

Далее полагая , повторяем всю процедуру. Нормализация делает объем единичным, как в начальный момент, но не меняет направлений, а потому не меняет и приращения объема на следующем этапе расчета. После очередной ортогонализации надо добавить к следующее значение .

Полный алгоритм расчета показателей Ляпунова для отображения

и соответствующего ему линеаризованного уравнения

имеет следующий вид.

1. Задаем ортонормированных векторов , присваиваем , и , а также определяем шаг перенормировки (можно положить ). Предполагается, что точка принадлежит аттрактору.

2. Делаем итерацию отображений, т. е. находим , .

3. Проводим ортогонализацию системы векторов , получая векторы :

, (4.6)

, ,

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

, ,

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4. Увеличиваем на логарифм нормы соответствующего вектора:

, ;

увеличиваем : . В качестве текущей оценки показателя Ляпунова можно использовать

.

5. Нормируем систему векторов вида (4.6), получаем ортонормированный базис следующего шага

и заносим его снова в вектора : .

6. Повторяем пункты 2-5 нужное число раз ( ).

7. Получаем окончательную оценку показателя Ляпунова. В простейшем случае выбираем

или .

Для потока

(4.7)

и соответствующей ему линеаризованной системы

(4.8)

алгоритм остается тем же самым за исключением следующих моментов.

1. Вместо итераций отображений решаются дифференциальные уравнения (4.7) и (4.8) на отрезке длины с начальными данными и . Далее в алгоритме вместо векторов используются векторы . Векторы будут определяться в точках .

2. При численной реализации алгоритма уравнения (4.7) и (4.8) следует решать совместно, объединив две эти системы в одну. Это связано с особенностями численных методов решения дифференциальных уравнений, реализованных в стандартных пакетах программ.

3. При аппроксимации уравнений (4.7) разностной схемой дифференциальные уравнения заменяются отображением , где  – шаг разностной схемы. В простейшем случае использования схемы Эйлера, это будет отображение . Результаты расчета показателей Ляпунова будут зависеть от выбранного шага разностной схемы, но при эта зависимость обычно исчезает.