3.5.6. Время предсказания

Энтропия также определяет среднее время, на котором можно предсказать состояние системы с динамическим хаосом. Например, для одномерного треугольного отображения, ограниченного единичным квадратом, после шагов по времени интервал вырастает до интервала . Если становится больше единицы, невозможно определить местоположение траектории на отрезке , и можно сказать лишь, что система с вероятностью находится на интервале , где  – инвариантная плотность системы. Другими словами, точное предсказание состояния этой системы возможно только на интервале времени , пока , т. е.

.

На временах, больших , возможны лишь статистические предсказания. Последнее уравнение можно обобщить на динамические системы размерности заменой характеристического показателя на энтропию

.

Величина обратная энтропии (при условии ее положительности) определяет характерное время перемешивания в системе. По прошествии промежутка времени начальная область фазового объема расплывается по всей энергетически доступной гиперповерхности (в отсутствие диссипации) или по предельному подмножеству фазового пространства – странному аттрактору (для диссипативных систем). При большом времени движения описание может быть только вероятностным. При малых временах поведение системы можно предсказать с достаточной точностью (не превышающей точность задания начального положения фазовой точки).

Таким образом, энтропия является важной характеристикой динамической системы и широко используется в качестве критерия хаотичности. Энтропия является мерой средней скорости потери информации о состоянии динамической системы с течением времени.

Энтропия для одномерных отображений равна показателю Ляпунова. Для систем большей размерности энтропия есть мера средней деформации ячейки фазового пространства и равна усредненной по фазовому пространству сумме положительных показателей Ляпунова.

Энтропия характеризует хаотическое движение, а странный аттрактор можно определить как аттрактор с положительной энтропией.

3.6. Автокорреляционная функция и спектральная плотность

Для выявления хаотических режимов наряду с характеристическими показателями Ляпунова и энтропией используются автокорреляционная функция и спектр мощности. Характер кривых, полученных при вычислении корреляционного интеграла и спектральной плотности, ­ один из самых простых и в то же время вполне надежных критериев, используемых для анализа режимов движения динамических систем.

3.6.1. Автокорреляционная функция

Для непрерывной системы автокорреляционная функция вводится как среднее по временному интервалу произведений , взятых в два различных момента времени и

.

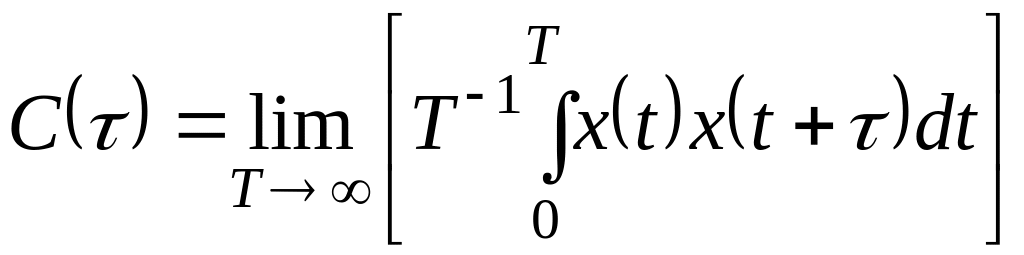Обозначим через итерации дискретной системы ,  – число итераций,  – начальное состояние.

Введем среднее (по числу итераций) значение

.

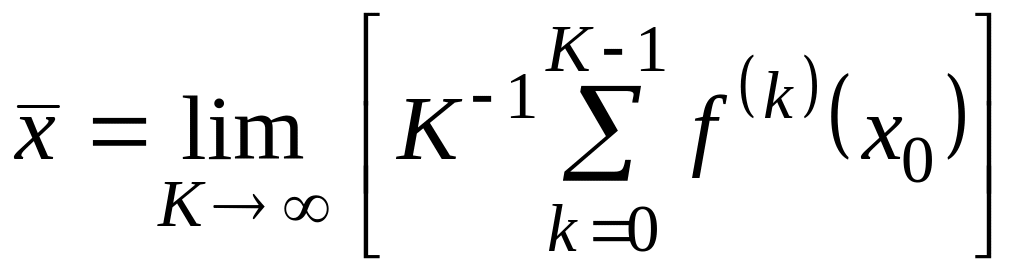Зная среднее значение , можно для каждой итерации найти ее отклонение от среднего значения . Рассмотрим две итерации, номера которых отличаются на величину

и .

Корреляционной (или автокорреляционной) функцией называется величина, определяемая пределом

.

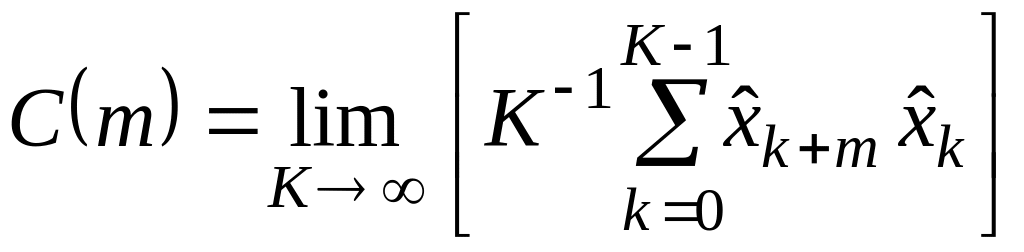Корреляционная функция показывает насколько отклонения от среднего значения , вычисленные через шагов (т. е. и ), связаны в среднем друг с другом. Если траектория хаотическая, то корреляция отсутствует, и функция спадает до нуля.

Если для данного отображения известна инвариантная мера, корреляционную функцию можно записать в следующем виде

.

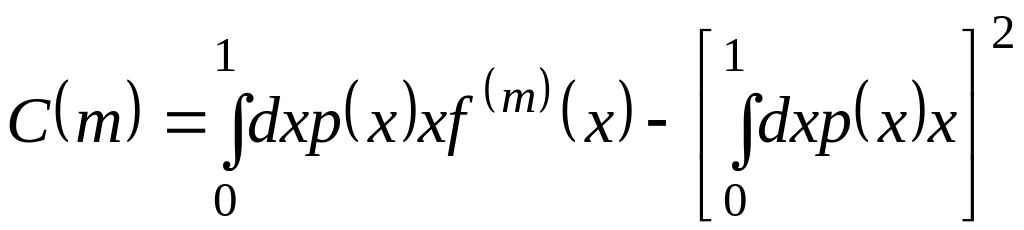Здесь использовано свойство коммутативности итераций

.

Последовательность для одномерного случая, может быть охарактеризована с помощью:

‑ показателя Ляпунова, который определяет скорость разбегания близких точек под действием отображения ;

‑ инвариантной плотностью вероятности, которая служит мерой того, как “плотно” точки итерационной последовательности распределяются на интервале;

‑ корреляционной функцией, которая измеряет зависимость между итерациями через шагов.

Пример. В случае треугольного отображения

, ,

для которого хаотическая последовательность равномерно покрывает единичный интервал, и инвариантная мера равна , для корреляционной функции имеем

,

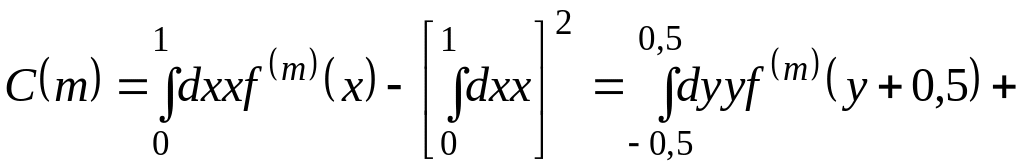
где  – дельта-функция Кронекера, равная нулю при несовпадающих значениях индексов. В случае треугольного отображения итерации коррелированны только при интервале корреляции , т. е. если номера итераций совпадают. Таким образом, последовательность итераций треугольного отображения дельта‑коррелирована.