4.7. Оценки энтропии

Обобщенный корреляционный интеграл был предложен как способ расчета энтропии Реньи для некоторого разбиения аттрактора на кубики, но затем разбиение было заменено на усредненную меру одного кубика. Зафиксируем масштаб разбиения и посмотрим, что получится, если увеличивать размерность реконструкции .

Пусть наблюдаемая величина изменяется в пределах от значения до значения . Разбиение отрезка на участки длиной порождает некоторое разбиение аттрактора в исходном фазовом пространстве на множества . Это будет множество всех векторов , для которых принадлежит ‑му отрезку. В простейшем случае, когда  – просто одна из компонент вектора , получится нарезка аттрактора гиперплоскостями на «ломтики». Теперь представим себе двумерную реконструкцию с разбиением на отрезки по обеим координатам вектора . Пусть некоторая точка попала в кубик . Это будет обозначать, что , а . То есть кубики будут отвечать разбиению «2‑го порядка» на множества , а «минус логарифм» корреляционного интеграла для него  – энтропии этого разбиения .

Рассуждая таким же образом, мы получим, что ‑мерная реконструкция будет соответствовать некоторому разбиению ‑го порядка, а корреляционный интеграл – давать значения . Тогда можно ожидать, что при малых разность или , когда . Напомним, что энтропия динамической системы отвечает свойствам отображения , а для отображения , которое отвечает временному шагу реконструкции аттрактора, соответствующее значение энтропии будет равно .

Строгого доказательства того, что корреляционный интеграл имеет отношение к энтропии, нет, но можно ожидать, что при малых значениях и достаточно больших будет выполнено

. (4.15)

Здесь использована длина окна реконструкции вместо , что удобнее. Фиксируя в формуле (4.15) масштаб и исследуя зависимость от величины , можно оценить энтропию динамической системы .

Соотношение (4.15) позволяет делать не только количественный, но и качественный вывод. Если система хаотична, то при увеличении график корреляционного интеграла должен проходить все ниже и ниже. По этому признаку можно иногда просто сделать вывод о хаотичности системы.

Алгоритм расчета энтропии . При алгоритм существенно упрощается. Перепишем соотношение (4.15) в виде

. (4.16)

Согласно известному определению корреляционного интеграла

.

Величину можно интерпретировать как вероятность того, что во множестве реконструированных векторов для случайно выбранной пары расстояние между ними будет не больше . Параметры реконструкции и при этом предполагаются фиксированными. Соотношение (4.16) означает, что в реконструкциях с большим значением должно быть очень мало близких пар. Действительно, для хаотических систем очень трудно найти два длинных куска временного ряда, которые повторяли бы друг друга с хорошей точностью.

Откажемся от последнего предположения и построим из одного и того же временного ряда много реконструкций для различных значений размерности : . Это будет отвечать значениям окна реконструкции . Будет ли соотношение (4.16) справедливо для такого «сводного» ансамбля векторов? При малых значениях и не слишком малых логично предположить, что будет. В таком случае можно уже приближенно рассматривать как совместную плотность вероятности, т. е. как вероятность того, что для данной пары векторов расстояние , а длина окна реконструкции равна .

Зафиксируем , тогда распределение пар векторов по длине окна при фиксированном расстоянии будет близко к экспоненциальному распределению . Среднее для такого распределения равно

.

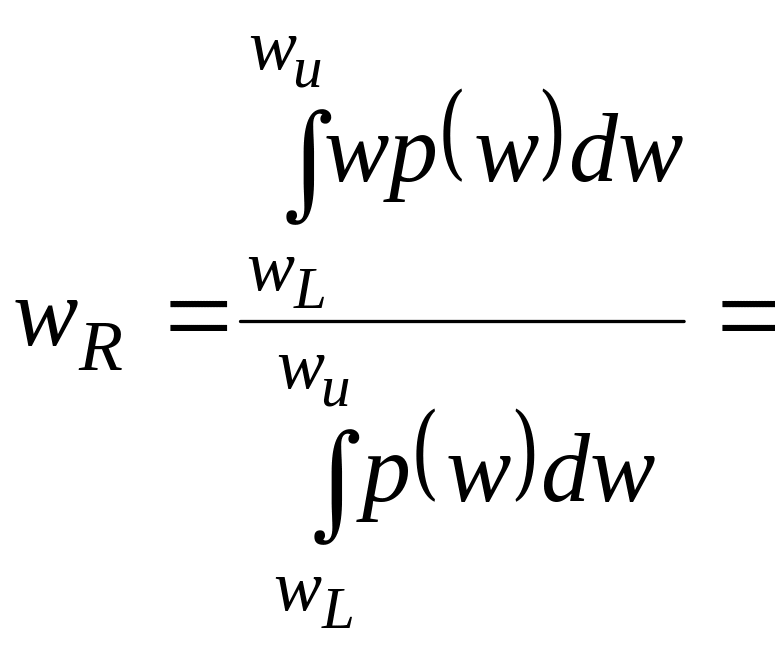
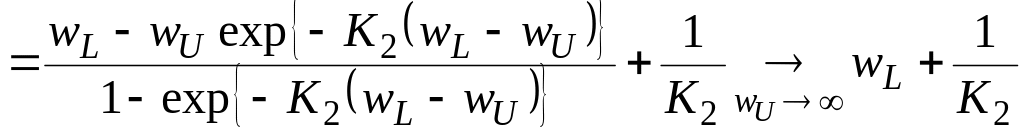Т. е., вычислив среднюю длину реконструкции для данного значения , мы получим величину, обратную энтропии. Достоинством метода будет то, что искомая величина вычисляется сразу, без дополнительных преобразований.

Корреляционный интеграл и статистические тесты. Предположим, что обрабатывается временной ряд чисто случайных величин , т. е.  – независимые и одинаково распределенные величины. Нам понадобятся свойства не самой величины , а случайной величины , которая служит основным материалом для расчета расстояний . Пусть случайные величины распределены с плотностью , а их функция распределения . Очевидно, что при . Для вычисления расстояний воспользуемся нормой (4.13). Тогда тот факт, что , означает, что одновременно должны выполнятся неравенства , . Поскольку входящие в эти неравенства  – независимые величины, то вероятность такого события, т. е. значение корреляционного интеграла равно

. (4.17)

Если плотность вероятности не имеет особенностей в нуле, т. е. при малых , то , а

, (4.18)

т. е. для таких плотностей размерность получающегося множества всегда равна размерности пространства реконструкции . Для других плотностей результат может оказаться иным, но нетрудно получить общее правило, если при , то значение размерности получится равным . Не столь важно велика эта оценка или мала, важно, что она монотонно возрастает с увеличением .

Этот результат и используется в качестве детектора некоррелированного или слабо коррелированного шума. Предположим, что исследуется временной ряд динамической системы невысокой размерности, к которому в процессе измерения добавился малый шум , т. е. данные имеют вид ,  – малый параметр. На масштабах влияние шума будет несущественно, и корреляционный интеграл получится почти таким же, как и в отсутствии шума. При малых масштабах данные будут выглядеть как случайные, и можно ожидать, что корреляционный интеграл будет похож на случай (4.18). Таким образом, на графике от должны быть две области: на больших масштабах при достаточно больших наклон стабилизируется, а на малых постоянно увеличивается с ростом . По такому поведению корреляционного интеграла можно установить наличие шума и примерно определить его амплитуду.

Иногда можно сделать более точные оценки. Рассмотрим поведение наклона корреляционного интеграла

.

Для данных с шумом на больших масштабах , а на малых, где сказывается влияние шума, . Функцию можно получить из рассчитанных значений корреляционного интеграла. Заметим, что для чисто случайных данных (4.18) . Если предположить, что данные сопровождаются гауссовым шумом с нулевым средним и неизвестной дисперсией, то значение дисперсии можно установить по полученной функции .

Данные для хаотической системы в случае короткой выборки можно принять за случайные. На графике корреляционного интеграла можно выделить два характерных масштаба: максимальное расстояние между точками и масштаб, начиная с которого график корреляционного интеграла становится почти линейным, и ниже которого можно исследовать фрактальные свойства . Очевидно, что , а на масштабах меньших должно быть справедливо соотношение (4.15), т. е.

.

Поэтому средний наклон на участке будет равен

,

т. е. будет линейно расти с увеличением . Если выборка недостаточно длинная, то масштабы, меньшие , могут оказаться неразрешимыми, и данные будут интерпретироваться как случайные. На самом деле это проявление искажений, характерных для реконструкции хаотических систем при слишком большой длине окна . Искажения связаны с искривлением и образованием складок, из-за которых реконструированный аттрактор на больших масштабах выглядит подобно скомканному листу бумаги.

Отметим еще одно использование корреляционного интеграла, связанное со случайными данными и статистикой. Для независимых случайных данных справедливо соотношение (4.17). По отклонениям от этого соотношения можно судить о зависимости или независимости данных друг от друга.