перекладывание отрезков, – бильярд Синая. Пусть  – многоугольник на плоскости с рациональными углами . Не ограничивая общности, можно считать, что все имеют вид

,

где и  – целые числа. Рассмотрим бильярд , при котором каждая траектория представляет собой ломаную линию, отражающуюся от границ по закону “угол падения равен углу отражения”. Тогда углы различных отрезков ломаной линии имеют вид

,

при некотором значении . Зафиксировав , мы получим инвариантное множество бильярда. Эргодические свойства бильярда на этом множестве сводятся к изучению эргодических свойств преобразования, действующего в пространстве отрезков, направленных под углами , и переводящего каждый отрезок в следующий отрезок вдоль траектории. Это преобразование можно реализовать как перекладывание отрезков.

3.5. Энтропия

Экспоненциальное увеличение расстояния между двумя первоначально близкими траекториями определяется характеристическими показателями Ляпунова. Скорость “расползания” большого количества бесконечно близких траекторий – энтропией динамической системы, которая является фундаментальной характеристикой степени случайности. Термодинамическая энтропия определяет меру беспорядка в системе. Рост беспорядка связан с ростом нашего незнания о состоянии системы. Энтропия – количество информации, необходимое для определения местоположения системы в некотором состоянии, т. е. мера незнания о системе.

3.5.1. Метрическая энтропия (энтропия Колмогорова–Синая)

Энтропию Колмогорова, которая связана со степенью хаотичности динамической системы, можно определить формулой Шеннона, так как энтропия пропорциональна скорости потери информации о состоянии системы с течением времени.

Рассмотрим траекторию динамической системы на странном аттракторе и предположим, что ‑мерное фазовое пространство разделено на ячейки размера . Состояние системы будем измерять через интервалы времени . Пусть  – совместная вероятность того, что траектория находится в ячейке с номером , траектория  – в ячейке с номером , … , траектория  – в ячейке с номером . По Шеннону, величина энтропии, определяемая формулой

,

пропорциональна информации, необходимой для определения местоположения системы на заданной траектории с точностью (если априори известны только вероятности ). Поэтому ( ) есть дополнительная информация, необходимая для предсказания, в какой ячейке окажется система в момент времени , если известно, что прежде она находилась в ячейках . Это означает, что ( ) описывает потерю информации о системе на интервале времени от до .

Определение 3.12. Энтропией Колмогорова (К‑энтропией) называется средняя скорость потери информации, определяемая пределом

. (3.29)

Предел , который берется после , делает величину энтропии независимой от частного вида разбиения фазового пространства. Рис. 3.7 иллюстрирует расчет величины К‑энтропии для одномерной динамической системы.

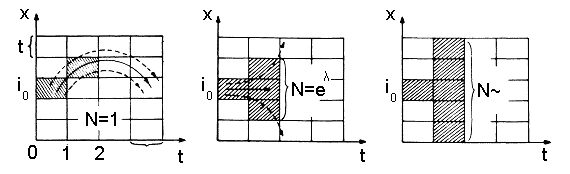
а) б) в)

Рис. 3.7. К‑энтропия одномерной динамической системы

Для регулярного движения первоначально близкие точки остаются близкими. Вероятность нахождения начальной точки траектории в ячейке равна . Совместная вероятность прохождения траекторией ячеек и равна , где  – количество ячеек, занимаемых траекторией в момент времени . Для регулярного движения (рис. 3.7. а) и энтропия .

Для хаотического движения первоначально близкие точки расходятся экспоненциально и , а , так как и энтропия положительна (рис. 3.7. б).

При случайном движении первоначально близкие траектории распределяются с равной вероятностью по всем возможным ячейкам: , (рис. 3.7в), и энтропия .

Таким образом, К‑энтропия может являться мерой хаоса: она равна нулю при регулярном движении, бесконечна для случайных систем, положительна и постоянна для систем с детерминированным хаосом.