5.3.3. Глобальные методы

К глобальным обычно относят те методы, в которых аппроксимация уравнений динамики осуществляется единой функцией во всей используемой области ‑пространства, т. е. сразу по всему множеству известных пар . Эти методы в первую очередь используются не для прогноза, а для анализа полученных уравнений движения или в случае необходимости глобальных идентификационных характеристик системы.

В качестве аппроксимирующей функции используются обычно многочлены. Коэффициенты многочлена находятся при минимизации полной ошибки

.

Методу присущи те же недостатки, что и локальной нелинейной аппроксимации, но устранить их еще труднее. Метод следует рассматривать скорее как статистическую модель.

При обработке временных рядов чаще используются методы, которые можно назвать глобальными аппроксимациями с локальными свойствами. К ним относится метод радиальных базовых функций.

Радиальные базовые функции. Для аппроксимации уравнений динамической системы выбирается точек-центров , которые могут и не совпадать с реконструированным вектором , и базовая или базисная функция одной переменной . Отображение строится в виде

.

Коэффициенты определяются из условия минимизации функционала ошибки

,

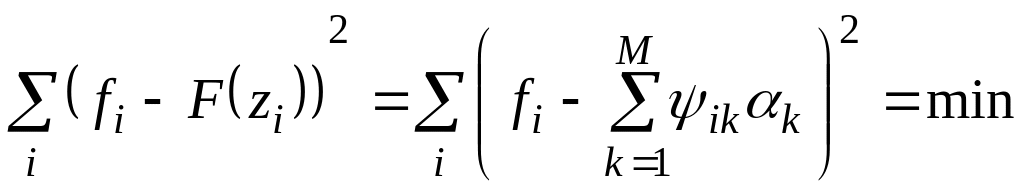где . В матричной форме это соотношение записывается в виде

.

Из последнего соотношения следует, что вектор коэффициентов является решением системы линейных уравнений

.

В ряде работ было показано, что для широкого класса функций матрица невырождена и, следовательно, метод реализуем.

Модификацией метода радиальных функций является метод ядер плотности – также статистическая модель. При этом функция используется для аппроксимации плотности вероятности и условной вероятности.

.

В качестве предсказания для следующего значения используется среднее значение по условной вероятности

.

В заключении следует отметить, что задача оценки параметров динамической системы по временному ряду в общем случае является некорректной. Отметим требования к динамической системе, при выполнении которых задача обработки становится корректной.

Свойства отображения . Теорема Такенса требует, чтобы отображение динамической системы было, по крайней мере, дважды непрерывно дифференцируемо. Кроме того, предполагается, что производные не просто непрерывны, но и «не слишком велики».

Особенности геометрической структуры аттрактора динамической системы и неоднородности инвариантной меры. Сравнительно редко посещаемые участки аттрактора могут вносить достаточно существенный вклад в измеряемые характеристики, чтобы сделать погрешность неприемлемо большой. При использовании алгоритмов нелинейной динамики, особенно оценок размерности, предполагается «однородность» свойств аттрактора, начиная с некоторого масштаба.

Длина выборки и точность измерений предполагается достаточной для применимости методов нелинейной динамики, в частности, реконструкции по Такенсу. Если характеристики при помощи некоторого функционала необходимо рассчитывать на масштабах , то необходимо, чтобы уровень шума был хотя бы в несколько раз меньше , а аттрактор должен быть заполнен точками с достаточной плотностью, чтобы расстояние до ближайшего соседа также было в несколько раз меньше .