3.5.2. Энтропия каскада
Дадим определение метрической энтропии (или энтропии Колмогорова–Синая) для дискретной системы. Пусть задан каскад
и его инвариантная
мера
на компактном носителе
.
В большинстве практически важных случаев
это физическая мера и аттрактор. Пусть
задано разбиение компактного носителя
на конечное число измеримых множеств
.
Обозначим множество точек, преобразуемых
во множество
,
отображением
,
как
.
Рассмотрим следующие разбиения,
порожденные таким “обратным”
отображением: на первом шаге разбиение
множества
;
на втором шаге разбиение на множества
,
т. е. – это
те точки из множества
,
которые на следующем шаге попадут в
множество
;
на третьем шаге разбиение на
,
т. е. те точки из множества
,
которые на следующих двух шагах попадут
сначала в
,
а затем в
;
и т. д.
Обозначим через
– диаметр
разбиения и вычислим энтропию каждого
разбиения
.
Определение 3.13. Энтропией дискретной динамической системы называется предел
,
т. е. асимптотическое
увеличение неопределенности для
разбиения бесконечно малого диаметра.
Иногда предел
сам по себе влечет измельчение разбиений,
тогда первый предел не нужен.
Определенная таким образом энтропия зависит от использованной меры. Если о мере ничего не говорится, то подразумевается физическая мера.
3.5.3. Обобщенная энтропия (энтропия Реньи)
Обычная, или шенноновская энтропия обладает одним замечательным свойством: если необходимо рассчитать суммарную энтропию двух независимых подсистем, то она будет равна сумме энтропий каждой из них.
Однако если
отказаться от этого свойства, то можно
ввести и другие меры неопределенности
состояния – энтропии
Реньи
порядка
:
,
.
При
энтропия Реньи стремится к обычной
шенноновской энтропии. Положим
,
.
Тогда
,
.
3.5.4. Топологическая энтропия
Предположим, что
мы можем различать точки фазового
пространства, отстоящие друг от друга
на расстояние, превышающее некоторую
величину
.
Рассмотрим пучок траекторий, выходящих
из окрестности начальной точки радиуса
,
т. е. в начальный момент не различимых.
Число различимых траекторий в некоторый
момент времени
обозначим
.
Топологической энтропией называется
величина
,
которая характеризует
степень разбегания близких фазовых
траекторий. Если траектории со временем
не разбегаются, либо разбегаются
недостаточно сильно (например, по
степенному закону), то энтропия
.
В противном случае, энтропия
.
Покроем аттрактор
динамической системы кубиками с ребрами
.
Пусть число этих кубиков равно
.
Обозначим
‑ й
кубик символом
.
Вероятность нахождения изображающей
точки в кубике
равна
,
где
– предельная
плотность вероятностей.
Согласно Шеннону энтропия системы равна
.
Величина
характеризует неопределенность
нахождения изображающей точки в кубиках
.
При измельчении покрытия значение
энтропии неограниченно возрастает.
3.5.5. Связь энтропии с характеристическими показателями Ляпунова
Для одномерных
отображений энтропия совпадает с
характеристическим показателем Ляпунова.
Двумерное отображение преобразует
окружность диаметра
в эллипс с осями
и
(рис. 3.8).
Отметим, что отрицательный характеристический показатель Ляпунова не вносит вклад в величину энтропии, так как не приводит к заполнению новых ячеек с течением времени. Энтропия определяется только положительным показателем Ляпунова. Для систем большей размерности скорость потери информации о системе (энтропия) равна средней сумме положительных показателей Ляпунова
.
Здесь суммирование производится по всем положительным показателям Ляпунова, а интеграл берется по некоторой инвариантной области фазового пространства.
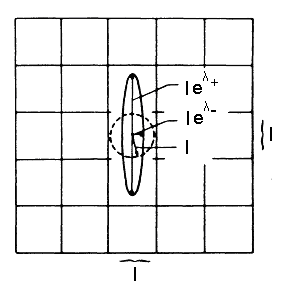
Рис. 3.8. Преобразование окружности
двумерным отображением
Энтропия понимается
как некоторая характеристика одной
стохастической компоненты движения. В
этом случае характеристический показатель
не зависит от траектории
,
и интеграл по множеству
равен единице. Отсюда энтропия равна
.