13. Расчет прочности изгибаемых элементов по нормальным сечениям. Элементы прямоугольного сечения с двойной арматурой

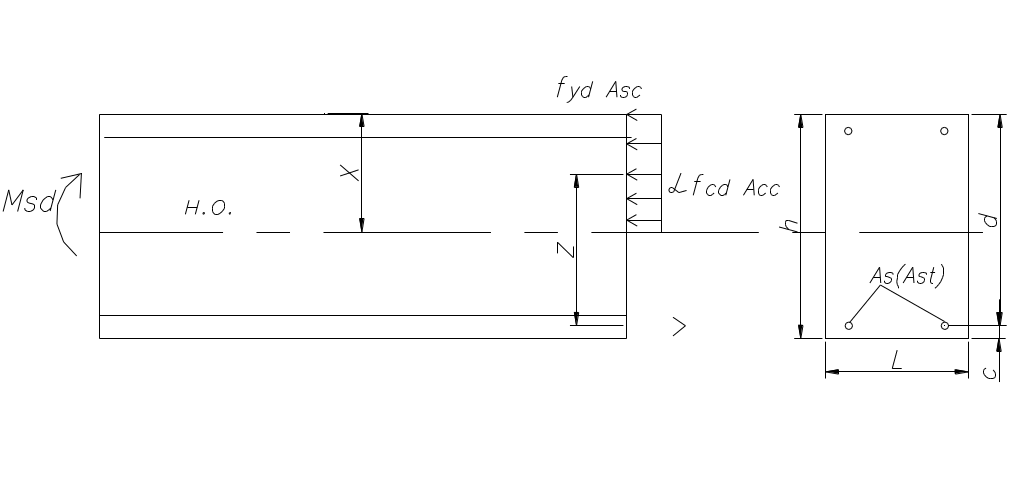
Асс = b*x – площадь сжатого бетона.

Расчет ведем из условия Msd≤Mrd

1)рабочая высота d=h-c; 2)коэффициент =Msd/α fcd b d² <1; 3)относительная высота сжатой зоны:ξ= Кс=0,85-для тяжелого бетона; Кс=0,8- для легкого бетона; σs,lim-напряжение в арматуре всех классов S240, S400, равное расчетному знач-ию fyd; = , -предельное напряжение в арм-ре сжатой части б-на, =500МПа. При ξ> - двойное армирование, приравниваем ξ= ; высота сжатой зоны x=ξ d; 5)определяем требуемую площадь сечения жатой зоны: A_sc^тр= . A_sc^тр≥A_s,min=0.002bd; 6)по сортаменту выбираем число сжатых стержней A_sc; 7)определяем требуемую площадь растянутой арматуры A_sc^тр= ; 8) по сортаменту назначаем число и диаметр арматуры, выписываем площадь Ast; 9)уточняем расстояние до центра тяжести с_ут и рабочую высоту d_ут; 10)уточняем высоту сжатой зоны: x_ут= ; 11)несущая способность: Mrd= , Mrd>Msd

14. Расчет наклонных сечений ж.б.эл-тов по поперечной силе. Прочность по наклон.трещине счит-ся обеспеч-й, если , ; - попереч. усилие, воспринимаем-е б-ном над вершиной наклон. трещины; - попереч.усилие,восприним-е попереч.стержнями пересек-ми опасн.наклон.трещину. ; - попереч.усилие,восприним-е наклон.стержнями, пересек.наклон.трещину .

S-шаг попереч.стержней(шаг хамутов) ; ; ; ; ; ; ; ; ; ; ; .Для исключения образования трещин между хомутами ограничиваем их шаг. ; , S . Подбор хамутов производят методом последоват.приближений:1)задаются d арм-ры из условий сварки ее с продол.стержнями,опред-м шаг попереч.стержней и получ.шаг сравнивают с мах допустимым и с шагом стержней по конструктив.треб-ям.2) По конструктив.треб-ям задаемся шагом попереч.стержней, зная шаг опред.требуем.диаметр попереч.стержней. При расчете конструкций с поперечной арматурой должна обеспечиваться прочность по наклонной полосе между наклонными трещинами: , , ; ; αe=Es/Ecm – модуль упругости арматуры и бетона соответственно.

15. Расчет прочности внецентренно сжатых элементов. Случай симметричного армирования.

Внецентренно сжатые конструкции – это конструкции в которых сжимающая сила приложена с эксцентриситетом, либо одновременна приложена сила и изгибающий момент.у=M/N.

Различают два случая при расчете:

1) большого эксцентриситета x_eff/d≤ξ_lim

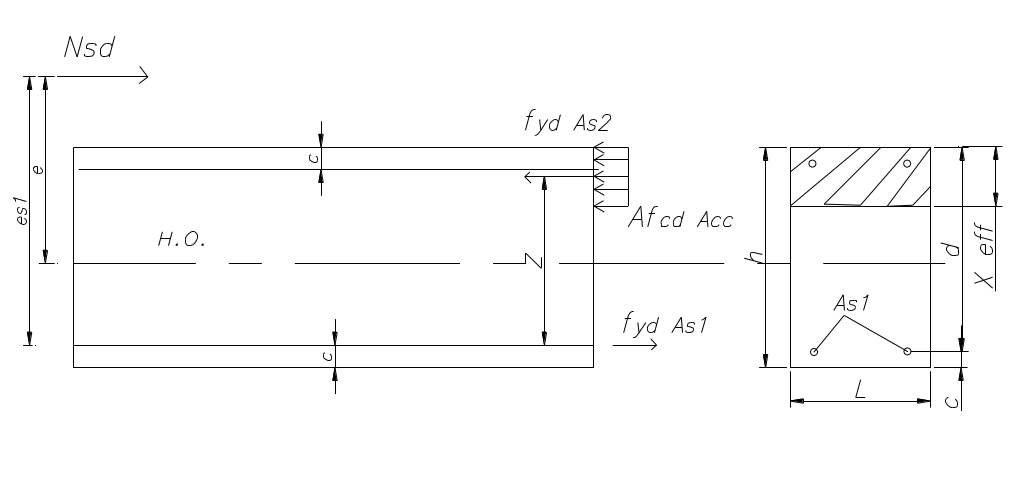
Расчет ведем из условия Mrd>Msd. Msd=Nsd e_s1, высота сжатой зоны определяется из равновесия: Nsd+f_yd A_s1-A_s2 f_yd=αf_cdA_cc.

2)малого эксцентриситета:

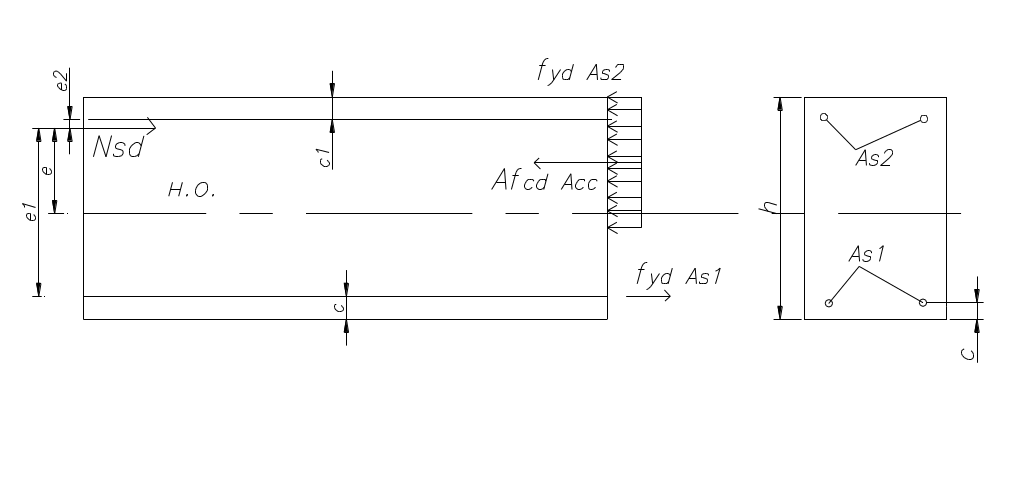
Mrd>Msd., : Nsd+ s As1-A_s2 f_yd=αf_cdA_cc, _s – направление в растянутой арматуре.

16. Расчёт прочности центрально и внецентренно растянутых элементов.

Расчёт прочности центрально растянутых элементов

Разрушение центрально – растянутых элементов происходит после того, как в бетоне образуются сквозные трещины и он в этих местах выключается из работы, а в арматуре напряжения достигают предела текучести (если сталь имеет площадку текучести) или временного сопротивления. Несущая способность центрально – растянутого элемента обусловлена предельным сопротивлением арматуры без участия бетона.

Трещины не образуются, если N≤N_cre, где N – внешняя нагрузка, N_cre – усилие, которое может воспринять сечение при образовании трещин. Для элементов без предварительного напряжения .

Для преднапряжённых элементов ,

где P – усилие предварительного обжатия, которое на стадии эксплуатации определяется с учётом всех первых потерь.

Расчёт прочности внецентренно растянутых элементов.

Предельное состояние по несущей способности элемента любого симметричного сечения, внецентренно растянутых в плоскости симметрии, характеризуется тем, что бетон пересечён сквозными трещинами, внешнему усилию сопротивляется лишь продольная арматура. Разрушение элемента наступает, когда напряжение в продольной арматуре достигают предельного значения. Расчёт производится из условия M_r≤M_cre,

где M_r – момент внешних сил, расположенных по одну сторону от рассматриваемого сечения относительно оси параллельной нулевой линии и проходящей через точку ядра сечения наиболее удалённую от растянутой зоны. ,

где e₀ – эксцентриситет внешних сил относительно центра тяжести приведенного сечения, r – расстояние от центра тяжести до самой удалённой точки ядра сечения в растянутой зоне, M_cre – сумма моментов всех внешних сил при образовании трещины.

, ,

где W_pl – пластический момент сопротивления, ; y=1,75 для прямоугольного сечения и таврового с полкой в сжатой зоне. ,

M_rp – момент обжатия силы Р в точке наиболее удалённой от растянутой зоны.