2.1.1. Перетворення Фур'є

Так називається дія, за допомогою якого по заданій в інтервалі функції будується система чисел (2.1.2). За традицією, саме ці числа також позначають словами «перетворення Фур'є» даної функції. При цьому числа називаються косинус- перетворенням Фур'є функції , а числа називаються синусом-перетворенням Фур'є функції . У перетворення Фур'є функції є множина властивостей і застосувань; зокрема,

відомий ряд прикладних питань, у яких ту або іншу інформацію про функцію вдається одержати тільки через її перетворення Фур'є, що у таких ситуаціях вдається одержати деякими непрямими засобами.

Розглянемо наступний окремий випадок. Функція розглядається на інтервалі

(-p ,p ) і притім тільки в його окремих точках

при деякому заздалегідь заданому й фіксованому числі . Значення функції в цих крапках уважаються відомими; позначимо

.

У рівності

=

покладемо . Одержимо

(2.2.1) .

Проаналізуємо співвідношення (2.2.1). Якщо довільне ціле ненегативне число розділити з остачею на число , то вийде співвідношення , де для цілих є лише наступні можливості:

.

З урахуванням періодичності косинуса й синуса у вираженні (2.2.1) можна привести подібні члени, у результаті чого вийде:

(2.2.2) ,

де

,

Відзначимо, що тепер всі суми в (2.2.2) - кінцеві. Відомий наступний факт про тригонометричні суми:

для всіх чисел мають місце рівності

Якщо обидві частини співвідношення (2.2.2) помножити на й потім просумировать по , те, з обліком тільки що сказаного, легко одержати, що

(2.2.3а) ;

а якщо обидві частини (7.2.2) помножити на й, з обліком того ж твердження про підсумовування косинусів і синусів, одержимо співвідношення

(2.2.3б)

причому в (2.2.3а) і (2.2.3б) . Числа , називаються дискретним перетворенням Фур'є функції . Якщо в рівності (2.2.2) замінити на довільний , то воно з точного стане наближеним. Його праву частину в цьому випадку називають тригонометричною інтерполяцією функції .

2.2. Зворотна матриця

Нехай А и В - дві матриці наступного виду:

і ;

оборотний увага на те, що в першій з них стовпців стільки ж, скільки в другий з них - рядків. У цьому випадку можна побудувати нову матрицю З

,

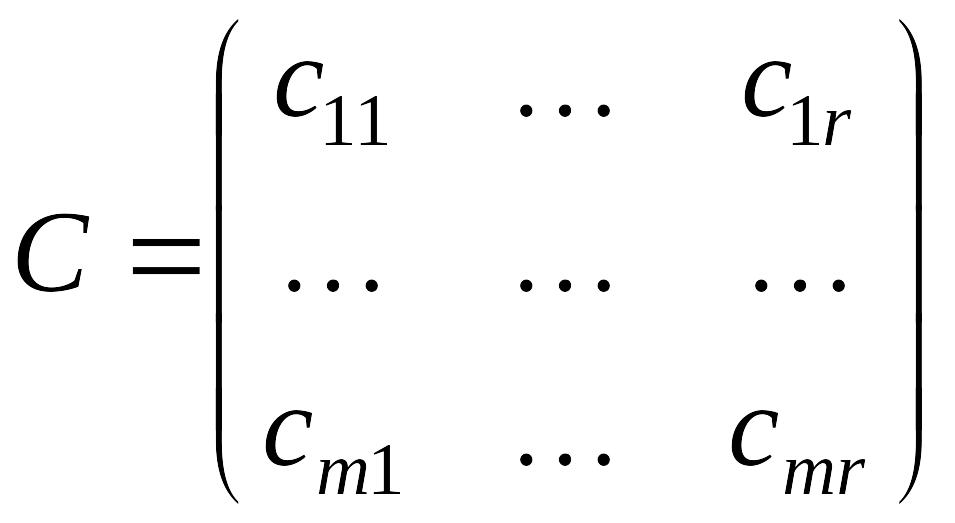називану добутком А на В (пишуть ІЗ=АВ), за правилом

,

де i=1,...,m і j=1,...,r. Серед матриць прийнято виділяти й позначати буквою E

наступну матрицю, називану одиничної, -

;

пояснимо: одинична матриця завжди квадратна, по її діагоналі коштує 1, а всі інші елементи - нулі, тобто якщо Е=(е_ij), i,j=1,...,n, те

.

Говорять, що квадратна матриця А и квадратна матриця В того ж розміру є зворотними по відношенню друг до друга, якщо виконано хоч одне з матричних рівностей - або АВ=Е або ВА=Е. Можна перевірити, що якщо одне із цих матричних рівностей виконується, то виконується й інше. Про всякий випадок пояснимо, що слова «матрична рівність» означають рівність заелементне, тобто якщо має місце рівність матриць U=V, те це означає, що в них рівні кількості рядків і рівні кількості стовпців і при цьому u_ij=v_ij для всіх i і j. Зокрема, система лінійних алгебраїчних рівнянь із п.3 Лекції 1 може бути записана у вигляді AX=B, де

,

а А и В мають той же змив, що й у п.3 Лекції 1.

Неважко помітити, що якщо для квадратної матриці А потрібно знайти зворотну матрицю В, те треба вирішити n систем лінійних алгебраїчних рівнянь із однієї й тої ж матрицею: запишемо матричну рівність АВ=Е поелементно (тут усього вийде n² рівностей), причому будемо послідовно дорівнювати стовпці - перший стовпець лівої частини до першого стовпця правої частини, другий стовпець лівої частини до другого стовпця правої частини й т.д. –

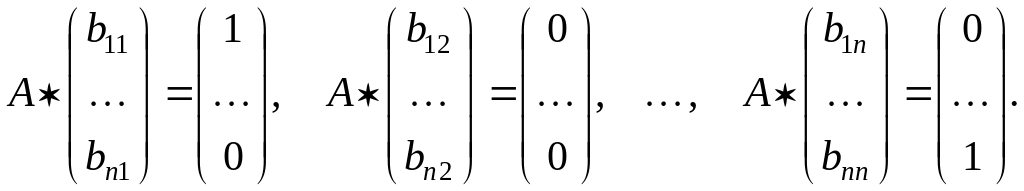
Із цього спостереження треба, що знайти зворотну матрицю можна вирішуючи одночасно n систем лінійних алгебраїчних рівнянь із однієї й тією же матрицею А.

Лекция 3

АЛГОРИТМИ ТА ПРОГРАМИ РОЗРАХУНКІВ ЗА ФОРМУЛАМИ ТА ТАБЛИЦЯМИ. ВИКОРИСТАННЯ ЛАНЦЮГОВИХ ДРОБІВ. СХЕМА ГОРНЕРА. МЕТОДИ ДІЛЕННЯ ВІДРІЗКА НАВПІЛ, ХОРД І ДОТИЧНИХ ДЛЯ УТОЧНЕННЯ КОРЕНЯ РІВНЯННЯ. ВІДШУКАННЯ РЕЧОВИННИХ КОРНІЙ АЛГЕБРАЇЧНИХ РІВНЯНЬ.